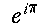
|
e^{i\pi} |
As in LaTeX, the carat (^) is used for superscripts and
the underscore (_) is used for subscripts. In general,
curly braces should be put around the raised or lowered expression.
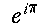
|
e^{i\pi} |
If the superscript or subscript consists only of a single character, the braces are not necessary.
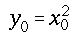
|
y_0 = x_0^2 |
WebTeX can display tensor notation with the \tensor{}{}
command. The first argument is the base, and the second argument
contains a series of subscripts and superscripts marked with _ and ^.
Pairs of ^ and _ are matched from left to right and aligned in the
same column, regardless of
order within the pair. If a ^ does not pair up with a _ when the pairs
are made, then the missing subscript is
left blank. In the example \tensor{R}{_i_k^j^m} below,
the first subscript can not be paired up with a superscript, so the
superscript's spot above the 'i' is blank. The same
thing happens with the last superscript 'm'.

|
\tensor{R}{_i^j_k} |
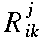
|
\tensor{R}{^j_i_k} |
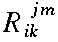
|
\tensor{R}{_i_k^j^m} |
The WebTeX Examples include more examples of superscripts and subscripts, as well as an example of tensor notation.
Superscripts and subscripts may also be placed before an expression. These can be created
with the \multiscripts{}{}{} command, a generalization of \tensor.
Here, the second argument is the base, while the first argument contains the prescripts and
the third argument contains the postscripts. These scripts are defined (by pairing up ^
and _) in the same way as they are for \tensor.
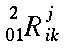
|
\multiscripts{_0^2_1}{R}{_i^j_k} |
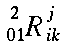
|
\multiscripts{^2_0_1}{R}{^j_i_k} |
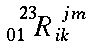
|
\multiscripts{_0_1^2^3}{R}{_i_k^j^m} |
The WebTeX Examples include an example of prescripts.
Fractions may be created with \frac by placing the
numerator in the first argument and the denominator in the second
argument.
"One over x" is created with
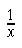
|
\frac{1}{x} |
The command \binom is similar to \frac.
It places the first argument over the second argument, without
drawing the horizontal fraction bar. To create a binomial coefficient,
you will need to add parentheses with the \left ( and
\right )commands. See the section on delimiters
for further discussion of \left and \right.

|
\left ( \binom{5}{2} \right ) |
The WebTeX Examples include more examples of fractions.
The command \sqrt displays the square root of its
argument.
For the n-th root, use the command \root with
n as the first argument and the expression under the
radical as the second argument.
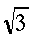 |
\sqrt{3} |
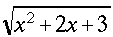
|
\sqrt{x^2+2x+3} |
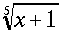 |
\root{5}{x+1} |
The WebTeX Examples include more examples of roots.
Some symbols will be larger in display style than they are in text style. These are
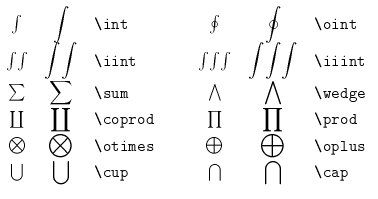
Upper and lower limits for integrals or other variable size symbols can be
specified with ^ and _ respectively. In
display mode, these limits will be above and below the integral
symbol. In text mode, the limits will be placed to the right of the
symbol.
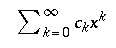
|
\textstyle{ \sum_{k=0}^{\infty} c_k x^k } |
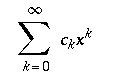 |
\displaystyle{ \sum_{k=0}^{\infty} c_k x^k } |
\iint draws a double
integral, and \iiint
draws a triple integral. These draw the integral symbols closer
together than they normally would get with
\int \int or
\int \int \int.
Use \displaystyle
{\cup} to force the cup symbol to be large when the surrounding
expressions are otherwise in text style.
The following five symbols will be large, regardless of the current style:
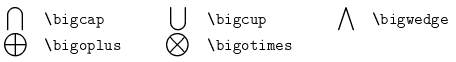
The WebTeX Examples include examples of an integral in display style and variable-sized symbols.
Many functions are traditionally typeset in an upright font. The following WebTeX commands automatically have this property.
\arccos \cos \csc \exp \ker \limsup \min \sinh \arcsin \cosh \deg \gcd \lg \ln \Pr \sup \arctan \cot \det \hom \lim \log \sec \tan \arg \coth \dim \inf \liminf \max \sin \tanhThe limit functions will deal with subscripts and superscripts in a manner similar to the operators in the previous section. In display style,
\lim_{x \to 0} f(x) will place the subscript
underneath the limit symbol.

|
\textstyle{\lim_{x \to 0} f(x)} |
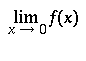 |
\displaystyle{\lim_{x \to 0} f(x)} |
If you have a function that is not on the list above, you may force any identifier to behave as an operator using the
\mathop{function}
command. For instance, the cosine function would normally be used this way:
\cos x
However, if the cosine function wasn't already on the list above, the command
\mathop{cos} x
The WebTeX Examples include an example of log-like functions.
Delimiters are the symbols such as parentheses and brackets which
enclose a mathematical expression. These symbols, when used with the
\left and \right commands, will grow to fit
the size of the expression they enclose. The delimiters which WebTeX
recognizes are:

Note that the curly braces must be specified with \{ and
\} since braces alone are interpreted by WebEQ as part of
the commands.
A simple example is

|
\left ( \frac{2}{4+x} \right )^3 |
The \left and \right commands must be used in pairs, since WebTeX
expects the expression that determines the height of the delimiters to
be surrounded by a pair of \left and \right commands. However, only
the \left and \right keywords must appear in pairs;
either delimiter after the keyword may be omitted:

|
\left \frac{x}{y} \right|_{x=0} |
Caution: This is a significant difference between WebTeX and
TeX. In TeX, some delimiter is required after the \right
or \left command and uses a special invisible delimiter
in situations like the one illustrated above.
By default, delimiters grow symmetrically around the horizontal axis of the
equation. When enclosing a matrix that is aligned at its top or bottom, for
example, one needs the delimiters to "float" to match the alignment of
the enclosed expression. To accomplish this, use the
\floatleft and
\floatright commands instead. For matching purposes, a
\floatleft
will match a plain \right and vice versa.
The WebTeX Examples include more examples of delimiters.
There are seven accents which place a one-character wide accent above their arguments:

The wide versions of these five accents stretch to the width of the enclosed expression.

|
\widehat{a+b} |
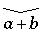
|
\widecheck{a+b} |
 |
\widebar{a+b} |
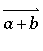 |
\widevec{a+b} |
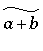 |
\widetilde{a+b} |
The WebTeX Examples include more examples of accents.
The command \overbrace places a horizontal brace that
stretches over its argument, and \underbrace stretches a brace
underneath its argument.
Besides braces, any symbol may be placed above or below an expression
with the commands \overset or \underset.
These are generalizations of \overbrace and
\underbrace. Instead of a brace, any symbols that are in
the first argument will be typeset above or below the main expression
in the second argument.
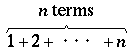
\overset{\text{$n$ terms}}{\overbrace{1+2+\cdots+n}}
The WebTeX Examples include more examples of the overbrace and overset commands.
There are many other mathematical symbols which are supported by WebTeX.
Both capital and lower-case Greek letters are available. The capital letters that are not listed on the table below are the same as the Roman capitals.
Capital letters:
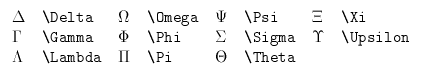
Lower-case letters:

Arrows:

Relations:

Binary operations:
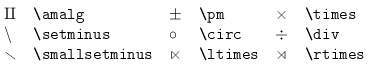
Dots:

Miscellaneous Symbols:


Created: Dec 18 1997 ---
Last modified: Tue Oct 23 17:24:20 2001
Copyright © 1997-2002 Design Science, Inc.
All rights reserved.