Musings

More AdS/QGP

As you can probably tell, I’m really rather enamoured of the application of AdS/CFT technology to study the properties of the quark-gluon plasma at RHIC (I, II, III). A lot of nuclear physicists (who are used to making various crude approximations in attempting to describe nuclear dynamics) are also quite excited.

In the AdS/CFT approach, one replaces finite-temperature QCD (in a strongly-coupled plasma phase) with some other (usually supersymmetric) gauge theory which, unlike QCD, is controlled by a nontrivial UV fixed point. So the microscopic degrees of freedom in the plasma are rather different from those of QCD. Moreover, calculations are done at large-$N_c$ and large $\lambda=g^2 N_c$ limit, whereas we are really interested in $N_c=3$, $\lambda\sim 20$. Still, if we are interested in hydrodynamic and finite-temperature transport properties, the precise microscopic degrees of freedom may not matter too much. And one can astutely study ratios of quantities in which one might expect the number of microscopic degrees of freedom to drop out. Moreover, one can test the robustness of the result by computing in different theories ($\mathcal{N}=4,\, \mathcal{N}=2^*,\dots$).

Still, one might be sceptical of the whole approach, were there some other approach to calculating transport coefficients in a strongly-coupled quark-gluon plasma. Unfortunately, for these purposes, AdS/CFT is the only game in town.

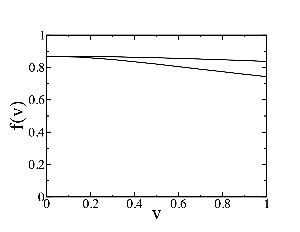
A plot of $f(v,\theta)$, showing both the mild dependence on $v$ and on $\theta$. The upper curve is for $\theta=\pi/2$; the lower curve is for $\theta=0$, with the behaviour for general $\theta$ interpolating between the two.

With that preamble, I thought I’d point to some of the latest interesting results in the subject. One important effect observed at RHIC is the suppression of J/Ψ production. The intuitive picture is that, when $c\overline{c}$ pair is produced in the collision, instead of forming a $c\overline{c}$ bound state, the potential between them is screened and, instead, they tend to form charmed mesons. The static heavy-quark potential is well-understood from lattice studies. And so are the corrections due to finite-temperature effects.

Unfortunately, the lattice calculations don’t tell the whole story, as they apply to static quarks, whereas the $c\overline{c}$ pairs at RHIC are produced with significant velocity, relative to the plasma. Experimentally, this appears to be important. So it’s interesting to study the velocity dependence of the screening length theoretically. Which is where AdS/CFT comes in.

Liu, Rajagopol and Wiedemann studied the problem in the $\mathcal{N}=4$ theory, where they obtained $$L_s(v,T) = \frac{f(v,\theta)}{\pi T} (1-v^2)^{1/4}$$ where $f(v,\theta)$ is a function that depends very mildly on the velocity of the $q\overline{q}$ dipole relative to the plasma and on its orientation, $\theta$, relative to its velocity.

$L_s(0,T)$ is off by about a factor of 2 from the lattice QCD results ($L_s\sim 0.5/T$ for 2 flavours of light quarks, and $L_s\sim 0.7/T$ without dynamical quarks). But that’s not an unexpected discrepancy, given the arguments above. What’s important (and, one hopes, more robust) is the velocity dependence $$L_s(v,T) \sim L_s(0,T) (1-v^2)^\xi$$ where, for the $\mathcal{N}=4$ theory, one has $\xi=1/4$.

Càceres, Natsuume and Okamura studied a series of other backgrounds, and argue that $\xi=1/4$ for conformal theories but that, systematically, $\xi\lt 1/4$ for non-conformal theories, like the Klebanov-Tseytlin cascade. Based on their examples, they conjecture a formula $$\xi = \tfrac{1}{4}- \tfrac{3}{16}\left(1-3c_s^2\right)$$ relating the exponent to the sound speed in the plasma. If such a relation holds, one would obtain $\xi\sim 0.22$ for the quark gluon plasma at RHIC.