The n-Category Café

Grothendieck’s approach to Galois theory makes heavy use of an analogy with covering spaces in topology, so let’s start there.

Covering spaces

Here is a covering space of the circle:

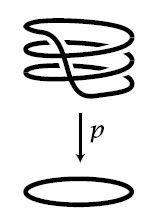
There are 4 points sitting over any point of the circle. So, if you stand anywhere on the circle, 4 guys could be standing directly above you, one at each of these points.

Suppose now that you play a game: as you walk around the circle, these guys have to follow you, staying directly overhead. If you walk all the way around the circle once, these guys switch places in a certain way. With this particular covering space they get cyclically permuted:

$$1 \mapsto 2$$ $$2 \mapsto 3$$ $$3 \mapsto 4$$ $$4 \mapsto 1$$

But you could play this sort of game with any covering space of the circle, and you’d get some permutation of some bunch of guys. Even better: for any permutation of any set of guys, we can cook up a covering space of the circle, such that when you play this game and walk once around the circle, the guys will carry out the desired permutation!

To formalize this, you can make up a category of covering spaces of the circle, and a category of ‘sets equipped with permutation’, and prove these categories are equivalent.

But there’s no need to limit yourself to the circle. Suppose you have a connected manifold $X$, and suppose you choose a point $x \in X$. Then you can go back and forth between covering spaces

$$p \colon E \to X$$

and actions of the fundamental group $\pi_1(X,x)$ on sets. The idea is that sitting over the point $x$ there is some set of points in $E$. That’s your set:

$$S = \{e \in E \vert \; p(e) = x \}$$

If you start at $x$ and walk around a loop in $X$ you can get little guys standing at these points to follow you overhead in $E$, and they’ll come back permuted. That’s how the fundamental group $\pi_1(X,\ast)$ acts on the set $S$. Conversely — and this takes a bit more work — given any set $S$ equipped with an action of $\pi_1(X,x)$, we can build a covering space $p \colon E \to X$.

We can formalize this result as an equivalence of categories. We could also generalize it. For example, we could drop the requirement that $X$ is connected, and avoid choosing a favorite point $x$, by replacing the fundamental group with the fundamental groupoid. There’s also no need for $X$ to be a manifold — though it does need to be nicer than an arbitrary topological space. To see all these things, try:

• nLab, Fundamental theorem of covering spaces.

But I want to do the opposite of generalizing: I want to limit myself to compact manifolds. Why? To bring in some finiteness conditions that we’ll see analogues of later, when we get to Galois theory.

If we require that our manifold $X$ and its covering space $E$ are compact, this forces our set

$$S = \{e \in E \vert \; p(e) = x \}$$

to be finite. Conversely if $X$ is compact and $S$ is finite, the covering space $E$ will be compact. So I believe we get this:

Theorem 9. Suppose $X$ is a connected compact manifold and $x \in X$. Then the the category of compact covering spaces of $X$ is equivalent to the category of finite sets equipped with an action of $\pi_1(X,x)$.

Furthermore, a covering space $E$ is connected iff the corresponding action of $\pi_1(X,x)$ is transitive. This a way of saying a guy up in $E$ can walk from any point over $x$ to any other point over $x$ by following me as I walk around some loop in $X$. So, we get

Theorem 10. Suppose $X$ is a connected compact manifold and $x \in X$. Then the category of connected compact covering spaces of $X$ is equivalent to the category of finite sets equipped with a transitive action of $\pi_1(X,x)$.

By the way, I’m carrying on the numbering of theorems from last time. And I’m mentioning these two results mainly as a warmup for two analogous results in Galois theory. Those are my destination today.

Galois theory

In algebraic geometry we learn that any commutative ring acts like a ring of functions on a kind of space called an affine scheme. You can click the link for the definition, but the upshot is that we can define the category of affine schemes, $\mathrm{AffSch}$, to be the opposite of the category of commutative rings, $\mathrm{CommRing}$. So the objects in these two categories are really the same, but we think about them differently.

We call the affine scheme associated to a commutative ring its spectrum, ultimately because the spectrum of light produced by a hot gas is an example. But never mind that now. All you need to know is this: any commutative ring $R$ gives an affine scheme called $\mathrm{Spec}(R)$, and any ring homomorphism

$$f \colon R \to S$$

corresponds to a map of affine schemes

$$\mathrm{Spec}(f) \colon \mathrm{Spec}(S) \to \mathsf{Spec}(R)$$

Now, with a lot more work we can define what it means for a map of affine schemes to be like a covering space, and we can copy Theorem 9 in this context. And we get the fundamental theorem of Grothendieck’s Galois theory!

To keep things as lowbrow as possible I want to talk about commutative rings than affine schemes. When a map of affine schemes

$$\mathrm{Spec}(f) \colon \mathrm{Spec}(S) \to \mathsf{Spec}(R)$$

is like a covering space, we say the ring homomorphism

$$f \colon R \to S$$

is ‘etale’. So the question is: when is a ring homomorphism etale?

The answer is simplest when $R$ is a field. In this case any homomorphism $f \colon R \to S$ is one-to-one, and $S$ becomes a commutative algebra over the field $R$. Then $f$ is etale iff $S$ is a separable commutative algebra over $R$.

Why is this true? That’s a very important question, which I want tackle someday. But first: you may be wondering what ‘separable’ means. I said a lot about separable algebras last time, but that was a long time ago, so let me remind you. Skip the next section if you remember.

Separable algebras

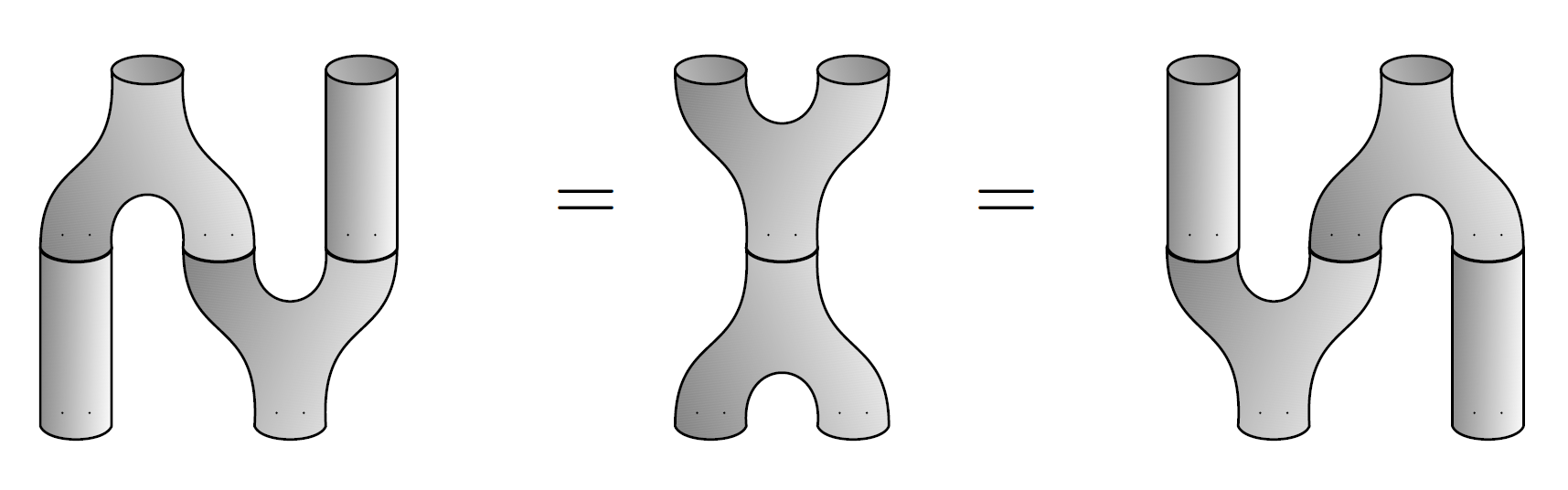
Let’s change notation now and let $A$ be any algebra over a field $k$. $A$ is separable if can be equipped with the structure of a special Frobenius algebra. Unpacking the jargon, this means we can find a map

$$\Delta \colon A \to A \otimes A$$

which has

$$\qquad \qquad m(\Delta(a)) = a \qquad \qquad \qquad \qquad (1)$$

and

$$\qquad a \Delta(b) = \Delta(a b) = \Delta(a) b \qquad \qquad (2)$$

In the first equation

$$\begin{array}{rccl} m \colon & A \otimes A &\to& A \\ & a \otimes b &\to& a b \end{array}$$

is the multiplication in $A$, and in the second I’m making $A \otimes A$ into an $(A,A)$-bimodule in the obvious way:

$$a(b \otimes c) = a b \otimes c, \qquad (b \otimes c) a = b \otimes c a$$

If we write the multiplication $m$ like this:

$\quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

and write the ‘comultiplication’ $\Delta$ like this:

$\quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

then equation (1), called the special law, says

$\quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

while equation (2), called the Frobenius laws, says

$\quad \qquad \qquad \qquad \qquad$

Separable field extensions

Last time I explained that when $k$ is an algebraically closed field, the only commutative separable algebras over $k$ are finite products

$$k \times \cdots \times k$$

Geometrically speaking, this says that the coverings of $\mathrm{Spec}(k)$ are quite boring. It’s like how a covering space of a point is just a bunch of points. But now let’s see what happens for fields that may not be algebraically closed.

Theorem 11. Any commutative separable algebra over a field $k$ is a finite product of finite separable extensions of $k$.

More buzzwords! And worse, the word ‘separable’ in the phrase ‘separable extension’ doesn’t mean the same thing as it does in the phrase ‘separable algebra’. They are related, and indeed the theorem says how. But I should explain.

An extension of a field $k$ is a field $K$ that contains $k$ as a subfield. When this happens $K$ will be a vector space over $k$, indeed an algebra. We say the extension is finite if $K$ is finite-dimensional as a vector space over $k$.

Suppose $K$ is any extension of $k$.

An element $x \in K$ is algebraic over $k$ if it obeys some polynomial equation with coefficients in $k$. For example, if $K$ is a finite extension of $k$ then every $x \in K$ is algebraic. Otherwise all the elements $1, x, x^2, \dots$ would be linearly independent over $k$, and $K$ would not be finite-dimensional!

If $x \in K$ is algebraic over $k$, there is a unique polynomial $P$ with coefficients in $k$ such that

• $P(x) = 0$,
• $P$ has the lowest possible degree for a nonzero polynomial that vanishes on $x$,
• the leading coefficient of $P$ is $1$.

This is called the minimal polynomial of $x$.

If $x \in K$ is algebraic over $k$, we say it’s separable if the derivative of its minimal polynomial is nonzero. And finally, we say the extension $K$ of $k$ is separable if all its elements are separable.

I don’t really like throwing piles of definitions at you like this. I want to explain separable field extensions more conceptually. However, today my main goal is to state the fundamental theorem of Grothendieck’s Galois theory — just to put it on the table. So, for now, I’ll only say a few reassuring words to the beginners out there.

First, saying an algebraic element of an extension of $k$ is separable is a bit like saying it’s ‘generic’: no weird coincidences are making the derivative of its minimal polynomial zero.

Second, it actually takes some work to find nonseparable finite extensions of a field! For a field of characteristic zero, or a finite field, all finite extensions are separable.

So, you can think of separable finite extensions of fields as the ‘easiest to understand, least annoying’ extensions. And Theorem 11 links them to separable commutative algebras in a very nice way. But this is not getting to the bottom of separability — not by a long shot.

Galois theory in a nutshell

Before diving into Grothendieck’s Galois theory we need to know a bit about ordinary Galois theory. I never took a course on Galois theory because it seemed dry and uninteresting at the time. As a youth I was interested in quarks and black holes, not why you can’t trisect a bloody angle using archaic tools! Now, in my old age, I am condemned not only to study Galois theory but to blog about it. I hope you’re not in the same boat. I hope you know all this stuff and understand it deeply.

Given a finite separable extension $K$ of a field $k$, we can form the group of automorphisms of $K$ that fix every element of $k$. This group is always finite. And when we’re lucky, only elements of $k$ are fixed by everything in this group. In this case we say $K$ is a Galois extension of $k$, and a bunch of nice things happen.

For starters, in this case we call the group of automorphisms of $K$ that fix every element of $k$ the Galois group $\mathrm{Gal}(K|k)$. But that’s not the main nice thing!

The first nice thing is that for any subgroup $G \subseteq \mathrm{Gal}(K|k)$, there’s a field $F$ consisting of all elements of $K$ fixed by everything in $G$. This field has

$$k \subseteq F \subseteq K$$

so we call it an intermediate field: intermediate between $k$ and $K$, that is.

Conversely, for any intermediate field $k \subseteq F \subseteq K$ we get a group $G \subseteq \mathrm{Gal}(K|k)$ consisting of precisely those elements that fix everything in $F$.

In fact, this sets up a one-to-correspondence between subgroups

$$G \subseteq \mathrm{Gal}(K|k)$$

and intermediate fields with

$$k \subseteq F \subseteq K$$

Bigger subgroups $G$ correspond to smaller intermediate fields $F$. Furthermore, normal subgroups $G \subseteq \mathrm{Gal}(K|k)$ correspond to fields $k \subseteq F \subseteq K$ that are Galois extensions of $k$. Even bettter, if $G$ is normal then the corresponding intermediate field $F$ has

$$\mathrm{Gal}(F|k) \cong \mathrm{Gal}(K|k) / G$$

The analogy between covering spaces and Galois theory

Everything I just said about Galois theory has an analogue for covering spaces. Thanks to stuff I already said, if $K$ is a finite separable extension of $k$ then the inclusion

$$i \colon k \to K$$

gives an etale map

$$\mathrm{Spec}(i) \colon \mathrm{Spec}(K) \to \mathrm{Spec}(k)$$

and we should think of this as a covering space. It will always be a connected covering space with finitely many sheets. If $K$ is a Galois extension, the Galois group $\mathrm{Gal}(K|k)$ is the group of deck transformations of this cover. Then subgroups $G \subseteq \mathrm{Gal}(K|k)$ correspond to intermediate fields

$$k \subseteq F \subseteq K$$

which correspond to what you might call ‘intermediate coverings’

$$\mathrm{Spec}(K) \to \mathrm{Spec}(F) \to \mathrm{Spec}(k)$$

And so on!

But there are some things missing from this wonderful analogy. First, we don’t yet have an analogue of the universal covering space of $\mathrm{Spec}(k)$, because this may not have finitely many sheets. Second, we don’t have an analogue of the fundamental group of $\mathrm{Spec}(k)$, since this may be an infinite group. And third, I have not described anything analogous to disconnected covering spaces.

All these deficiencies prevent us from stating a Galois theory analogue of the big result we had for covering spaces:

Theorem 9. Suppose $X$ is a compact connected manifold and $x \in X$. Then there is an equivalence between the category of compact covering spaces of $X$ and the category of finite sets equipped with an action of $\pi_1(X,x)$.

Grothendieck fixed this problem! And not just for fields — he handled all commutative rings and even more. But today I’m just doing fields.

The absolute Galois group

Let’s start by getting our hands on the Galois theory analogues of universal covering spaces and the fundamental group.

Any field $k$ has a separable closure $k^{\mathrm{sep}}$, which is a separable extension containing all finite separable extensions of $k$. It’s usually not a finite extension of $k$, but it’s a union of finite extensions. In fact it’s a union of Galois extensions!

The map

$$\mathrm{Spec}(k^{\mathrm{sep}}) \to \mathrm{Spec}(k)$$

acts like the universal covering space of $\mathrm{Spec}(k)$. $\mathrm{Spec}(k^{\mathrm{sep}})$ is too big to be a finite-sheeted covering space, but it maps down to any finite-sheeting connected covering space of $\mathrm{Spec}(k)$, since any Galois extension $K$ of $k$ is isomorphic to a subfield of $k^{\mathrm{sep}}$, giving us inclusions

$$k \subseteq K \subset k^{\mathrm{sep}}$$

and thus maps

$$\mathrm{Spec}(k^{\mathrm{sep}}) \to \mathrm{Spec}(K) \to \mathrm{Spec}(k)$$

Next, what about the fundamental group? In topology this is isomorphic to the group of deck transformations of the universal covering space. So the fundamental group of $\mathrm{Spec}(k)$ should be like $\mathrm{Gal}(k^{\mathrm{sep}}|k)$.

Beware: $k^{\mathrm{sep}}$ is not a Galois extension of $k$, since it’s not a finite extension. But we proceed with caution, and say the absolute Galois group of $k$ is the group of automorphisms of $k^{\mathrm{sep}}$ that fix $k$. It’s called $\mathrm{Gal}(k)$.

Since this is supposed to be the ‘mother of all Galois groups’, we would hope that any intermediate field

$$k \subseteq K \subseteq k^{\mathrm{sep}}$$

corresponds to some subgroup of $\mathrm{Gal}(k)$, and vice versa. Or something like that. But we are mainly interested in the case where $K$ is a finite separable extension of $k$, and it’s certainly not true that these correspond bijectively to subgroups of $G$. The group $\mathrm{Gal}(k)$ is too infinite, too wild and woolly, for that to be true.

So, what we do is put a topology on $\mathrm{Gal}(k)$ and show that the open subgroups of $\mathrm{Gal}(k)$ correspond to finite separable extensions of $k$.

That sounds a bit weird at first… we were trying to do algebra analogous to topology, but now topology has snuck into our algebra. But don’t worry: this topology is secretly just algebra. How do we put this topology on $\mathrm{Gal}(k)$? To make $\mathrm{Gal}(k)$ into a topological group we just need to give a base of open neighborhoods of the identity. And we’ll take these neighborhoods to be certain normal subgroups of $\mathrm{Gal}(k)$. Namely, for each intermediate field

$$k \subseteq K \subseteq k^{\mathrm{sep}}$$

that’s a Galois extension, we’ll take the subgroup of $\mathrm{Gal}(k)$ fixing every element of $K$!

With this choice, the thing we want happens!

Theorem 12. For any field $k$, the subset of $k^{\mathrm{sep}}$ fixed by some open subgroup $G \subseteq \mathrm{Gal}(k)$ is a finite separable extension of $k$, and this gives a one-to-one correspondence between

• intermediate fields $k \subseteq K \subseteq k^{\mathrm{sep}}$ that are finite separable extensions of $k$

and

• open subgroups of $\mathrm{Gal}(k)$.

Galois theory versus covering spaces

Theorem 12 is a nice analogue of the theorem we saw about connected covering spaces. Remember:

Theorem 10. Suppose $X$ is a connected compact manifold and $x \in X$. Then the category of connected compact covering spaces of $X$ is equivalent to the category of finite sets acted on transitively by $\pi_1(X,x)$.

How are they analogous? They look different! Theorem 12 gives one-to-one correspondence, while Theorem 10 gives an equivalence of categories. Theorem 12 talks about subgroups of some group, while Theorem 10 talks about transitive actions of some group. So there is a difference in style between these results, as well as a difference in subject matter.

Part of the point is that subgroups give transitive actions. If $H$ is a subgroup of a group $G$ then $G$ acts transitively on $G/H$ by left multiplication. And any transitive action of $G$ is isomorphic to one of this form. But it’s only isomorphic, not equal. So when we work with transitive group actions, we need to work with a category of them, not a set.

We could bridge this gap of styles and make Theorem 10 and Theorem 12 look more similar. But while we’re doing it, we might as well get rid of the connectedness assumption in Theorem 12. Doing the analogous thing in Theorem 10 gives us the fundamental theorem of Grothendieck’s Galois theory.

The fundamental theorem of Grothendieck’s Galois theory

Here it is:

Theorem 13 (The Fundamental Theorem of Grothendieck’s Galois Theory). The category of commutative separable algebras over a field $k$ is equivalent to the opposite of the category of finite sets equipped with a continuous action of the absolute Galois group $\mathrm{Gal}(k)$.

I hope you admire how it looks like the result I started with:

Theorem 9. Suppose $X$ is a connected compact manifold and $x \in X$. Then the the category of compact covering spaces of $X$ is equivalent to the category of finite sets equipped with an action of $\pi_1(X,x)$.

The opposite shows up in Theorem 13 because of the duality between commutative algebra and topology. The continuity shows up in Theorem 13 because we are putting a topology on the absolute Galois group to keep it under control.

I also hope you understand a bit about what Theorem 13 is claiming. Note that while a finite set $X$ has the discrete topology, it’s still not trivial to say an action

$$\mathrm{Gal}(k) \times X \to X$$

is continuous, since it has to be continuous in the first variable too, and $\mathrm{Gal}(k)$ has a nontrivial topology. Ultimately we’re saying that for some open neighborhood $U$ of the identity, $g \in U$ acts trivially on $X$. And by how we’ve defined the topology on $\mathrm{Gal}(k)$, we can assume $U$ is the subgroup of $\mathrm{Gal}(k)$ that fixes every element of some Galois extension of $k$.

This winds up meaning we can build $X$ from some Galois extension of $k$. And ultimately we do it using this:

Theorem 11. Any commutative separable algebra over a field $k$ is a finite product of finite separable extensions of $k$.

since we can find a Galois extension of $k$ that contains all these finite separable extensions.

I also hope you see what Theorem 13 says when $k$ is algebraically closed. Then its Galois group is trivial, and we get a result from last time:

Theorem 4$\prime$. Let $k$ be an algebraically closed field. Then the category of commutative separable algebras over $k$ is equivalent to the opposite of the category of finite sets.

Of course, you may still not deeply understand the Fundamental theorem of Grothendieck’s Galois theory. Maybe I don’t either. But I hope you see, at least roughly, that it strengthens the analogy between Galois theory and the theory of covering spaces… and in the case of algebraically closed fields it describes the category of finite sets using linear algebra! That’s a big deal.

There’s a lot left to explain, obviously. But what I really want to do next time is to say more about separable algebras. There are some huge questions I’ve left unanswered, like:

• Why are separable commutative algebras over a field $k$ precisely the ones that give covering spaces of $Spec(k)$?

• Why are separable commutative algebras over $k$ the same as finite products of finite separable extensions of $k$?

I do want to tackle these. But until then, try this:

Puzzle. Let $k$ be a field. Guess a recipe for getting a finite set $\Phi(A)$ on which $\mathrm{Gal}(k)$ acts continously from any commutative separable algebra $A$ over $k$. This recipe should be contravariant: a map of algebras $f \colon A \to A'$ should give a map $\Phi(f) \colon \Phi(A') \to \Phi(A).$ Can you guess a way to go back?

If you can do this, you’re well on your way to proving the fundamental theorem.

References

I think the most useful reference for today is this:

• Federico G. Lastaria, On separable algebras in Grothendieck Galois theory, Le Matematiche 51 No. 3 (1996).

We give an explicit proof of the fundamental theorem of Grothendieck Galois theory: the category of separable algebras over a field $k$ is anti-equivalent to the category of continuous actions on finite sets of the profinite fundamental group of $k$.

That group is the absolute Galois group of $k$. For the topology on this group, and basic facts about how that topology works, I also recommend this:

• Juergen Neukirch, Algebraic Number Theory: Chapter IV.1, Infinite Galois Theory, Springer, Berlin, 2013.

Both these references have the advantage of being quite down-to-earth.