June 26, 2025
Counting with Categories (Part 3)
Posted by John Baez
Here’s my third and final set of lecture notes for a 4-hour minicourse at the Summer School on Algebra at the Zografou campus of the National Technical University of Athens.
Part 1 is here, and Part 2 is here.
Counting with Categories (Part 2)
Posted by John Baez
Here’s my second set of lecture notes for a 4-hour minicourse at the Summer School on Algebra at the Zografou campus of the National Technical University of Athens.
Part 1 is here, and Part 3 is here.
June 22, 2025
Counting with Categories (Part 1)
Posted by John Baez
These are some lecture notes for a 4-hour minicourse I’m teaching at the Summer School on Algebra at the Zografou campus of the National Technical University of Athens. To save time, I am omitting the pictures I’ll draw on the whiteboard, along with various jokes and profoundly insightful remarks. This is just the structure of the talk, with all the notation and calculations.
Long-time readers of the -Category Café may find little new in this post. I’ve been meaning to write a sprawling book on combinatorics using categories, but here I’m trying to explain the use of species and illustrate them with a nontrivial example in less than 1.5 hours. That leaves three hours to go deeper.
Part 2 is here, and Part 3 is here.
June 1, 2025
Tannaka Reconstruction and the Monoid of Matrices
Posted by John Baez
You can classify representations of simple Lie groups using Dynkin diagrams, but you can also classify representations of ‘classical’ Lie groups using Young diagrams. Hermann Weyl wrote a whole book on this, The Classical Groups.
This approach is often treated as a bit outdated, since it doesn’t apply to all the simple Lie groups: it leaves out the so-called ‘exceptional’ groups. But what makes a group ‘classical’?
There’s no precise definition, but a classical group always has an obvious representation, you can get other representations by doing obvious things to this obvious one, and it turns out you can get all the representations this way.
For a long time I’ve been hoping to bring these ideas up to date using category theory. I had a bunch of conjectures, but I wasn’t able to prove any of them. Now Todd Trimble and I have made progress:
- John Baez and Todd Trimble, Tannaka reconstruction and the monoid of matrices.
We tackle something even more classical than the classical groups: the monoid of matrices, with matrix multiplication as its monoid operation.
April 16, 2025
Position in Stellenbosch
Posted by John Baez
guest post by Bruce Bartlett
Stellenbosch University is hiring!
April 15, 2025
Categorical Linguistics in Quanta
Posted by Tom Leinster
Quanta magazine has just published a feature on Tai-Danae Bradley and her work, entitled
Where Does Meaning Live in a Sentence? Math Might Tell Us.
The mathematician Tai-Danae Bradley is using category theory to try to understand both human and AI-generated language.
It’s a nicely set up Q&A, with questions like “What’s something category theory lets you see that you can’t otherwise?” and “How do you use category theory to understand language?”
Particularly interesting for me is the part towards the end where Bradley describes her work with Juan Pablo Vigneaux on magnitude of enriched categories of texts.
April 7, 2025
Quantum Ellipsoids
Posted by John Baez
With the stock market crash and the big protests across the US, I’m finally feeling a trace of optimism that Trump’s stranglehold on the nation will weaken. Just a trace.
I still need to self-medicate to keep from sinking into depression — where ‘self-medicate’, in my case, means studying fun math and physics I don’t need to know. I’ve been learning about the interactions between number theory and group theory. But I haven’t been doing enough physics! I’m better at that, and it’s more visceral: more of a bodily experience, imagining things wiggling around.
So, I’ve been belatedly trying to lessen my terrible ignorance of nuclear physics. Nuclear physics is a fascinating application of quantum theory, but it’s less practical than chemistry and less sexy than particle physics, so I somehow skipped over it.
I’m finding it worth looking at! Right away it’s getting me to think about quantum ellipsoids.
March 26, 2025
The McGee Group
Posted by John Baez
This is a bit of a shaggy dog story, but I think it’s fun. There’s also a moral about the nature of mathematical research.
Once I was interested in the McGee graph, nicely animated here by Mamouka Jibladze:
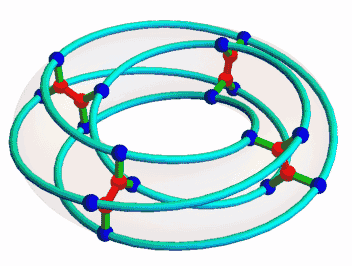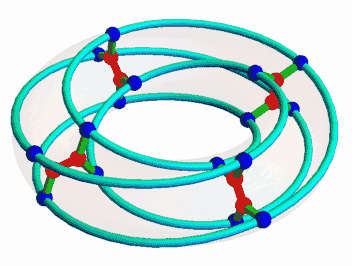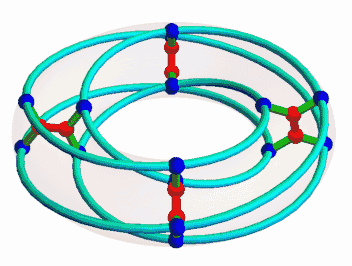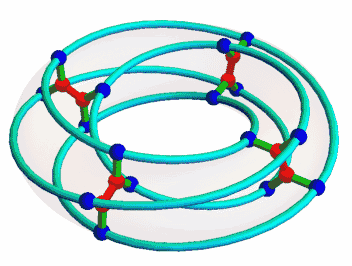
This is the unique (3,7)-cage, meaning a graph such that each vertex has 3 neighbors and the shortest cycle has length 7. Since it has a very symmetrical appearance, I hoped it would be connected to some interesting algebraic structures. But which?
March 20, 2025
Visual Insights (Part 2)
Posted by John Baez
From August 2013 to January 2017 I ran a blog called Visual Insight, which was a place to share striking images that help explain topics in mathematics. Here’s the video of a talk I gave last week about some of those images:
It was fun showing people the great images created by Refurio Anachro, Greg Egan, Roice Nelson, Gerard Westendorp and many other folks. For more info on the images I talked about, read on….
March 12, 2025
Category Theory 2025
Posted by Tom Leinster
Guest post by John Bourke.
The next International Category Theory Conference CT2025 will take place at Masaryk University (Brno, Czech Republic) from Sunday, July 13 and will end on Saturday, July 19, 2025.
Brno is a beautiful city surrounded by nature with a long tradition in category theory. If you are interested in attending, please read on!
Important dates
- April 2: talk submission
- April 18: early registration deadline
- May 7: notification of speakers
- May 23: registration deadline
- July 13-19: conference
In addition to 25 minute contributed talks, there will be speed talks replacing poster sessions, and we hope to accommodate as many talks as possible.
The invited speakers are:
- Clark Barwick (University of Edinburgh)
- Maria Manuel Clementino (University of Coimbra)
- Simon Henry (University of Ottawa)
- Jean-Simon Lemay (Macquarie University)
- Wendy Lowen (University of Antwerp)
- Maru Sarazola (University of Minnesota)
March 7, 2025
Visual Insights (Part 1)
Posted by John Baez
I’m giving a talk next Friday, March 14th, at 9 am Pacific Daylight time here in California. You’re all invited!
(Note that Daylight Savings Time starts March 9th, so do your calculations carefully if you do them before then.)
Title: Visual Insights
Abstract: For several years I ran a blog called Visual Insight, which was a place to share striking images that help explain topics in mathematics. In this talk I’d like to show you some of those images and explain some of the mathematics they illustrate.
Zoom link: https://virginia.zoom.us/j/97786599157?pwd=jr0dvbolVZ6zrHZhjOSeE2aFvbl6Ix.1
Recording: This talk will be recorded, and eventually a video will appear here: https://www.youtube.com/@IllustratingMathSeminar
March 4, 2025
How Good are Permutation Represesentations?
Posted by John Baez
Any action of a finite group on a finite set gives a linear representation of on the vector space with basis . This is called a ‘permutation representation’. And this raises a natural question: how many representations of finite groups are permutation representations?
Most representations are not permutation representations, since every permutation representation has a vector fixed by all elements of , namely the vector that’s the sum of all elements of . In other words, every permutation representation has a 1-dimensional trivial rep sitting inside it.
But what if we could ‘subtract off’ this trivial representation?
There are different levels of subtlety with which we can do this. For example, we can decategorify, and let:
the Burnside ring of be the ring of formal differences of isomorphism classes of actions of on finite sets;
the representation ring of be the ring of formal differences of isomorphism classes of finite-dimensional representations of .
In either of these rings, we can subtract.
There’s an obvious map , since any action of on a finite set gives a permutation representation of on the vector space with basis .
So I asked on MathOverflow: is typically surjective, or typically not surjective?
February 26, 2025
Potential Functions and the Magnitude of Functors 2
Posted by Tom Leinster
Despite the “2” in the title, you can follow this post without having read part 1. The whole point is to sneak up on the metricky, analysisy stuff about potential functions from a categorical angle, by considering constructions that are categorically reasonable in their own right. Let’s go!
February 23, 2025
Potential Functions and the Magnitude of Functors 1
Posted by Tom Leinster
Next: Part 2
In the beginning, there were hardly any spaces whose magnitude we knew. Line segments were about the best we could do. Then Mark Meckes introduced the technique of potential functions for calculating magnitude, which was shown to be very powerful. For instance, Juan Antonio Barceló and Tony Carbery used it to compute the magnitude of odd-dimensional Euclidean balls, which turn out to be rational functions of the radius. Using potential functions allows you to tap into the vast repository of knowledge of PDEs.
In this post and the next, I’ll explain this technique from a categorical viewpoint, saying almost nothing about the analytic details. This is category theory as an organizational tool, used to help us understand how the various ideas fit together. Specifically, I’ll explain potential functions in terms of the magnitude of functors, which I wrote about here a few weeks ago.
February 17, 2025
Category Theorists in AI
Posted by John Baez
Applied category theorists are flocking to AI, because that’s where the money is. I avoid working on it, both because I have an instinctive dislike of ‘hot topics’, and because at present AI is mainly being used to make rich and powerful people richer and more powerful.
However, I like to pay some attention to how category theorists are getting jobs connected to AI, and what they’re doing. Many of these people are my friends, so I wonder what they will do for AI, and the world at large — and what working on AI will do to them.
Let me list a bit of what’s going on. I’ll start with a cautionary tale, and then turn to the most important program linking AI and category theory today.
 Posts with this logo use
Posts with this logo use 














