Frobenius Algebroids with Invertible Products
Posted by Urs Schreiber
Sometimes, banalities fool us into ignoring important structure. That happens when the banality is the degenerate case of something that is in general more interesting.
One banality is this.
An associative monoidoid (I mean any enriched category, please see the comments below)
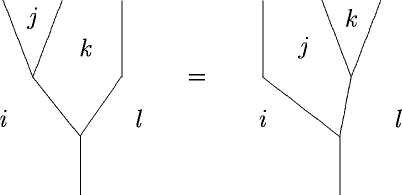
with invertible product (this invertibility is the degeneracy)
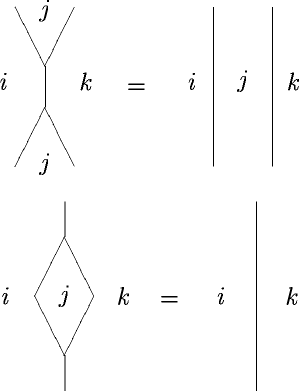
is naturally a Frobenius monoidoid
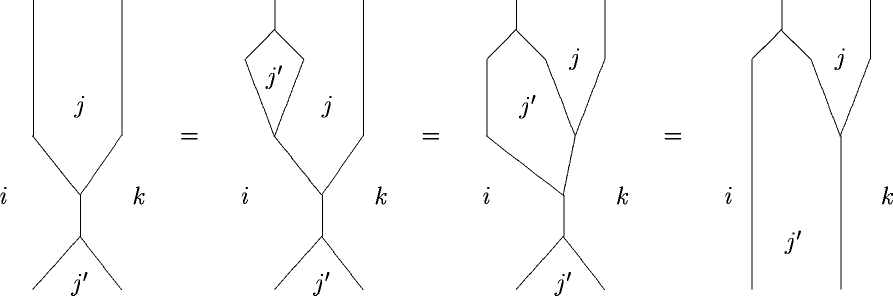
only that you would tend to ignore this fact. It’s like ordering Pizza Tonno without Tuna.
But notice this:
when we compute gerbe holonomy in local data, we are inclined to choose a dual triangulation of our surface and decorate it with the transition data – which amounts to decorating it in a monoidoid with invertible product.
On the other hand, when we compute amplitudes in 2-dimensional field theory using state sum models, we are inclined to choose a dual triangulation of our surface and decorate it in a Frobenius algebroid.
I want to invite everybody to think of these two procedures as two versions of the same underlying principle. I used to call this principle locally trivialized 2-transport. But apparently I should start referring to it in terms of 2-anafunctors.
So when I give two talks in Toronto # – even though I have only one point to make – it is because there are two aspects to this one point: 2-anafunctors come in two flavors: with pseudo transitions or with lax transitions.
I try to tell parts of this story here. The plot follows this table:


Re: Frobenius Algebroids with invertible Products
What the heck is a “monoidoid”? It’s not good to use such quirky terminology without defining it.
An “algebroid” is a category enriched over Vect; this terminology is justified by the fact that a one-object algebroid is an algebra.
A “ringoid” is a category enriched over AbGp; this terminology is justified by the fact that a one-object ringoid is a ring.
So, I’d have to guess that:
A “monoidoid” is a category enriched over Set; this terminology is justified by the fact that a one-object monoidoid is a monoid.
But, a category enriched over Set is just a category!
So, I’m forced to guess that “monoidoid” is your quirky new terminology for “category”.
But, I can’t believe you’d be that perverse.