QFT of Charged n-Particle: The Canonical 1-Particle
Posted by Urs Schreiber
A category of histories for the 1-particle, whose Leinster measure reproduces (a discretized approximation of the Euclidean version of) the path integral measure for the charged 1-particle on the real line.
I present something which should be at least part of the solution to the exercise that we started to think about in Canonical Measures on Configuration Spaces: the goal is to set up the categories encoding target space and history space of the charged 1-particle in such a way that the canonical Leinster measure on the category of histories provides the right measure for the path integral that yields the quantum dynamics.
General Preliminaries: the Construction put in Perspective.
The quantum theory of the charged -particle is a setup which (see also John Baez’ description of this idea)
a) reads in a diagram of -categories of the form
and supposed to encode
- the shape of an -particle ()
- the background spacetime it propagates in )
- the background gauge field it is charged under
and
b) spits out the corresponding quantum theory.
Remarkably, given the diagram (1), everything about this procedure is apparently rather canonical, in that it involves only the natural and obvious pull-push diagrams that can be obtained from (1).
But what may be natural for nature might not always be obvious to us (as nicely pointed out by David Corfield and John Baez here and here).
So let’s be careful. In the present context, a mighty subtlety resides in the way the background gauge field is encoded in its parallel transport -functor
Concentrate on . Usually, we consider 1-particles coupled to vector bundles with connection and hence consider vector transport associated to some principal transport for gauge group (structure group) .
This looks all fine – but may be too simple minded:
by the reasoning reviewed in -Transport and Higher Schreier Theory, the right principal transport is not a functor with values in the group, but a pseudofunctor with values in the group’s 2-group of inner automorphisms
For principal 1-transport the difference is essentially invisible, as described in -Curvature.
But for the associated 1-vector transport this makes a big difference. The naïve representation which we use to associate vector transport to principal transport, will have to to be replaced by some suitable domain of “phases” which now is a 2-category itself.
The important consequence is that this implies that the space of sections of the background field is then a (1-)category, instead of a mere set.
In a context where everything is done using pulling and pushing, this difference is huge: for objects in a category, there are canonical notions of these procedures, while for elements of sets one has to introduce extra structure by hand (measures, in particular), in order to perform analogous constructions.
To see this more clearly, consider the special case where the background gauge field is trivial, such that is the tensor unit in the category of all these background fields.
Then a section, , of this bundle is an assignment
of 2-cells in to paths in target space.
Here the assignment on objects is the usual assignment of values to points, that you’d expect from a section of a bundle. But since we are being sophisticated and non-naïve, the section now also assigns morphisms between these values to paths in target space.
So we find that a section is not just a function (locally) on target space, but in fact a functor.
(Notice that it is really a contravariant functor. This is not important for the general point of view currently described, but becomes crucial as soon as we perform concrete computations with these sections.)
A Canonical Measure for Quantization: the Leinster Measure
These functors, in turn, have morphisms between them. This implies that there is, in general, a natural way to push such sections forward to a point, for instance. At the decategorified level, such a procedure amounts essentially to integrating these sections. In the more familiar approach, where we do not realize our background field parallel transport by a pseudofunctor, but just by a 1-functor, sections are mere elements of sets, and integrating them requires specifying (“by hand”) a measure.
Interestingly, once we allow sections to be functors themselves, there is a god-given structure that plays the role of this integration measure, otherwise chosen by hand. This is the Leinster Measure on the corresponding domain category.
The observation that the Leinster measure seems to induce a canonical measure for the quantization procedure was discussed in Canonical Measures on Configuration Spaces.
There, the general concept was described, and some attempts at relating the structure of the target space category with the expected measure needed for the quantization of the relativistic particle were listed. Making this example more concrete had remained an unfinished exercise:
Exercise. Find (1) such that the entirely canonical quantization procedure applied to it, in particular using the Leinster measure as described above, reproduces (a discrete approximation to) the ordinary textbook quantum theory of the charged 1-particle.
Solution to the Exercise: the Non-Relativistic Charged 1-Particle
Here I want to spell out what seems to be a solution to this exercise which applies to the non-relativistic particle.
I shall consider the particle propagating on a 1-dimensional target space, for simplicity and clarity. Generalizations should, however, be rather obvious.
Caveat: the Nature of our Quantum Phases
There are two main points where the solution that I present below eventually needs to be filled in with more details. So really it is a solution only modulo these pending issues, which I shall simply trust can be dealt with. Hopefully I am right.
While in the naïve setup it is clear that our charged particle should couple to a parallel transport with values in , it is not fully clear to me at the moment what exactly best replaces this choice as we do the non-naive version.
One option I considered, inpired by Jeffrey Morton’s work on categorified quantum theory, is passing from the 1-category to the 2-category by replacing, throughout, complex numbers by sets with maps to the complex numbers. I made some remarks on how to proceed in this case here.
After thinking about this for a while, I began to wonder if something more linear might be closer to the truth. Such as , the 2-category of module categories for -graded (assuming we can deal with that) vector spaces.
At least up to the detail of the grading, and always assuming that the -valued functors that we shall be dealing with can be taken to satisfy the assumptions that go into Tom Leinster’s theorem, both of these options seem to make the following construction work: direct sums of sets as well as of vector spaces acts as ordinary sum on the isomorphism classes (cardinality and dimension, respectively).
But I am convinced that nature has a completely natural answer concerning the right choice of the 2-category of quantum phases, and I am not convinced that I am at the point of seeing this yet.
Therefore I’ll leave the deatails of this issue for later, and tentatively propose either of the above two choices as a working definition that helps us to proceed with what shall be the main issue here: the determination of a category of histories with the right Leinster measure on it to reproduce the quantization measure for the charged 1-particle.
The Target Space Category
After all these preliminaries, here finally the construction itself.
As a model for 1-dimensional space, take the category freely generated from the directed graph of the form
Parameter space for the 1-particle is, as usual, just the discrete category on a single object Configuration space is simply the space of all maps of parameter space into target space, i.e. For the particle, configuration space and target space coincide. (Notice that I am not, at this point, using the extended configuration space. Compare the discussion here.).
What is the space of histories, i.e. of paths of the 1-particle in target space ?
The worldvolume of the 1-particle is a Riemannian 1-manifold, which I shall model by the category freely generated as We think of this as a cobordism between two copies of our parameter space, which form the two boundaries of the worldline.
The category of histories is a subcategory of that of all maps of this into target space I discuss below how to determine this subcategory.
Pull-Push of States
By precomposing with the injection maps and , we may restrict any history to the configuration at its beginning and at its end, respectively:
Propagation of the 1-particle over a time interval is the operation on states obtained by pull-pushing through this correspondence.
As recalled in (2), a state, here, is a transformation between transport functors on target space, which model the background field that the particle couples to. While it is immediate what the pullback of a functor along would be, the pullback of a transformation of functors through this correspondence needs a little more care:
The fact that a history interpolates between two configurations is very concretly realized in the existence of a transformation
between the projection onto its boundary components.
A moment of reflection shows that the pullback of states that we need is the operation of pasting this 2-morphism to that of a state to obtain

The precomposition with the 1-morphism accomplishes the naive pullback from configurations to histories. The composition with the 2-morphism then takes care of the parallel transport of all these sections to the other end of our cobordism.
I have described this in more detail in QFT of Charged n-Particle: Dynamics.
Evolution over Small Time Intervals
Now, the standard propagator for the (Euclidean) particle on the line is where is the covariant Laplace operator on target space, coming from the vector bundle with connection that is encoded in our parallel transport functor .
We want to find the category such that pulling sections back to along the above lines, and then pushing forward from the space of histories to the space of configurations along reproduces this propagator (for more on the relation of this propagator to the corresponding path integral see John Baez’s lecture “Quantization and Cohomology ” week 14 and week 15).
Since we have approximated target space by a lattice, we need the corresponding lattice version of the covariant Laplace operator, which reads It is helpful to first consider propagation over “infinitesimal” time intervals, for which we approximate Hence we need to find such that the pull-push through (3) produces
I claim that this is the case if we let be that full subcategory, which contains all functors that send the unit length worldline at most to an edge of the target space category (instead of to a morphism obtained as an arbitrary concatenation of edges), and whose morphisms only contract, never expand their image.
More precisely, is the subcategory of all “maps” (functors) from the 1-unit worldvolume into target space definined by the two restrictions
a) objects are only those functors that are at the same time morphisms of the underlying graphs, i.e. which map the single edge either to an identity in or to a single edge in .
b) morphisms are all natural transformations between these, except for those which would go from an identity image to a non-identity image .
To see that pull-push propagation through does indeed reproduce propagation by the lattice Laplace operator, notice that the subcategory of all paths ending at simply looks like
Pulling a state back to this by means of (3) produces the transformation given by the assignment
This assignment of 2-morphisms to 1-morphisms is a contravariant functor on . Therefore the colimit of this is controlled by the Leinster measure on the oppositecategory, , of : The Leinster measure on this simple category is
This means that, assuming that our state is such that the morphisms and are suitably monic and denoting by the isomorphism class in our choice of (compare the discussion above) then the colimit of the state pulled back to , according to (3), is This is our path integral! Over paths of “very small length”. By (4) we can rewrite this as
Evolution over two Small Time Intervals
The category of 2-step histories should be the composite span of with itself, i.e. the pullback
I think looks, explicitly, as follows.
Let now be the worldline of length two units of time and consider The subcategory of that these histories (paths) are allowed to map into is

The category of 2-step histories ending at looks like
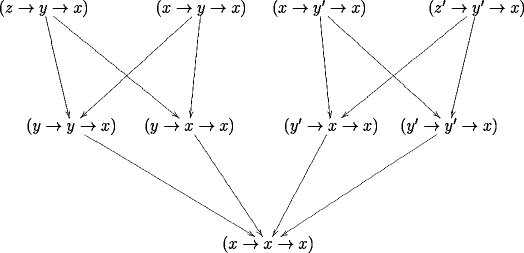
The Leinster measure on the opposite of the above category (remember that our states are contravariant functors) is
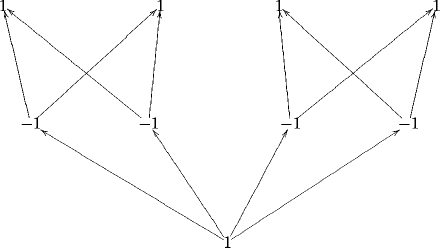
(Notice that all parallel morphisms in , hence also in its opposite, are equal, in the present context).
But this means that the path integral now yields This one checks, by applying (4) twice, is the same as if we again approximate the exponential by its leading contribution.

Re: QFT of Charged n-Particle: The Canonical 1-Particle
I’ve already gushed about how awesome I think all this is, so I won’t repeat myself other than to ask why you insist on calling this an “approximation” to the continuum. Perhaps the continuum is the approximation ;)