Penrose on Angular Momentum: An Approach to Combinatorial Space-Time
Posted by John Baez
Georg Beyerle has created an electronic version of a classic paper on spin networks that was previously available only in an out-of-print book:
- Roger Penrose, Angular momentum: an approach to combinatorial space-time.
Roger Penrose has given me permission to put it on my website. Take a copy! If you spot typos, please let me know.
Here’s what a piece of a spin network looks like:
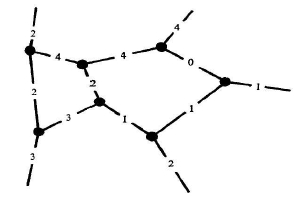
Can we build space, or spacetime, out of something as simple as this? That’s the question Penrose tackles in his paper.

Re: Penrose on Angular Momentum: An Approach to Combinatorial Space-Time
This is one of my all time favorite papers. Thanks for making it available electronically!