Charges and Twisted n-Bundles, I
Posted by Urs Schreiber
I want to talk about
twisted -bundles with connection over -dimensional base space
coupled to
(electrically) charged -particles (()-branes);
how they are
sections with covariant derivatives of -bundles with connection
which can be interpreted as
obstructions to lifts through extensions of -groups
or equivalently
magnetic charges
of
magnetically charged ()-particles (()-branes).
A crucial new ingredient compared to my former (I,II) discussion of sections of -bundles is the method from groupoidification: think of an -representation of an -group not as an -functor, but in terms of the corresponding action -groupoid, as described more recently in -associated bundles and sections.
Much of what I say is, in the language of generalized differential cohomology, in the great
D. S. Freed
Dirac Charge Quantization and Generalized Differential Cohomology
(arXiv)
only that what I describe in the language of -parallel transport/-connections (pdf, arXiv, blog, brief slides, detailed slides) is supposed to be a nonabelian generalization of the purely abelian treatment which allows to not just say things like
The Green-Schwarz mechanism says that the Kalb-Ramond 2-bundle coupling to the electric string is twisted by magnetic 5-brane charge.
(discussion around equation (3.5) in Freed’s article)
But also things like
The Green-Schwarz mechanism says that over the 10-dimensional boundary of 11-dimensional supergravity base space the supergravity Chern-Simons 3-bundle obstructing the lift of an -bundle to a -2-bundle trivializes by admitting a global 2-section: the twisted Kalb-Ramond 2-bundle.
(previewed in section 3 of -connections)
where the underlying -bundle as well as its String-2-bundle lift with connections represent nonabelian differential cohomology.
LaTeXified notes on what I will talk about are beginning to evolve as
Sections and covariant derivatives of -algebra connections
(pdf, blog, Bruce Bartlett’s recollection)
and
Twisted -connections
(pdf).
The quick way to see it.
If you have absorbed section 8 then everything more or less follows from the following simple observation (if not jump to the next paragraph right now!):
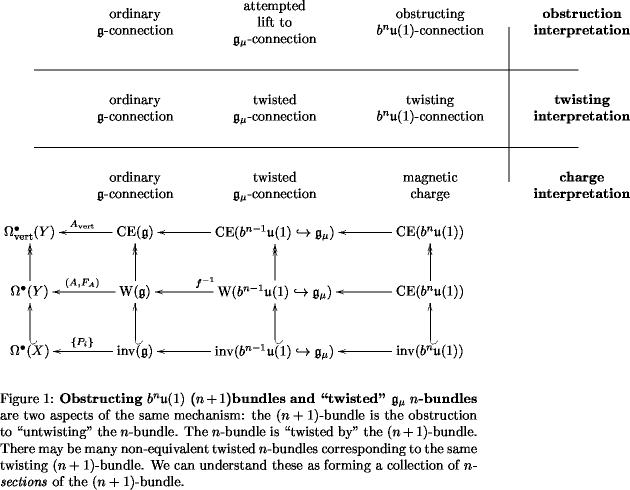
The more expository approach
It will have to be seen how far I can get right now. But it is fun to start with this
Simple reconsiderartion of ordinary electromagnetism aka abelian 1-gauge theory,
as found, with the emphasis we need here, in section 2 of Freed’s article as well as in most every other review of D-brane physics (aka higher generalized electromagnetism aka abelian -gauge theory) like, er, let’s see… p. 111 here:
Clifford Johnson
D-Brane Primer
(arXiv, book homepage).
So the phenomenon of interest here is a generalization to
- a) higher dimensions (meaning higher dimensions of target space);
- b) higher categorical dimensions (meaning higher dimensions of parameter space);
- c) nonabelian structures
of the following high-school facts (well, maybe most highschool don’t teach them this way, which is a pity, because it could easily be taught this way)
So an electromagnetic field on a space is a closed 2-form
If there are electrons zipping around on , then the fact that they are charged under the electromagnetic field means that whenever they trace out closed curves in , we can consistently assign a phase
to that curve, an element in , with the property that whenever
is the boundary of a disk , we have
This implies that is actually integral, meaning that its integral over any closed surface in is an integer:
From this one concludes that is in fact the curvature of a line bundle with connection on .
[An important special case is and the Hopf bundle . As Jim Stasheff emphasises, it is the most remarkable fact about the history of science that P. A. M. Dirac found this line bundle from the physics perspective descibed here in the very same year, 1931, that Hopf described his line bundle – and that this was fully appreciated not until decades later (Jim says by Greub and Petry, 1975).]
The electrons zipping around on produce themselves an electromagnetic field. It turns out that this affects the electromagnetic line bundle we are talking about by the constraint that
where
is the Hodge star operator induced from a choice of (pseudo-)Riemannian metric on ; and
is a 3-form which is Poincaré dual to the curves that our electrons trace out.
Electrons are electrically charged. What happens when magnetically charged particles also zip around on (like the two ends of an ideal current-carrying coil (not to mention just yet the two ends of a string))?
It turns out that in that case there is another 3-form, , such that now
is replaced by
Now, that should be a little shocking. A moment ago we had luckily identified two major concepts in physics and math – electromagnetic fields and line bundles with connection. That identification breaks down as be allow nonvanishing ! The curvature 2-form of a line bundle with connection has no chance but to be closed.
So what’s going on? What is the mathematical structure which is to like ordinary line bundles with connection are to ?
The answer is: twisted bundles.
And strikingly: twisted bundles are really 2-bundles. There is 2-categorical physics around already in 1931, secretly.
And there is an easy way to understand this heuristically: I just mentioned that we get magnetic charges from ideal (infinitely thin) current carrying coils on – which look like strings. 2-Particles. As they move, they trace out a 2-dimensional volume, not just a curve. So they naturally couple to a 2-bundle!
Which 2-bundle could that possibly be? Easy: the line 2-bundle whose curvature 3-form is just the current 3-form
Which incidentally implies that
a) - the current 3-form has to be integral, too
which incidentally means that “charge is quantized”: it comes in integr multiples of a fixed unit;
b) since it satisfies , it must come from a 2-bundle/1-gerbe whose class in is “pure torsion” (vanishes when multiplied with some finite integer).
The math language for electromagnetic fields in the presence of magnetic charge is hence
The magnetic charge is a line 2-bundle which is trivialized by the electromagnetic field, which is a “twisted 1-bundle” or “gerbe module”.
I’ll say more about what this really means later. For the moment, I just want to collect the items in a dictionary relating math and physics here.
Suppose is -dimensional. And suppose we are talking about electrically charged -particles (known as ()-branes). Then
An
electrically charged -particle
on , known as a
electrically charged -brane
couples to an
electromagnetic -bundle with connection
on , with
curvature -form
also known as a
-gerbe with connection and curving
which is “twisted” by a
magnetic charge -bundle
with curvature -form
known as the magnetic current.
And we get the analogous story with electric and magnetic exchanged everywhere. In fact, it is a coincidence that in the four dimensions which we are familiar with, electrically charged particles correspond also to magnetically charged particles. In other dimensions that fails.
For dimensional , we have that:
if an electrically charged -particle couples to a field with
curvature -form
then the Hodge dual form
may happen to be the curvature -form of
a -bundle with connection which couples to
-particles.
These latter we then call “magnetically charged”.

Re: Charges and Twisted n-Bundles, I
Maybe this is why there are no other comments on this blog entry yet: the comprehensible stuff starts only after a page of terrifyingly technical references, an offhand remark about how a supergravity Chern-Simons 3-bundle can obstruct the lift of an -bundle to a String -2-bundle, and a huge commutative diagram full of undefined symbols.
But it’s not really that hard once Urs gets going!
So, I urge readers to give this article another try, skipping everything until you see this section header:
The more expository approach
I also urge Urs to rewrite this entry, simply by removing most of the scary stuff at the top.