This Week’s Finds in Mathematical Physics (Week 273)
Posted by John Baez
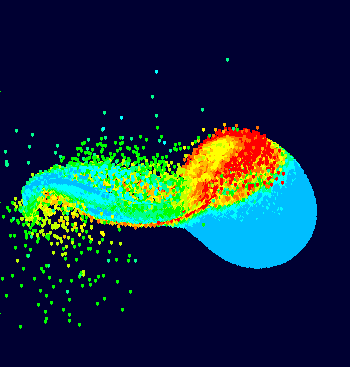
In week273 of This Week’s Finds, read more about the geysers on Enceladus. Hear the story of the Earth, with an emphasis on mineral evolution — from chondrites to the Big Splat, the Late Heavy Bombardment, the Great Oxidation Event, Snowball Earth… to now.
Then, learn about Pontryagin duality!
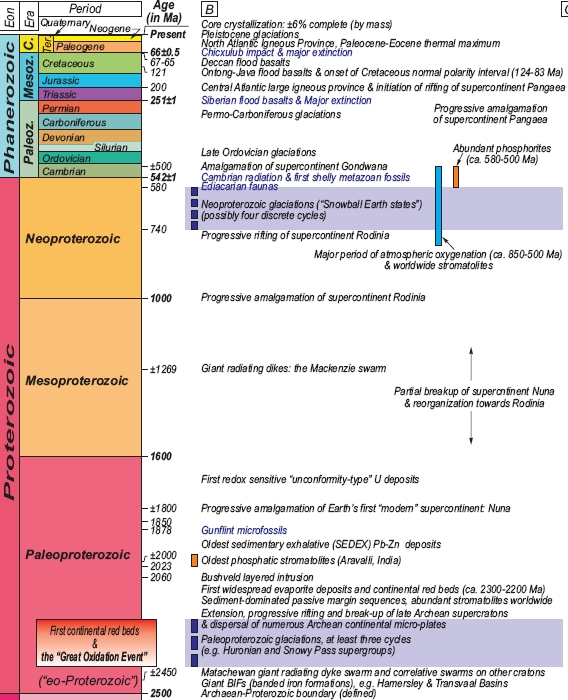
Here’s a cool chart from this paper:
- Robert M. Hazen, Dominic Papineau, Wouter Bleeker, Robert T. Downs, John M. Ferry, Timothy J. McCoy, Dmitri A. Sverjensky and Henxiong Yang, Mineral evolution, American Mineralogist 91 (2008), 1693-1720.





Re: This Week’s Finds in Mathematical Physics (Week 273)
Just before the big splat “The ‘first atmosphere’ was mainly hydrogen and helium”, but was there a first ocean? I ask this question because I am wondering whether comets that we see nowadays could be these very energetic tiny particles in Mackenzie’s animation that correspond to the impact point of Theia with Earth.