Understanding the Homotopy Coherent Nerve
Posted by Mike Shulman
(guest post by Emily Riehl)
Simplicial categories, more properly called simplicially enriched categories, provide a model for -categories which is related to quasi-categories by means of an adjunction sSet sSet-Cat. This adjunction induces a Quillen equivalence between André Joyal’s model structure on simplicial sets and Julie Bergner’s model structure on simplicial categories. Consequently, this adjunction serves as a primary means of translating between the two worlds, figuring prominently, for example, in the straightening construction, which is the -analog of the classical Grothendieck construction of a contravariant Cat-valued pseudofunctor from a categorical fibration.
The main disadvantage to this perspective is that the functor , although defined explicitly as a pointwise left Kan extension, is not easily understood – or rather, was not easily understood until a recent paper by Dugger and Spivak. Their “necklace characterization,” detailed below, makes it easy to compute the simplicial categories associated to simplicial sets as well as prove a number of results, at least one of which is rather surprising.
We’ll begin by reviewing the definition of the homotopy coherent nerve , which we present, following Dugger and Spivak, by means of a comonad resolution, a perspective we find more intuitive than the usual one. We’ll then turn our attention to the left adjoint and explain the details of the necklace characterization. At the conclusion, we’ll give a number of applications, most of which can be found in more detail here.
The homotopy coherent nerve
By familiar abstract nonsense, the adjunction is uniquely determined by a functor ΔsSet-Cat, which sends each object of Δ Cat to a simplicial category . The simplicial category is a cofibrant replacement of the trivial simplicial category structure on the poset category and has the same objects 0, 1, , . Its hom-spaces are typically defined to be nerves of certain poset categories, but we prefer an alternate description.
There is a free-forgetful adjunction rGrphCat between small categories and reflexive graphs, which are directed graphs equipped with an identity edge at each vertex. This adjunction induces a comonad on Cat and the resulting comonad resolution defines a simplicial object in Cat
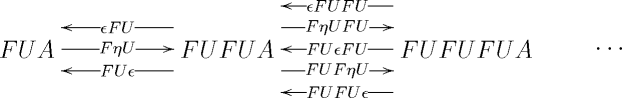
for any (ordinary) small category . A simplicial object in Cat gives rise to a simplicial category if and only if all of the functors involved are identities on objects, which is the case here. The -simplices of the hom-object from and are the morphisms from hom-set .
Unraveling the definition, the 0-simplices of this simplicial category are strings of composable non-identity morphisms in ; the 1-simplices are strings of morphisms where every morphism appears in exactly one set of parentheses; the 2-simplices are strings where every morphism appears in exactly two sets of parentheses; and so forth. The face maps remove the parentheses that are contained in exactly others; composes the morphisms inside the innermost parentheses. The degeneracy maps double up the parentheses that are contained in exactly others; inserts parentheses around each individual morphism.
When we let be the poset category , the simplicial category arising from this comonad resolution is , as usually defined. For example, let’s compute the hom-object for the simplicial category associated to the poset category with objects 0, 1, 2, 3 and morphisms as shown
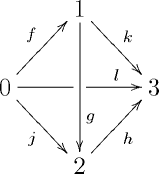
Examining the morphisms of from 0 to 3 we see there are four 0-simplices: , , , and . Similarly, examining reveals nine 1-simplices - , , , , , , , , and - the last four of which are degenerate. Finally, examining reveals two non-degenerate 2-simplices and with boundary as indicated
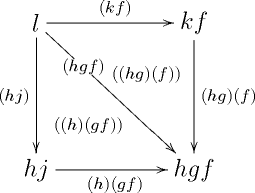
together with 14 degenerate ones. There are no non-degenerate higher simplices. Hence, .
In general, the hom-object is empty if , a point if , and the cube when .
The homotopy coherent nerve of a simplicial category is the simplicial set with sSet-Cat. So, for example, the data of a 3-simplex in the homotopy coherent nerve of consists of four objects , , , of ; 6 vertices , , , , , and ; 1-simplices , , , , (where the new vertices are defined using the horizontal composition of ); and two 2-simplices in whose boundary edges are depicted below.
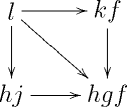
Understanding the hom-spaces of
Now let’s turn our attention to the left adjoint . Let be a simplicial set. By definition
Morally,
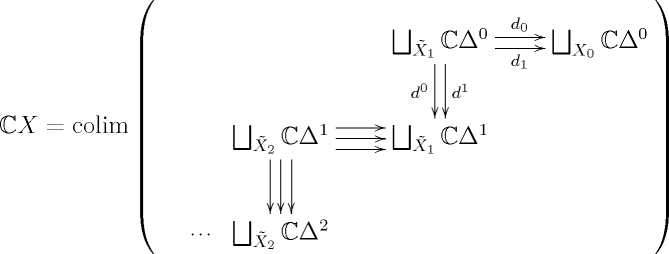
where denotes the non-degenerate -simplices of .
The objects of are the vertices of . The simplicial categories and are the free simplicial categories on the poset categories and respectively, and the free simplicial category functor is a left adjoint and so commutes with colimits. Hence, if is 1-skeletal so that for all , then is the free simplicial category on the graph with vertex set and edge set . Concretely, this means that the hom-spaces are all discrete simplicial sets containing a vertex for each path of edges from to in .
In general, for each 2-simplex of with 2nd face , 0th face , and 1st face , there exists a 1-simplex from the vertex to the vertex in . Furthermore, for each vertex in some hom-space representing a sequence of paths containing , there is a 1-simplex connecting it to the vertex representing the same sequence, except with in place of .
However, the 2-skeleton of does not determine the 1-skeleta of the hom-spaces. For example, for each 3-simplex of as depicted by (1), there is an edge from to in . In general, there is an edge between the vertices represented by paths and of edges from to in if and only if each edge in the first path that does not appear in the second is replaced by a sequence of -edges that appear as the spine of some -simplex of with as its diagonal. Here, the spine of an -simplex is the sequence of edges between the adjacent vertices, using the usual ordering of the vertices, and the diagonal is the edge from the initial vertex to the final one.
In this way, each edge of corresponds to a necklace in , where means that the final vertex of the -simplex is identified with the initial vertex of the -simplex, and the initial and final vertices of the necklace map to and respectively. A necklace is comprised of a sequence of beads, the above, that are strung together along the joins, defined to be the union of the initial and final vertices of each bead.
The necklace characterization
By a theorem of Dugger and Spivak, necklaces can be used to characterize the higher dimensional simplices of the hom-spaces as well, provided we keep track of additional vertex data.
Theorem (DS) Let be a simplicial set with vertices and . An -simplex in is uniquely represented by a triple , where is a necklace; is a map of simplicial sets that sends each bead of to a non-degenerate simplex of and the endpoints of the necklace to the vertices and respectively; and is a flag of sets of vertices of , where is the set of joins of .
Necklaces with the property described above are called totally non-degenerate. Note that the map need not be injective. If is a vertex with a non-degenerate edge , the map defines a totally non-degenerate necklace in .
Importantly, the face maps can also be described in the language of flags and necklaces. When , where is the flag of sets with removed from the sequence.
To compute , restrict to the subnecklace with vertices . If the triple is totally non-degenerate, this is the th face. Otherwise, there exists a unique quotient of that is totally non-degenerate, and , where is the image of under the surjection .
To compute , break up the beads of along the vertices in to form a necklace with joins ; we call this the -splitting of . If is totally non-degenerate, this is the 0th face. Otherwise, , the unique totally non-degenerate quotient, as above.
For example, let’s take and recompute . The vertices are necklaces whose set of joins must equal the set of vertices. These necklaces necessarily have the form and are in bijective correspondence with paths of 1-simplices from 0 to 3, as above.
The 1-simplices of are precisely the non-degenerate necklaces of from 0 to 3. They have shapes , , , (mapping to the 2-simplex ), (mapping to the 2-simplex ), , , , and , where these are listed in the same order given above (2).
Non-degenerate 2-simplices are necklaces together with a subset of vertices that strictly contains the set of joins. There are only two such, both with shape and flags or . It is a good exercise to compute the boundaries of these two 2-simplices to see which is which.
Applications
To my mind, a main selling point of the necklace characterization is that it makes it easy to compute the simplicial category associated to a generic simplicial set. (Exercise: compute the simplicial category associated to the -horn.) Even better, it allows us to easily prove a number of theorems.
The first result, describing the cofibrant replacement of an ordinary category regarded as a simplicial category with discrete hom-objects, might be known already, but I can’t find a reference. (Please tell me if you know one!)
Theorem. For any ordinary category , the simplicial category is equal to the simplicial category constructed by the comonad resolution described above (where is the ordinary nerve).
Proof: A necklace in a category is uniquely determined by its spine and the set of joins. An -simplex in the comonad resolution is a string of morphisms, each contained within sets of parentheses. The morphisms in the string describe the spine and the locations of each level of parentheses defines the corresponding set in the flag of vertex data.
When I started thinking about these things, I naively hoped that the simplicial categories associated to quasi-categories might have some fibrancy properties. Using the necklaces, we can prove:
Theorem. If is a quasi-category, any horn has a filler.
Proof: Amalgamate the two necklaces given by the horn, and then extend the resulting simplicial set to a larger necklace containing the two. This will determine the missing face and also the filler.
However, for most quasi-categories , indeed for all quasi-categories that are not themselves categories and then for many categories as well, there are some 3-dimensional inner horns (and likely also 4-dimensional horns) in some which cannot be filled. But in higher dimensions all horns (not necessarily inner) can be filled uniquely, as a consequence of the following Theorem, which really surprised me.
Theorem. For any simplicial set , is 3-coskeletal.
This says that any sphere in with at least four can be filled uniquely. The proof is actually quite easy. The necklace of the unique filler to a sphere also represents each of the inner faces and when , the flags of these faces also define the flag of the filler. It remains to check that this filler is compatible with the outer faces, but this can be done by considering the appropriate spherical identity.
When is a category, the hom-objects of are in fact 2-coskeletal. The main point of the proof is that the face map described in (3) is better behaved for necklaces in categories. Examples can be given to show that these results are all optimal, but I suspect I’ve said quite enough already.

Re: Understanding the homotopy coherent nerve
Thanks. Very interesting, indeed.
I am reading this in a bit of a hurry, since I really have to be looking into something else right now. But this bit here certainly looks very interesting:
You write:
Yes, that surprises me, too! :-)
Maybe one should emphasize at this point to the casual reader that is not in general a Kan complex, of course, and that the true hom--groupoid is the Kan fibrant replacement of this, which gives the true -categorical hom-object. These, then, will in general not be coskeletal anymore, hence will not be -groupoids for finite , in general.
All right, this is all I have time for right now. For the moment I added the link to your writeup to the page relation between quasi-categories and simplicial categories which I had been planning to fill with discussion along the lines of your exposition here, but never got around to yet.