The Strangest Numbers in String Theory
Posted by John Baez
Here’s a really easy introduction to normed division algebras, particularly the octonions, and their role in string theory. You basically just need to have gone to high school:
- John Baez and John Huerta, The strangest numbers in string theory, Scientific American, May 1, 2011, pp. 61-65.
Our contract with Scientific American let us put this version on our websites 3 months after publication.
If you want to see how Scientific American transformed our writing with top-notch editing but also added more of a pro-string-theory slant, you can compare the original.
For the details, see:
- John Huerta, Division Algebras, Supersymmetry and Higher Gauge Theory, Ph.D. thesis, U.C. Riverside, 2011.

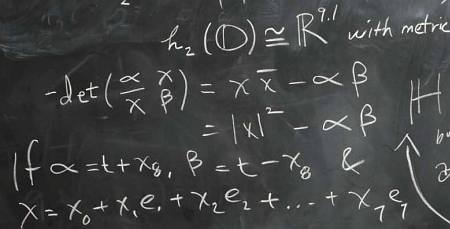

Re: The Strangest Numbers in String Theory
The article was intriguing, but John Huerta’s thesis with all the details looked a bit scary, or at least the kind of thing I’d need to spend six months on to really understand.
Here’s a naive question. The article seemed to imply that you might be able to construct an interaction Lagrangian between fermions and bosons in Riemannian 4-dimensional space by treating both as quaternions, and just multiplying them in the quaternionic way. But don’t you need a scalar for the Lagrangian?
I’ve recently been looking at four-dimensional Riemannian versions of the Proca and Dirac equations, but the interaction term between the Dirac spinors and the vector potential that I’ve been using is extremely similar to the Lorentzian one; it’s simply , as opposed to the Lorentzian (and the gamma matrices in the Riemannian version satisfy rather than ). One nice thing about the Riemmanian case is that is a scalar, because the representation of SO(4) on the Dirac spinors is unitary.
Anyway, if there’s a secret trick for combining a Dirac spinor and a vector as quaternions and getting a scalar, that would be fascinating to learn. But if I need to understand Lie-n-superalgebras first, I’d better put it off until I have a lot more free time!