A Math Puzzle Coming From Chemistry
Posted by John Baez
I posed this puzzle a while back over on Azimuth, and nobody solved it. Maybe it was too mathematical for most people there—it seems to be a problem in Klein geometry, actually. But also it’s a bit tricky: now that I think about it more, I’m not sure how to solve it either! ![]()
So, maybe you can help.
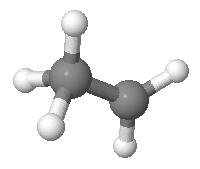
Suppose we have an ethyl cation. We’ll pretend it looks like this:
As I explained before, it actually doesn’t—not in real life. But never mind! Realism should never stand in the way of a good puzzle.
Continuing on in this unrealistic vein, we’ll pretend that the two black carbon atoms are distinguishable, and so are the five white hydrogen atoms. As you can see, 2 of the hydrogens are bonded to one carbon, and 3 to the other. We don’t care how the hydrogens are arranged, apart from which carbon each hydrogen is attached to. Given this, there are
ways to arrange the hydrogens. Let’s call these arrangements states.
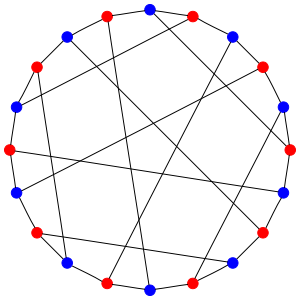
Now draw a dot for each of these 20 states. Draw an edge connecting two dots whenever you can get from one state to another by having a hydrogen hop from the carbon with 2 hydrogens to the carbon with 3. You’ll get this picture, called the Desargues graph:
The red dots are states where the first carbon has 2 hydrogens attached to it; the blue ones are states where the second carbon has 2 hydrogens attached to it. So, each edge goes between a red and a blue dot. And there are 3 edges coming out of each dot, since there are 3 hydrogens that can make the jump!
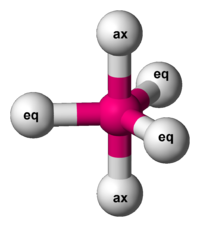
Now, the puzzle is to show that you can also get the Desargues graph from a different kind of molecule. Any molecule shaped like this will do:
The 2 balls on top and bottom are called axial, while the 3 around the middle are called equatorial.
There are various molecules like this. For example, phosphorus pentachloride. Let’s use that.
Like the ethyl cation, phosphorus pentachloride also has 20 states… but only if count them a certain way! We have to treat all 5 chlorines as distinguishable, but think of two arrangements of them as the same if we can rotate one to get the other. Again, I’m not claiming this is physically realistic: it’s just for the sake of the puzzle.
Phosphorus pentachloride has 6 rotational symmetries, since you can turn it around its axis 3 ways, but also flip it over. So, it has
states.
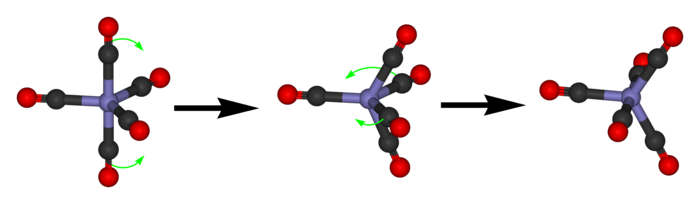
That’s good: exactly the number of dots in the Desargues graph! But how about the edges? We get these from certain transitions between states. These transitions are called pseudorotations, and they look like this:
Phosphorus pentachloride really does this! First the 2 axial guys move towards each other to become equatorial. Beware: now the equatorial ones are no longer in the horizontal plane: they’re in the plane facing us. Then 2 of the 3 equatorial guys swing out to become axial.
To get from one state to another this way, we have to pick 2 of the 3 equatorial guys to swing out and become axial. There are 3 choices here. So, we again get a graph with 20 vertices and 3 edges coming out of each vertex.
Puzzle. Is this graph the Desargues graph? If so, show it is.
I read in some chemistry papers that it is. But is it really? And if so, why? David Corfield suggested a promising strategy. He pointed out that we just need to get a 1-1 correspondence between
• states of the ethyl cation and states of phosphorus pentachloride,
together with a compatible 1-1 correspondence between:
• transitions of the ethyl cation and transitions of phosphorus pentachloride.
And he suggested that to do this, we should think of the split of hydrogens into a bunch of 2 and a bunch of 3 as analogous to the split of chlorines into a bunch of 2 (the ‘axial’ ones) and a bunch of 3 (the ‘equatorial’ ones).
It’s a promising idea. There’s a problem, though! In the ethyl cation, a single hydrogen hops from the bunch of 3 to the bunch of 2. But in a pseudorotation, two chlorines go from the bunch of 2 to the bunch of 3… and meanwhile, two go back from the bunch of 3 to bunch of 2.
And if you think about it, there’s another problem too. In the ethyl cation, there are 2 distinguishable carbons. One of them has 3 hydrogens attached, and one doesn’t. But in phosphorus pentachloride it’s not like that. The 3 equatorial chlorines are just that: equatorial. They don’t have 2 choices about how to be that way. Or do they?
Well, there’s more to say, but this should already make it clear that getting ‘natural’ one-to-one correspondences is a bit tricky… if it’s even possible at all!
We could try solving the problem using the ideas behind Felix Klein’s ‘Erlangen program’. The group of permutations of 5 things, say acts as symmetries of either molecule. For the ethyl cation the set of states will be for some subgroup You can think of as a set of structures of some sort on a 5-element set. The group acts on , and the transitions will give an invariant binary relation on . For phosphorus pentachloride we’ll have some set of states for some other subgroup , and the transitions will give an invariant relation on .
We could start by trying to see if is the same as —or more precisely, conjugate. If they are, that’s a good sign. And if not, it’s bad: it probably means there’s no ‘natural’ way to show the graph for phosphorus pentachloride is the Desargues graph… so maybe it’s not true.
I could say more, but I’ll stop here.


Re: A Math Puzzle Coming From Chemistry
You could and did – there was an extra sentence or two that you edited out from the Azimuth version!
You probably had your reasons… :-)