A Packing Pessimization Problem
Posted by John Baez
In a pessimization problem, you try to minimize the maximum value of some function:
For example: which convex body in Euclidean space is the worst for packing? That is, which has the smallest maximum packing density?
(In case you’re wondering, we restrict attention to convex bodies because without this restriction the maximum packing density can be made as close to as we want.)
Of course the answer depends on the dimension. According to Martin Gardner, Stanislaw Ulam guessed that in 3 dimensions, the worst is the round ball. This is called Ulam’s packing conjecture.
In 3 dimensions, congruent balls can be packed with a density of
and Kepler’s conjecture, now a theorem, says that’s their maximum packing density. So, Ulam’s packing conjecture says we can pack congruent copies of any other convex body in with a density above .
Ulam’s packing conjecture is still open. We know that the ball is a local pessimum for ‘centrally symmetric’ convex bodies in 3 dimensions. But that’s just a small first step.
Geometry is often easier in 2 dimensions… but in some ways, the packing pessimization problem for convex bodies in 2 dimensions is even more mysterious than in 3.
You see, in 2 dimensions the disk is not the worst. The disk has maximum packing density of
However, the densest packing of regular octagons has density
This is a tiny bit less! So, the obvious 2-dimensional analogue of Ulam’s packing conjecture is false.
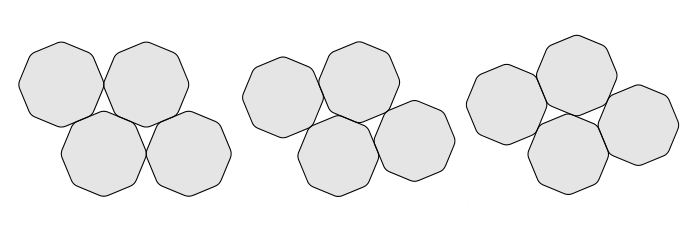
By the way, the densest packing of regular octagons is not the one with square symmetry:
It’s this:
which is closer in spirit to the densest packing of discs:
The regular octagon is not the worst convex shape for packing the plane! Regular heptagons might be even worse. As far as I know, the densest known packing of regular heptagons is this ‘double lattice’ packing:
studied by Greg Kuperberg and his father. They showed this was the densest packing of regular heptagons where they are arranged in two lattices, each consisting of translates of a given heptagon. And this packing has density
But I don’t know if this is the densest possible packing of regular heptagons.
Unlike the heptagon, the regular octagon is centrally symmetric: if we put its center at the origin, a point is in this region iff is in the region.
The great thing about convex centrally symmetric regions of the plane is that their densest packing is always a lattice packing: you take your region and form a packing by using all its translates where is a lattice. This is an old result of László Fejes Tóth and C. A. Rogers. For convex centrally symmetric regions, it reduces the search for the densest packing to a finite-dimensional maximization problem!
I said the regular octagon wasn’t the worst convex shape for densely tiling the plane. Then I said the regular heptagon might be worse, but I didn’t know. So what’s worse?
A certain smoothed octagon is worse:
Since it’s centrally symmetric, we know its densest packing is a lattice packing, so it’s not miraculous that someone was able to work out its density:
and the way it looks:
In fact this shape is believed to be the worst centrally symmetric convex region for densely packing the plane! I don’t really know why. But Thomas Hales, who proved the Kepler conjecture, has an NSF grant based on a proposal where he says he’ll prove this:
In 1934, Reinhardt considered the problem of determining the shape of the centrally symmetric convex disk in the plane whose densest packing has the lowest density. In informal terms, if a contract requires a miser to make payment with a tray of identical gold coins filling the tray as densely as possible, and if the contract stipulates the coins to be convex and centrally symmetric, then what shape of coin should the miser choose in order to part with as little gold as possible? Reinhardt conjectured that the shape of the coin should be a smoothed octagon. The smoothed octagon is constructed by taking a regular octagon and clipping the corners with hyperbolic arcs. The density of the smoothed octagon is approximately 90 per cent. Work by previous researchers on this conjecture has tended to focus on special cases. Research of the PI gives a general analysis of the problem. It introduces a variational problem on the special linear group in two variables that captures the structure of the Reinhardt conjecture. An interesting feature of this problem is that the conjectured solution is not analytic, but only satisfies a Lipschitz condition. A second noteworthy feature of this problem is the presence of a nonlinear optimization problem in a finite number of variables, relating smoothed polygons to the conjecturally optimal smoothed octagon. The PI has previously completed many calculations related to the proof of the Reinhardt conjecture and proposes to complete the proof of the Reinhardt conjecture.
This research will solve a conjecture made in 1934 by Reinhardt about the convex shape in the plane whose optimal packing density is as small as possible. The significance of this proposal is found in its broader context. Here, three important fields of mathematical inquiry are brought to bear on a single problem: discrete geometry, nonsmooth variational analysis, and global nonlinear optimization. Problems concerning packings and density lie at the heart of discrete geometry and are closely connected with problems of the same nature that routinely arise in materials science. Variational problems and more generally control theory are have become indispensable tools in many disciplines, ranging from mathematical finance to robotic control. However, research that gives an exact nonsmooth solution is relatively rare, and this feature gives this project special interest among variational problem. This research is also expected to further develop methods that use computers to obtain exact global solutions to nonlinear optimization problems. Applications of nonlinear optimization are abundant throughout science and arise naturally whenever a best choice is sought among a system with finitely many parameters. Methods that use computers to find exact solutions thus have the potential of finding widespread use. Thus, by studying this particular packing problem, mathematical tools may be further developed with promising prospects of broad application throughout the sciences.
I don’t have the know-how to guess what Hales will do. I haven’t even read the proof of that theorem by László Fejes Tóth and C. A. Rogers! It seems like a miracle to me.
But here are some interesting things that it implies.
Let’s say a region is a relatively compact open set. Just for now, let’s say a shape is a nonempty convex centrally symmetric region in the plane, centered at the origin. Let be the set of shapes. Let be the set of lattices in the plane, where a lattice is a discrete subgroup isomorphic to .
We can define a function
as follows. For each shape and lattice , if we rescale by a sufficiently small constant, the resulting shape will have the property that the regions are disjoint as ranges over . So, for small enough , will be a way of packing the plane by rescaled copies of . We can take the supremum of the density of over such , and call it
Thanks to the theorem of László Fejes Tóth and C. A. Rogers, the maximum packing density of the shape is
Here I’m taking advantage of the obvious fact that the maximum packing density of equals that of any rescaled version . And in using the word ‘maximum’, I’m also taking for granted that the supremum is actually attained.
Given all this, the pessimization problem for packing centrally symmetric convex regions is all about finding
But there’s more nice symmetry at work here. Linear transformations of the plane act on shapes, and lattices, and packings… and the concept of density is invariant under linear transformations!
One thing this instantly implies is that the maximum packing density for a centrally symmetric convex region doesn’t change if we apply a linear transformation to that region.
This is quite surprising. You might think that stretching or shearing a region could give a radically new way to pack it as densely as possible. And indeed that’s probably true in general. But for centrally symmetric convex regions, the densest packings are all lattice packings. So if we stretch or shear the region, we can just stretch or shear the lattice packing that works best, and get the lattice packing that works best for the stretched or sheared region. The packing density is unchanged!
We can say this using jargon. The group of linear transformations of the plane is . This acts on and , and for any we have
So, the function
is -invariant. And thus, the maximum packing density is invariant:
for all .
As mentioned before, we also have
where is any nonzero scalar multiple of the identity matrix (and thus a rescaling if ). So, we can replace by the quotient spaces , and work with
still acts on the first factor here, with scalar multiples of the identity acting trivially, and this map is still -invariant.
I think there should be a topology on that makes the quotient space compact and makes
continuous. Something like the Hausdorff metric, maybe. Can anyone help me here?
None of this goes far in solving the packing pessimization problem for convex centrally symmetric regions in the plane. We’ve reduced the number of degrees of freedom, but they’re still infinite.
But still, it’s fun. I like how it’s vaguely reminiscent of the theory of modular functions, which can be seen as -invariant functions of a lattice together with an ellipse centered at the origin.
References and Addenda
For more on packing pessimization problems, see:
- Yoav Kallus, Least efficient packing shapes.
To see who drew the pretty pictures, click on the pictures.
There’s a lot of good stuff in the comments. Most notably:
• The set has a nice topology making it a compact space. This is the moduli space of 2-dimensional real Banach spaces! In general, the moduli space of -dimensional real Banach spaces is called a Banach–Mazur compactum; click the link for details on its topology.
• Amazingly, there is a one-parameter family of maximally dense packings of the smoothed octagon! Greg Egan has made a movie showing all these packings:
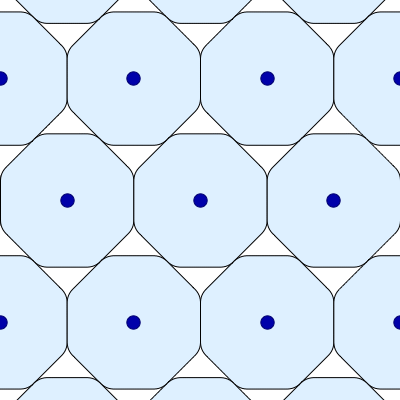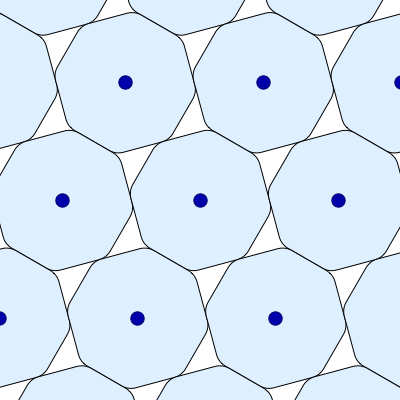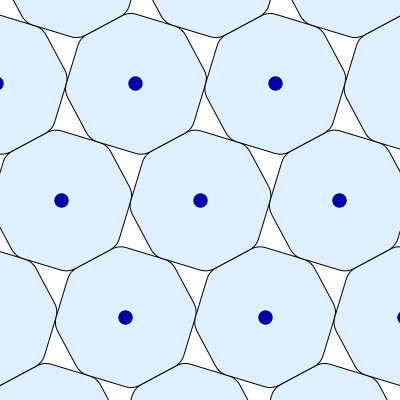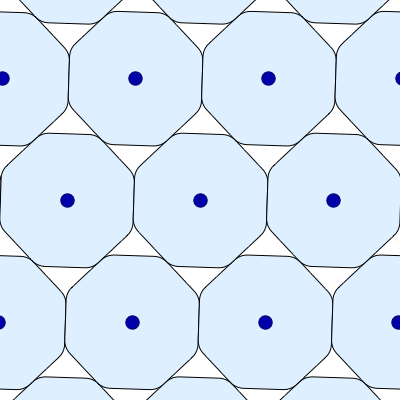
As the smoothed octagons turn, their centers move but the area in each space between them stays the same!


















Re: A Packing Pessimization Problem
The article “The 3-ball is a local pessimum for packing” is published here behind a paywall. But the arXiv version of the article is clearly more useful :-)