Integral Octonions (Part 7)
Posted by John Baez
Greg Egan and I have been thinking about Lorentzian lattices, and he just proved something nice about : it’s the lattice of self-adjoint matrices with integral octonions as entries!
This might be known already, but I’ve never seen it anywhere. So, let me show you the proof. But first, let me remind you why it matters.
If you missed the earlier parts of this series, you can see polished-up versions on my website:
-
Part 1: integral octonions and the Coxeter group E10. Also available here on the n-Category Café.

-
Part 2 - the integral octonions, 11d supergravity, and cosmological billiards. Also available here on the n-Category Café.
-
Part 3 - the 240 smallest integer octonions, also known as the E8 root polytope, and their connection to exceptional objects in mathematics. Also available here on the n-Category Café.

-
Part 4 - faces of the E8 root polytope. Also available here on the n-Category Café.
-
Part 5 - Dynkin diagrams and the geometry of the E8 root polytope. Also available here on the n-Category Café.
-
Part 6 - how to multiply octonions, and the Cayley integral octonions. Also available here on the n-Category Café.
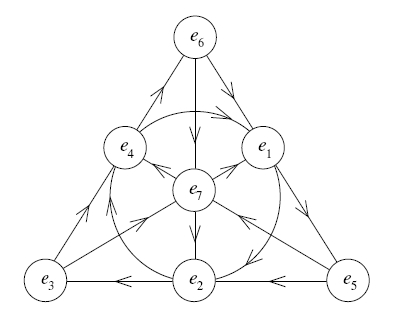
is the name of four related things:
- the unique lattice in 8-dimensional Euclidean space that is even (the dot product of any lattice vector with itself is even) and unimodular (the volume of each cell is 1),
- the finite group containing all reflections and rotations that are symmetries of this lattice,
- the simple Lie algebra that has this root lattice, and
- the Lie group that has this Lie algebra.
These things are endlessly absorbing, since they have deep connections to the icosahedron, the topology of 4-manifolds, string theory, and more. seems to be a wormhole in the fabric of mathematics, a portal that connects the most beautiful, special features of otherwise distant subjects.
For example: since the lattice lives in 8 dimensions, you can think of the vectors in this lattice as octonions! And if you rescale and rotate it correctly, this lattice becomes closed under octonion multiplication, as well as addition and subtraction. Then we call it the lattice of Cayley integers, or integral octonions:
is the octonions, and is the integral octonions.
I explained exactly how this works last time, in Part 6.
has a big brother called . Again this is the name of four things:
- the unique even unimodular lattice in 10-dimensional Minkowski spacetime,
- the infinite discrete group containing all reflections, rotations and Lorentz transformations that are symmetries of this lattice,
- the infinite-dimensional Lie algebra that has this root lattice, and
- the infinite-dimensional Lie group that has this Lie algebra.
It’s been known for a while that the symmetry group of the lattice has a nice description in terms of integral octonions:
- Axel Kleinschmidt, Hermann Nicolai, Jakob Palmkvist, Hyperbolic Weyl groups and the four normed division algebras.
Namely, the even part of this group, the transformations with determinant 1 rather than -1, is . Making sense of this group takes bit of work, since the octonions are nonassociative! But the paper above does it.
Recently Greg Egan and I have been thinking about this stuff, and a couple days ago he found something I’d long been hoping for: a description of the lattice itself in terms of integral octonions! It consists of self-adjoint matrices with entries in .
This is a discrete 10-dimensional analogue of a well-known 4-dimensional fact. Good old 4d Minkowksi spacetime can be seen as consisting of self-adjoint matrices with complex entries. Such matrices look like this:
with , and
is the Minkowski metric. The group acts on these self-adjoint matrices via
and this action preserves the determinant. So, we get a map from to the Lorentz group! The kernel of this is , so the group
is a subgroup of the Lorentz group, and in fact it’s the connected component of the identity:
The same sort of thing works for all four normed division algebras, though it gets kind of funky in the noncommutative and nonassociative cases:
The same idea should explain why is the even part of the symmetry group of the lattice. But implementing this demands that we see the lattice as consisting of matrices with entries in , the integral octonions.
We already know that 10-dimensional Minkowski spacetime is isometric to the space of self-adjoint octonionic matrices:
with its ‘Minkowski metric’
(You see, an octonion that’s its own conjugate can be identified with a real number.)
So, we want:
Theorem. Up to a rescaling, the lattice in 10-dimensional Minkowski spacetime is isometric to the set of self-adjoint matrices with integral octonions as entries: viewed as a sublattice of with its Minkowski metric.
Proof. Up to isometry, is the unique lattice in 10-dimensional Minkowski spacetime with a basis described by this Dynkin diagram:
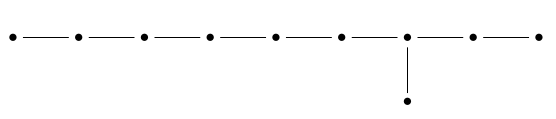
meaning that the basis vectors (called ‘simple roots’) have inner products
and for ,
when the corresponding dots in the diagram are connected by an edge, but
when they’re not. So, it suffices to find basis vectors for the lattice obeying identical relations up to rescaling, where the inner product is now the one coming from the Minkowski metric on .
Since the shortest nonzero vectors in have length 1, we need to rescale by a factor of . We thus seek 10 basis vectors for the lattice obeying
and for ,
when the corresponding dots in the Dynkin diagram are connected by an edge, but
otherwise.
Now, just as an octonion that’s its own conjugate can be identified with a real number, an integral octonion that is its own conjugate can be identified with an integer. So, we have
and
and in this description, the Minkowski metric is given by
Note that setting and to zero gives a way to identify any octonion with an element of , namely
This lets us identify any octonionic integer with an element of . The octonionic integers form a rescaled copy of the lattice. Since the Dynkin diagram for :
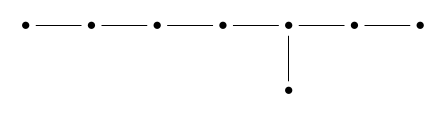
is contained in that for , a good first step is to find 8 choices for that correspond to rescaled versions of the simple roots for .
To do this, we identify with in such a way that the first component is real and the other seven components are imaginary, and the multiplication table is the one I described last time using this mnemonic:

Given all this, Egan chose these octonions as his rescaled versions of the simple roots for :
The diligent reader will check that each of these arises by taking a Kirmse integer (a concept explained last time) and swapping its first two coordinates, thus obtaining an element of . It is easy to see that each of these vectors has norm one:
But the diligent reader will also use this Dynkin diagram with its nodes numbered:
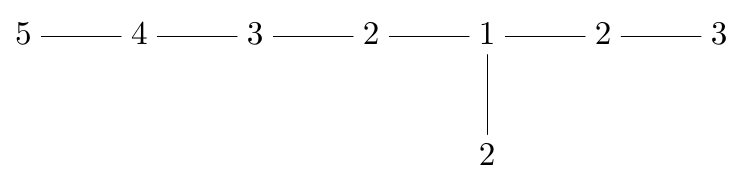
and verify that for we have
when the corresponding dots in the diagram are connected by an edge, but
otherwise.
Now we move up to 10 dimensions. We give a Minkowski metric where the first coordinate is timelike:
This allows us to identify and its Minkowski metric with as follows:
Next, we make the into vectors in by sticking two zero components onto the front of each one. Their inner products are unchanged. Thus, if we can find two more unit spacelike vectors with
and with all their other inner products with the being zero, we will have a full set of (rescaled) simple roots for sitting inside .
Here are two such vectors:
It is obvious that is orthogonal to , and not too hard to check that is orthogonal to and has .
So, now we have rescaled copies of the simple roots for , , all contained in . To complete the proof, it suffices to check that they are a basis for the lattice . To be precise: integer linear combinations of these vectors give the whole lattice.
One basis for consists of the matrices
for , along with two more matrices:
and
These two matrices correspond to the following vectors in , respectively:
So, we now have 10 vectors in that correspond to a basis of the lattice : , and corresponding to the first eight matrices. The only difference between this basis and the rescaled roots is that this basis includes rather than . But in fact we can write:
So the matrices that convert back and forth between the bases and both have integer entries, and we are done.
Of course, a more conceptual proof would be nice. I’m sure that will come in time. But for now I’m just basking in the warm glow of knowing this fact is true. It ties together a lot of things about the octonions, string theory in 10 dimensions, , and cosmological billiards in 11-dimensional supergravity!
In the current proof, a lot of work happens at the very last step. Personally, I got mixed up when checking this step. If you want to verify that
or in other words
this should help:
Just add up all the vectors on top and check that you get the one at the very bottom! Of course you should also check that I wrote down these vectors correctly.

Re: Integral Octonions (Part 7)
Here’s a new version of the key step in the proof that makes all the arithmetic go away.
with its usual normalisation is famously a unimodular lattice. That means that if we take a set of simple roots , and make them the columns of a matrix , we will have:
It follows that the Grammian matrix of dot products between the simple roots:
has determinant 1. Now, will have only integer entries (specifically, members of ), so with a determinant of 1 its inverse must also have only integer entries. Therefore the vector defined as:
will have only integer entries. Why does that matter? Well, if we’ve ordered our simple roots in the same way as the Dynkin diagram with numbered nodes that John has drawn in the article, what this is telling us is that the integer-linear combination of simple roots:
will have:
and for
In other words, we have shown that there is a point in the lattice itself that has the dot products we want in order to start extending the lattice towards the ten-dimensional version .
Of course our is an element of , and it uses the wrong normalisation for our present purposes where the lattice vectors have squared norm 1 rather than 2, but we can define:
where the are now construed as vectors in and have the correct normalisation. The crucial point is that the are integers.
The 10-dimensional form a basis of , along with:
So we can simply define:
Now it is plain that is an integer-linear combination of the basis vectors of that has the correct dot products with and in order for to comprise a set of simple roots whose Dynkin diagram is that of .