(For those for whom it is more convenient, a pdf of this post can be found here.)
Fantastic to see these posts! Apropos of not very much except the relevance of knot theory, I’d like to share some ideas I’ve been working on for a while. Any thoughts which anybody has would be most welcome. I’ve been kindly offered the possibility to write a guest post here about these ideas, but presenting the background in a pleasant way is a bit overwhelming. So instead I’m just going to present the ideas concisely here, and am happy to elaborate about anything.
What I’m going to talk about is to do with the Poincaré conjecture. The first reaction of any weather-beaten geometric topologist upon seeing these two words and seeing the simplicity and shortness of my arguments is probably going to be to dismiss them immediately! But I hope that one or two of you are generous and open-minded enough to have a think about them. Let me also try to bring things immediately down to earth. I did not set out to think about the Poincaré conjecture; I rather stumbled upon these ideas whilst discussing with a student, Reidun Persdatter Ødegaard, some work for her master thesis. If there is an error, there is an error; the ideas might be of some interest nevertheless. I would just ask that the argument be thought about on its own merits.
Enough of that! Let’s get down to it. I will first discuss what I like to call the ‘Poincaré conjecture for knots’. This is the following statement. Let be a framed knot (I will also denote by its associated blackboard framed knot diagram, and will switch between the two without mention). Let be the 3-manifold obtained by the integral Dehn surgery on determined by its framing. Then has trivial fundamental group if and only if is equivalent under the framed Reidemeister moves and Kirby moves to a framed unknot (a figure of eight).
What has this to do with the Poincaré conjecture? The latter says that any (closed) 3-manifold with trivial fundamental group is isomorphic to the 3-sphere. Any such 3-manifold is both connected and orientable. By a theorem of Lickorish and Wallace, for any (closed,) orientable, connected 3-manifold , there is a framed link such that is isomorphic to the 3-manifold obtained by the integral Dehn surgery on determined by its framing. Moreover, by a theorem of Kirby, a pair of such 3-manifolds and are isomorphic if and only if the corresponding blackboard framed link diagrams and can be obtained from one another by a finite sequence of framed Reidemeister moves and Kirby moves. Accurately or not, I like to think of these two results together as analogous to the surgery proof of the classification of surfaces. Anyhow, by taking the integral Dehn surgery on a -framed unknot with respect to its framing, we obtain the 3-sphere. Putting all this together, we see that the Poincaré conjecture can be reformulated as follows: if has trivial fundamental group, then the corresponding blackboard framed link diagram is equivalent under the framed Reidemeister moves and Kirby moves to the -framed unknot. What I am calling the Poincaré conjecture for knots is the special case where comes from an that is a framed knot.
In fact, we can go further, and reformulate the Poincaré conjecture as a statement purely in diagrammatic knot theory. Indeed, given and as in the previous paragraph, the fundamental group of is isomorphic to , the quotient of the fundamental group of by the normal subgroup generated by the longitude of . And both and can be defined from a link diagram. Thus the Poincaré conjecture becomes: if is a blackboard framed link diagram such that is trivial, then is equivalent under the framed Reidemeister moves and Kirby moves to a -framed unknot.
So far, all of this is background, well-known to geometric topologists. What I am going to do first is to give an argument to prove this last statement when is a blackboard framed knot diagram. And in fact, I am going to argue that, in this special case, no Kirby moves are needed. That is to say, I am going to give an argument to show that if is a blackboard framed knot diagram such that is trivial, then is equivalent under the framed Reidemeister moves alone to a -framed unknot. Thus we actually obtain something stronger than the Poincaré conjecture for knots: we also obtain the integral part of a theorem of Gordon and Luecke, that if we have a non-trivial (rational) Dehn surgery on a framed knot that gives the 3-sphere, then is isotopic to the unknot.
Begin, then, with a framed knot diagram . Equip it with an orientation (any will do), which is the one we will use to define its fundamental group and longitude. Label the arcs of . By a ‘word in the arcs of ’, I shall mean a monomial , where , , are (labels of) arcs of . I will say that a word in the arcs of is realisable if we can find a virtual knot which is equivalent to under the (virtual) framed Reidemeister moves, and which has the following property. First, if there are any occurrences of the longitude of as sub-words of , then remove them all except one. For ease of notation, I will suppose that we have already done this for . Then we ask that there is a point on such that as we walk around exactly once, in the direction defined by the orientation, beginning at and returning to , then we pass successively and in order under the arcs , \ldots, , and under no other arcs; and the power of is the sign (the usual one defined for a crossing of an oriented link diagram) of the crossing where we pass under .
Given a crossing of as follows (apologies for the ASCII figure, I hope that it displays correctly), I shall denote by the word in the arcs of .
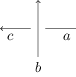
Now, is isomorphic to the quotient of the free group on the arcs of by the normal subgroup consisting exactly of words in the arcs of of the form and their inverses, where is any concatenation of copies of and of words in the arcs of of the form for various crossings of .
My key claim is that every word of of the form which contains a copy of is realisable, and moreover, if a word is equivalent to such a word of under the equivalence relation of being able to add or delete pairs and , where is an arc of , then is also realisable.
Let us prove this. Take any as above. Since we delete all copies of from except one when defining realisability, and since I am assuming that there is at least one copy of , we may assume that is of the form for some . We begin at . We will walk around in the same direction as our original orientation which we are using to define and . Suppose that looks as in the figure above. Take a small piece of the arc on which lies, just after . Drag it, using only virtual R2 moves, so that it is near the above figure. Then slide it (using two R2 moves and an R3 move) under the above crossing, so that we have the following local picture. If the arc on which lies has label , we label the arc indicated below of our new virtual knot diagram below by as well. In other words, we leave the labellings as they were, except that there is a ‘break’ in the arc labelled .
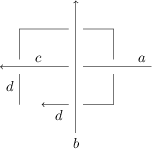
We now proceed in exactly the same way for , using the arc labelled in the above figure. And so on until we have done the same for . At this point, we now encounter in our word. And we now walk all the way around the virtual knot which we have obtained so far, from where we were after carrying out the above procedure for , stopping when we reach arc , a little before we reach . After this, we carry out the procedure above for , \ldots, , beginning with a little piece of arc between where we stopped and . After we are finished with , we simply walk to .
Hopefully you agree that this realises our !
Now, take the virtual knot that we have constructed to realise . To realise , where is any arc of , we proceed as follows. Take a small piece of the arc . Using virtual R2 moves, drag it across so that it is near the point . Then apply an R2 move so that we have the following local picture.
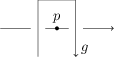
Walking around our new virtual knot from in the same direction as before, we have realised .
To establish the claim, it remains to show that if we add or delete a pair or , where is an arc of , from such a , then is also realisable. To add a pair between say and in , then we apply the same idea that we have just seen: take a small piece of the arc labelled on , drag it using virtual R2 moves so that it is near and , and then apply an R2 move so that we have the following picture.
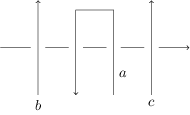
The same argument works for adding , just using the virtual R2 moves in a different way so that we can drag the arc over from the opposite side; and of course we could have or or both, and would be able to apply the same argument.
Suppose now that we wish to delete a pair from . Then we must successively walk first under and then under again in the opposite direction, without walking under any other arcs. This means that we have a local picture as follows, where there may be other arcs that pass under those shown or cross them virtually.
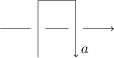
Using R2 and R3 moves and their virtual counterparts, we can slide the arc over the other depicted arc, so that we have (exactly, if we zoom in closely enough) the following local picture.
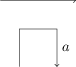
If we now walk around our new virtual knot in exactly the same way as before, beginning and ending at , we have cut out the pair. The same argument works for deleting a pair .
Hopefully you agree that the claim has been demonstrated! Now, what can we do with it?
Suppose that is trivial. Then is . Let be an arc of . Since is all of , we have that either or is equal in to a word of the form for some and , where is any concatenation of copies of and of words in the arcs of of the form for various crossings of .
My second claim is that for at least one arc of , the word in the word which is equal to either or contains at least one copy of . For if this is not the case, then every arc of or its inverse is equal in to a where is a product of ’s, that is to say, every arc of or its inverse is trivial in . But then is trivial, and no knot has a trivial fundamental group.
Combining the first and the second claim, we obtain that, for at least one arc of , we have that the word consisting just of or of is realisable. That is to say, there is a virtual knot which is equivalent to under the (virtual) R2 and R3 Reidemeister moves, and in which there is a point of from which, when we walk around in a particular direction and return back to , we pass only under a single arc, namely .
Every virtual knot diagram with a single (classical) crossing of the kind we obtain by our methods is equivalent under virtual R2 and R3 moves to a classical -framed unknot. Thus we deduce that is equivalent as a virtual knot under (virtual) R2 and R3 moves to a classical -framed unknot. But if a pair of classical knots are equivalent as virtual knots using (virtual) R2 and R3 moves, then they are equivalent as classical knots under the framed Reidemeister moves (this is an almost immediate consequence of the fact that the fundamental rack is a complete invariant of classical framed knots). We conclude that is equivalent as a classical knot under the framed Reidemeister moves to a -framed unknot, as required.
I would be delighted to hear what people think of this.
With some small adaptations, the same argument goes through for arbitrary links (not only knots) if a certain fact is true, to prove that if is trivial, where the ’s are the longitudes of the components of , then is equivalent under the framed Reidemeister moves and Kirby moves to the empty link. This is reformulation of the full Poincaré conjecture in diagrammatic knot theory. The Kirby moves are necessary here.
I will outline the necessary modifications. When defining realisability, we allow ourselves to delete copies of all longitudes, leaving only one copy of the longitude of one of the components, and no copies of the longitudes of any of the others. When constructing , we must take to be a point of an arc of the component of from which the single longitude in comes. At the very end of the argument, we use , for a pair of arcs and of , rather than for a single arc. (If there is only one arc of , then the result is trivial.) We then obtain that must be equivalent under (virtual) R2 and R3 moves to a virtual link which looks locally as follows (or with and switched).
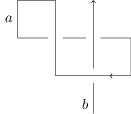
Now, the classical Kirby moves allow us to delete the component consisting of the arc . By induction on the number of components of , we conclude that must be equivalent under virtual framed Reidemeister moves and classical Kirby moves to the empty link diagram.
Now, I expect to be able to conclude here that must then be equivalent under classical framed Reidemeister moves and the classical Kirby moves to the empty link diagram. If this is true, we are done. However, as far as I know, no proof has yet been given that if a classical framed link diagram is equivalent under virtual framed Reidemeister moves and classical Kirby moves to another classical framed link diagram, then they are in fact equivalent under classical framed Reidemeister moves and classical Kirby moves.
A couple of words on the use of virtual knot theory in my argument: it allows us to drag a piece of an arc to another part of the knot diagram without affecting realisability. It is very difficult to see how to do this in general using only classical moves. The theorem that classical knots which are equivalent virtually are in fact equivalent classically is deep, because although it is a simple consequence of the fact that the fundamental rack is a complete invariant, the latter is a deep theorem.
Finally, a lot of people have very generously taken time, in some cases a lot of it, to think about earlier incarnations of these ideas. I’d especially like to thank Tobias Barthel, Emily Riehl, and Louis Kauffman. Richard Garner, Bruno Martelli, Markus Szymik, and Reidun Persdatter Ødegaard also gave, at various stages, feedback for which I’m very grateful.



 ,
,








Re: Globular for Higher-Dimensional Knottings
It’s great to see Globular starting to be used as a tool. If anyone hasn’t seen it in action, I recommend the video and other material here:
The video is from Jamie’s talk at the workshop on ‘Compositionality’ at the Simons Institute for the Theory of Computing. Since composition is something category theorists know a thing or two about, there were a lot of such people at this workshop, and a lot of fun talks, and a lot of great conversations. I’ve been blogging about these talks on Azimuth, and you can reach those blog articles (and more videos) starting here: