Star-autonomous Categories are Pseudo Frobenius Algebras
Posted by Mike Shulman
A little while ago I talked about how multivariable adjunctions naturally form a polycategory: a structure like a multicategory, but in which codomains as well as domains can involve multiple objects. Now I want to talk about some structures we can define inside this polycategory .
What can you define inside a polycategory? Well, to start with, a polycategory has an underlying multicategory, consisting of the arrows with unary target; so anything we can define in a multicategory we can define in a polycategory. And the most basic thing we can define in a multicategory is a monoid object — in fact, there are some senses in which this is the canonical thing we can define in a multicategory.
So what is a monoid object in ?
Well, actually it’s more interesting to ask about pseudomonoid objects, using the 2-categorical structure of . In this case what we have is an object , a (0,1)-variable adjunction (which, recall, is just an object ), and a (2,1)-variable adjunction , together with coherent associativity and unit isomorphisms. The left adjoint part of is a functor , and the associativity and unit isomorphisms then make into a monoidal category. And to say that this functor extends to a multivariable adjunction is precisely to say that is a closed monoidal category, i.e. that its tensor product has a right adjoint in each variable:
Similarly, we can define braided pseudomonoids and symmetric pseudomonoids in any 2-multicategory, and in these specialize to braided and symmetric closed monoidal categories.
Now, what can we define in a polycategory that we can’t define in a multicategory? The most obvious monoid-like thing that involves multiple objects in a codomain is a comonoid. So what is a pseudo-comonoid in ?
I think this question is easiest to answer if we use the duality of to turn everything around. So a pseudo-comonoid structure on a category is the same as a pseudo-monoid structure on . In terms of , that means it’s a monoidal structure that’s co-closed, i.e. the tensor product functor has a left adjoint in each variable:
The obvious next thing to do is to mix a monoid structure with a comonoid structure. In general, there’s more than one way to do that: we could think about bimonoids, Hopf monoids, or Frobenius monoids. However, while all of these can be defined in any symmetric monoidal category (or PROP), in a polycategory, bimonoids and Hopf monoids don’t make sense, because their axioms involve composing along multiple objects at once, whereas in a polycategory we are only allowed to compose along one object at a time.
Frobenius algebras, however, make perfect sense in a polycategory. If you look at the usual definition in a monoidal category, you can see that the axioms only involve composing along one object at once; when they’re written topologically that corresponds to the “absence of holes”.
So what is a pseudo Frobenius algebra in ? Actually, let’s ask a more general question first: what is a lax Frobenius algebra in ? By a lax Frobenius algebra I mean an object with a pseudo-monoid structure and a pseudo-comonoid structure, together with not-necessarily invertible “Frobenius-ator” 2-cells
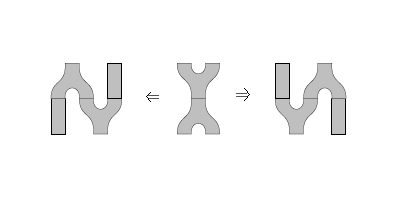
satisfying some coherence axioms, which can be found for instance in this paper (pages 52-55). This isn’t quite as scary as it looks; there are 20 coherence diagrams listed there, but the first 2 are the associativity pentagons for the pseudomonoid and pseudo-comonoid, while the last 8 are the unit axioms for the pseudomonoid and pseudo-comonoid (of which the and imply the other 6, by an old observation of Kelly). Of the remaining 10 axioms, 6 assert compatibility of the Frobenius-ators with the associativities, while 4 assert their compatibility with the units.
Now, to work out what a lax Frobenius algebra in is, we need to figure out what (2,2)-variable adjunctions those pictures represent. To work out what these functors are, I find it helpful to draw the monoid and comonoid structures with all the possible choices for input/output:
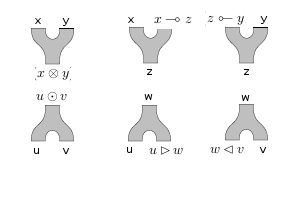
By the mates correspondence, to characterize a 2-cell in it suffices to consider one of the functors involved in the multivariable adjunctions, which means we should pick one of the copies of to be the “output” and consider all the others as the “input”. I find it easier to pick different copies of for the two Frobenius-ators. For the first one, let’s pick the second copy of in the codomain; this gives
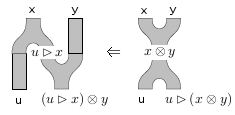
In the domain of the 2-cell, on the right, and come in and get combined into , and then that gets treated as and gets combined with coming in from the lower-left to give . In the codomain of the 2-cell, on the left, first gets combined with to give , then that gets multiplied with to give . Thus, the first Frobenius-ator is
For the second Frobenius-ator, let’s dually pick the first copy of in the codomain to be the output:
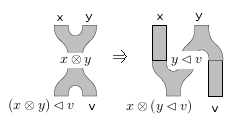
Thus the second Frobenius-ator is
What is this? Well, let’s take mates once with respect to the co-closed monoidal structure to reexpress both Frobenius-ators in terms of and . The first gives
and the second dually gives
These two transformations and have exactly the shape of the “linear distributivity” transformations in a linearly distributive category! (Remember from last time that linearly distributive categories are the “representable” version of polycategories.) The latter are supposed to satisfy their own coherence axioms, which aren’t listed on the nLab, but if you look up the original Cockett-Seely paper and count them there are… 10 axioms… 6 asserting compatibility with associativity of and , and 4 asserting compatibility with the unit. In other words,
A lax Frobenius algebra in is precisely a linearly distributive category! (In which is closed and is co-closed.)
Note that this is at least an approximate instance of the microcosm principle. (I have to admit that I have not actually checked that the two groups of coherence axioms coincide under the mates correspondence, but I find it inconceivable that they don’t.)
The next thing to ask is what a pseudo Frobenius algebra is, i.e. what it means for the Frobenius-ators to be invertible. If you’ve come this far (or if you read the title of the post) you can probably guess the answer: a -autonomous category, i.e. a linearly distributive category in which all objects have duals (in the polycategorical sense I defined in the first post).
First note that in a -autonomous category, is always closed and is co-closed, with and and so on. With these definitions, the Frobenius-ators become just associativity isomorphisms:
Thus, an -autonomous category is a pseudo Frobenius algebra in . Conversely, if is a pseudo Frobenius algebra in , then letting be the unit object of , we have
giving an isomorphism
Thus behaves like a dual of , and with a little more work we can show that it actually is. (I’m totally glossing over the symmetric/non-symmetric distinction here; in the non-symmetric case one has to distinguish between left and right duals, blah blah blah, but it all works.) So
A pseudo Frobenius algebra in is precisely a -autonomous category!
The fact that there’s a relationship between Frobenius algebras and -autonomous categories is not new. In this paper, Brian Day and Ross Street showed that pseudo Frobenius algebras in can be identified with “pro--autonomous categories”, i.e. promonoidal categories that are -autonomous in a suitable sense. In this paper Jeff Egger showed that Frobenius algebras in the -autonomous category Sup of suplattices can be identified with -autonomous cocomplete posets. And Jeff has told me personally that he also noticed that lax Frobenius algebras correspond to mere linear distributivity. (By the way, the above characterization of -autonomous categories as closed and co-closed linearly distributive ones such that certain transformations are invertible is due to Cockett and Seely.)
What’s new here is that the pseudo Frobenius algebras in are exactly -autonomous categories — not pro, not posets, not cocomplete.
There’s more that could be said. For instance, it’s known that Frobenius algebras can be defined in many different ways. One example is that instead of giving an algebra and coalgebra structure related by a Frobenius axiom, we could give just the algebra structure along with a compatible nondegenerate pairing . This is also true for pseudo Frobenius algebras in a polycategory, and in such a pairing corresponds to a contravariant self-equivalence , leading to the perhaps-more-common definition of star-autonomous category involving such a self-duality. And so on; but maybe I’ll stop here.

Re: Star-autonomous categories are pseudo Frobenius algebras
What I find fascinating about this is that, to the logician, polycategories are very appealing as they behave very much like sequents. But that’s not what is happening here: the polyarrows represent inference rules (several rules per polyarrow).
I can’t say I have quite wrapped my head around it yet. But it’s certainly appealing.