Categories of Nets (Part 2)
Posted by Mike Shulman
Now that John gave an overview of the Petri nets paper that he and I have just written with Jade and Fabrizio, I want to dive a bit more into what we accomplish. The genesis of this paper was a paper written by Fabrizio and several other folks entitled Computational Petri Nets: Adjunctions Considered Harmful, which of course sounds to a category theorist like a challenge. Our paper, and particularly the notion of -net and the adjunction in the middle column relating -nets to symmetric strict monoidal categories, is an answer to that challenge.
Suppose you wanted to “freely” generate a symmetric monoidal category from some combinatorial data. What could that data be? In other words (for a category theorist at least), what sort of category appears in an adjunction ? (By the way, all monoidal categories in this post will be strict, so I’m going to drop that adjective for conciseness.)
Perhaps the simplest choice is the same data that naturally generates a plain category, namely a directed graph. However, this is pretty limited in terms of what symmetric monoidal categories it can generate, since the generating morphisms will always only have single generating objects as their domain and codomain.
Another natural choice is the same data that naturally generates a multicategory, which might be called a “multigraph”: a set of objects together with, for every tuple of objects and single object , a set of arrows from to . In the generated symmetric monoidal category, such an arrow gives rise to a morphism ; thus we can now have multiple generating objects in the domains of generating morphisms, but not the codomains.
Of course, this suggests an even better solution: a set of objects, together with a set of arrows for every pair of tuples and . I’d be tempted to call this a “polygraph”, since it also naturally generates a polycategory. But other folks got there first and called it a “tensor scheme” and also a “pre-net”. In the latter case, the objects are called “places” and the morphisms “transitions”. But whatever we call it, it allows us to generate free symmetric monoidal categories in which the domains and codomains of generating morphisms can both be arbitrary tensor products of generating objects. For those who like fancy higher-categorical machinery, it’s the notion of computad obtained from the monad for symmetric monoidal categories.
However, pre-nets are not without flaws. One of the most glaring, for people who actually want to compute with freely generated symmetric monoidal categories, is that there aren’t enough morphisms between them. For instance, suppose one pre-net has three places and a transition , while a second pre-net has three places and a transition . Once we generate a symmetric monoidal category, then can be composed with a symmetry and similarly for ; so the symmetric monoidal categories generated by and are isomorphic. But there isn’t even a single map of pre-nets from to or vice versa, because a map of pre-nets has to preserve the ordering on the inputs and outputs. This is weird and annoying for combinatorial data that’s supposed to present a symmetric monoidal category.
Another way of making essentially the same point is that just as the adjunction between SMCs and directed graphs factors through categories, and the adjunction between SMCs and multigraphs factors through multicategories, the adjunction between SMCs and pre-nets factors through non-symmetric monoidal categories. In other words, a pre-net is really better viewed as data for generating a non-symmetric monoidal category, which we can then freely add symmetries to.
By contrast, in the objects that we call “Petri nets”, the domain and codomain of each generating morphism are elements of the free commutative monoid on the set of places — as opposed to elements of the free monoid, which is what they are for a pre-net. Thus, the domain of and above would be and respectively, which in a commutative monoid are equal (both are ). So the corresponding Petri nets of and are indeed isomorphic. However, once we squash everything down in this way, we lose the ability to functorially generate a symmetric monoidal category; all we can generate is a commutative monoidal category where all the symmetries are identities.
At this point we’ve described the upper row and the left- and right-hand columns in John’s diagram:
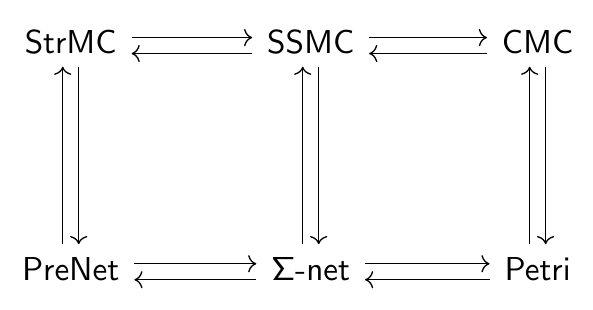
What’s missing is a kind of net in the middle that corresponds to symmetric monoidal categories. To motivate the definition of -net, consider how to solve the problem above of the “missing morphisms”. We want to send to a “permuted version” of . For this to be implemented by an actual set-map, we need this “permuted version” to be present in the data of somehow. This suggests that the transitions should come with a permutation action like that of, say, a symmetric multicategory. Then inside we can actually act on by the transposition , yielding a new morphism which we can take to be the image of . Of course, we can also act on by other permutations, and likewise on ; but since these permutation actions are part of the structure they must be preserved by the morphism, so sending to uniquely determines where we have to send all these permutation images.
Now you can go back and look again at John’s definition of -net: a set , a groupoid , and a discrete opfibration , where denotes the free-symmetric-strict-monoidal-category functor . Such a discrete opfibration is the same as a functor , and the objects of are the finite sequences of elements of while its morphisms are permutations; thus this is precisely a pre-net (the action of the functor on objects) with permutation actions as described above. I won’t get into the details of constructing the adjunction relating -nets to symmetric monoidal categories; you can read the paper, or maybe I’ll blog about it later.
However, in solving the “missing morphisms” problem, we’ve introduced a new possibility. Suppose we act on by the transposition that switches the first two entries. We get another transition with the same domain and codomain as ; so it might equal , or it might not! In other words, transitions in a -net can have isotropy. If , then when we generate a free symmetric monoidal category from our -net, the corresponding morphism will have the property that when we compose it with the symmetry morphism we get back again. No symmetric monoidal category generated by a pre-net has this property; it’s more like the behavior of the commutative monoidal category generated by a Petri net, except that in the latter case the symmetry itself is the identity, rather than just acting by the identity on .
This suggests that -nets can either “behave like pre-nets” or “behave like Petri nets”. This is made precise by the bottom row of adjunctions in the diagram. On one hand, we can map a pre-net to a -net by freely generating the action of all permutations. This has a right adjoint that just forgets the permutation action (which actually has a further right adjoint, although that’s a bit weird). On the other hand, we can map a Petri net to a -net by making all the permutations act as trivially as possible; this has a left adjoint that identifies each transition with all its permutation images. And these adjunctions commute with the three “free monoidal category” adjunctions in reasonable ways (see the paper for details).
The right adjoint mapping Petri nets into -nets is fully faithful, so we really can say that -nets “include” Petri nets. The left adjoint mapping pre-nets to -nets is not fully faithful — it can’t possibly be, since the whole point of introducing -nets was that pre-nets don’t have enough morphisms! But the full image of this functor is equivalent to a fourth kind of net: Kock’s whole-grain Petri nets. Kock’s approach to solving the problem of pre-nets is somewhat different, more analogous to the notion of “fat” symmetric monoidal category: he takes the domain and codomain of each transition to be a family of places indexed by a finite set. But his category turns out to be equivalent to the category of -nets that are freely generated by some pre-net. (Kock actually proved this himself, as well as sketching the adjunction between -nets and symmetric monoidal categories. He called -nets “digraphical species”.)
So -nets “include” both Petri nets and pre-nets, in an appropriate sense. The pre-nets (or, more precisely, whole-grain nets) are the -nets with free permutation actions (trivial isotropy), while the Petri nets are the -nets with trivial permutation actions (maximal isotropy). In Petri-net-ese, these correspond to the “individual token philosophy” and the “collective token philosophy”, respectively. (This makes it tempting to refer to the functors from -nets to pre-nets and Petri nets as individuation and collectivization respectively.) But -nets also allow us to mix and match the two philosophies, having some transitions with trivial isotropy, others with maximal isotropy, and still others with intermediate isotropy.
I like to think of -nets as a Petri net analogue of orbifolds. Commutative-monoid-based Petri nets are like “coarse moduli spaces”, where we’ve quotiented by all symmetries but destroyed all the isotropy information; while whole-grain Petri nets are like manifolds, where we have no singularities but can only quotient by free actions. Pre-nets can then be thought of a “presentation” of a manifold, such as by a particular way of gluing coordinate patches together: useful in concrete examples, but not the “invariant” object we really want to study mathematically.

Re: Categories of Nets (Part 2)
Anything interesting to say about the (co)monads produced on -net? Any modalities about?