Large Sets 1
Posted by Tom Leinster
Next: Part 2
This is the first of a series of posts on how large cardinals look in categorical set theory.
My primary interest is not actually in large cardinals themselves. What I’m really interested in is exploring the hypothesis that everything in traditional, membership-based set theory that’s relevant to the rest of mathematics can be done smoothly in categorical set theory. I’m not sure this hypothesis is correct (and I suppose no one could ever be sure), which is why I use the words “hypothesis” and “explore”. But I know of no counterexample.
These posts won’t assume very much knowledge of anything. And I’ll try to stick to one topic per post. In this first one, all I’ll do is clear my throat.
There are three differences between what I’ll do here and what you’ll find in almost all books on set theory.
First, I’ll be using a style of set theory that so far I’ve been calling categorical, and which could also be called isomorphism-invariant or structural, but which I really want to call neutral set theory.
What I mean is this. In cooking, a recipe will sometimes tell you to use a neutral cooking oil. This means an oil whose flavour is barely noticeable, unlike, say, sesame oil or coconut oil or extra virgin olive oil. A neutral cooking oil fades into the background, allowing the other flavours to come through.
The kind of set theory I’ll use here, and the language I’ll use to discuss it, is “neutral” in the sense that it’s the language of the large majority of mathematical publications today, especially in more algebraic areas. It’s the language of structures and substructures and quotients and isomorphisms, the lingua franca of algebra. To most mathematicians, it should just fade into the background, allowing the essential points about sets themselves to come through.
Some readers might want to call this language “categorical”, but that wouldn’t be quite right: it’s precategorical, the kind of thing that undergraduates get used to in early courses on abstract algebra — when they first learn about groups or rings or vector spaces, well before they’re likely to see a category. And in my posts, I’ll mention categories only occasionally.
“Neutral” doesn’t mean that no one can object. (Theorem: for all things, there exists a person who objects to that thing.) Someone is sure to say it would taste better with sesame or ZFC. But the point is that you can add that flavour if you want.
For example, consider ordinals.
In ZFC, is a binary relation defined on the collection of all sets. Every element of every set is also a set, and for any two sets and , one can ask whether . It follows that restricts to a binary relation on any individual set .
In the classical approach to set theory, an ordinal is defined to be a set satisfying certain properties. These properties imply that the relation on is a well ordering. They also imply that every well-ordered set is isomorphic to for precisely one ordinal . In other words, the ordinals are representatives of the isomorphism classes of well-ordered sets.
Some people like the classical definition of ordinal, some don’t. Neutral set theory takes no position. Nothing we’ll do is incompatible with defining the ordinals as above and showing that they’re representatives for the iso classes of well-ordered sets. But equally, nothing we’ll do requires the classical notion of ordinal. We’re just going to talk about well-ordered sets themselves, directly.
In general, I’ll be talking about sets and sets with structure and functions and subsets and relations and families and so on, using the same language that appears in hundreds of math papers published every day. They’re blog posts, so I’ll be writing informally. But the formal axiom system that everything will be based on is Lawvere’s Elementary Theory of the Category of Sets (ETCS).
In categorical jargon, ETCS states that the category of sets is a well-pointed topos with a natural numbers object and choice. In informal language, it says we have some things called “sets”, some things called “functions from to ” for each set and set , and an operation of “composition” on functions, satisfying the following axioms:
- Composition of functions is associative and has identities.
- There is a set with exactly one element.
- There is a set with no elements.
- A function is determined by its effect on elements.
- Given sets and , one can form the cartesian product .
- Given sets and , one can form the set of functions from to .
- Given and , one can form the inverse image .
- The subsets of a set correspond to the functions from to .
- The natural numbers form a set.
- Every surjection has a right inverse.
I said that this is an informal phrasing of the axioms. You can find the formal (but elementary) version here, for instance. But in case your desire to understand these axioms is not quite great enough to make you want to click that link, I give you a kind of FAQ:
Many of the axioms (2, 5, 6, 7, 8 and 9) involve universal properties. For instance, axiom 5 states that for any two sets and , there is a diagram with the universal property of a product.
In particular, axiom 2 states that there is a terminal set (a set with the property that for every set , there is exactly one function ). Since being a terminal set is a universal property, any two terminal sets are isomorphic, and I’ll write for any of them.
An element of a set is defined to be a function . So, “” means . (In particular, has exactly one element.) When the axioms refer to “elements”, that’s what’s meant.
Axiom 8 actually says that there’s some set with the property that for any set , the subsets of correspond to the functions . As it turns out, the other axioms imply that has exactly two elements.
While everyone agrees that the elements of a set are in canonical one-to-one correspondence with the functions , some people don’t like defining an element of to literally be a function . That’s OK. True to the spirit of neutral set theory, I’ll never rely on this definition of element. All we’ll need is that uncontroversial one-to-one correspondence.
The most important thing in all of this, the thing that separates it from the dominant ZFC-based approach, is that we won’t assume that elements of a set are sets, or that one can ask “is ?” of any two sets and . It simply won’t be necessary.
At the beginning, I said that what we’ll do in these posts differs from the norm in three ways. That was just the first!
The second is more superficial: instead of talking about large cardinals, I’ll talk about large sets.
Categorical set theory doesn’t have much use for the noun “cardinal”. In the classical ZFC-based approach, a cardinal is defined to be an ordinal with a certain property, and one can prove that every set is isomorphic to (in bijection with) precisely one cardinal. So, the cardinals are representatives of the isomorphism classes of sets. But in an isomorphism-invariant approach to set theory, there’s no need to choose representatives. We just work directly with sets.
If “cardinal” means anything in categorical set theory, it means isomorphism class of sets. Now and again I’ll use the word that way, e.g. when I want to talk about the set of cardinals smaller than a given set. But almost always, I’ll just talk about sets.
The situation is the same as in group theory, for instance. We don’t often need to say “isomorphism class of groups”. We just say “group”. (“There are two groups of order four.”) This is safe because all properties of groups are isomorphism-invariant. The same goes for sets.
It takes a while to get used to saying things like “inaccessible set” when the rest of the world says “inaccessible cardinal”. But now that I’m used to replacing “cardinal” by “set”, “cardinal” is starting to sound a bit arcane. Why would you use this special word for an isomorphism class of sets — or an ingeniously constructed representative of it — when the property of sets you’re talking about is isomorphism-invariant anyway? You don’t do this for groups or any other type of mathematical structure. So why do you do it for sets?
The third and final feature that makes these posts different is that ETCS is a weaker set theory than ZFC. Fewer things are true in it.
If by “large set” (or “large cardinal”) we mean one whose existence is not guaranteed by our axiom system, then more sets are large in ETCS than in ZFC. In other words, ZFC has higher standards for calling something large. (“That’s not a large set, that’s a large set”.)
Roughly speaking, the way this series of posts will work is that I’ll start with the smallest “large sets” and work my way upwards. The first half or so of the series will be entirely about sets that are large relative to ETCS but not relative to ZFC — that is, ZFC guarantees their existence but ETCS doesn’t. There are several intermediate stages. Personally, I feel like I understand the difference between the two theories better now that I’ve got this picture clear in my head.
Postscript: are category theorists interested in weak set theories?
As I understand it, some set theorists have the impression that category theorists are particuarly attached to set theories that are weaker than ZFC. Is that true?
The fact of the matter is that ETCS is weaker than ZFC. Whether you call it slightly weaker or vastly weaker is a matter of perspective. On the one hand, it’s thought that all of EGA, SGA, and probably the proof of Fermat’s last theorem can be done in ETCS. Most mathematicians will never need more than ETCS provides. So for practical purposes, you might say there’s not much difference between ETCS and ZFC. But to a professional set theorist, this probably sounds as absurd as the argument “hardly anyone ever uses integers bigger than , so there’s not much difference between and .”
ETCS is not the only categorical set theory. In particular, it’s very natural to add to it an axiom scheme of replacement (a kind of cocompleteness condition, which I’ll come to in a later post). The resulting theory, “ETCS+R”, is equivalent to ZFC in the strongest possible sense: the two theories are biinterpretable. This means that there’s a way of translating statements in the language of ETCS+R into statements in the language of ZFC, and vice versa, such that the two translation processes are mutually inverse and make theorems of ETCS+R match up with theorems of ZFC. In particular, ETCS+R is a categorical set theory exactly as strong as ZFC.
But if we’re honest, category theorists don’t often add this axiom scheme of replacement. Natural as it is, it has a different flavour from the other axioms of ETCS. We do tend to focus on a set theory weaker than ZFC.
Still, something doesn’t ring true to me about the idea that category theorists are interested in, or attached to, weak set theories. Here’s what I think is going on.
Category theorists are interested in much more than just categories of sets. There are categories of many kinds, and we want to be able to move between them. A set can be viewed as a degenerate kind of space (with no geometric structure), or a degenerate kind of algebra (with no operations or equations), or a degenerate kind of sheaf (a sheaf on the one-point space):
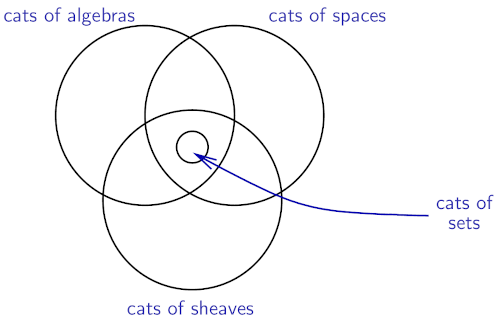
For any given fact about sets, it’s categorically natural to ask whether that fact holds in a wider context than just categories of sets. Maybe it’s true in all toposes, or all cartesian closed categories, or all categories of algebras for an algebraic theory. That’s the kind of question that category theorists ask. It’s not so much that we’re aiming to use a set theory that’s as weak as possible, but that we want to find the right level of generality for everything. And that generality may go far beyond the world of sets.
To put it another way, imagine a mathematician who studies categories of algebras (for finitary algebraic theories, say). Since sets are the algebras for a certain trivial algebraic theory, anything that’s true of all categories of algebras is true of . But it would be perverse to say that our imaginary mathematician is doing “weak set theory”. It would be like describing the class of mammals as “generalized platypuses”.
I think that’s the answer. Category theorists are not a priori interested in set theories that are weak; we’re interested in worlds beyond sets.
Next time
In part 2, I’ll get started on the smallest kind of large set: limits.

Re: Large Sets 1
If ETCS + Replacement is biinterpretable with ZFC, then what categorical/topos theoretic set theory is biinterpretable with classical ZF?