Schur Functors and Categorified Plethysm

June 2, 2021

Schur Functors and Categorified Plethysm

Posted by John Baez

$MathML-enabled post (click for more details).$

It’s done!

John Baez, Joe Moeller and Todd Trimble, Schur functors and categorified plethysm.

This paper has been 14 years in the making. So let me tell you a bit of its history, and then I’ll explain the paper itself.

$MathML-enabled post (click for more details).$

The history

This paper got its start in April 2007 when Allen Knutson raised a question about Schur functors here on the $n$ -Category Café. I conjectured an answer, and later Todd Trimble refined the conjecture and proved it. We had this written up on the nLab by July 2010. At this point we knew exactly why the category of Schur functors is a categorified version of $\mathbb{Z}[x]$ , the polynomials in one variable.

Then came a long pause. I went to Singapore for 2 years and started work on applied category theory. When I came back to California, I worked with grad students only on that subject.

In 2015 Joe Moeller became a grad student at U. C. Riverside. He did applied category theory, but he had a strong interest in pure math, so after his thesis was mostly done we decided to start a side-project on representation theory. We knew that the Grothendieck group of the category of Schur functors is the ring of symmetric functions. This ring has a lot of structure: like $\mathbb{Z}[x]$ , it’s something called a plethory. It seemed clear that most of this structure comes from the category of Schur functors, which should thus be some sort of categorified plethory. We began to work out the details around February 2020.

Todd Trimble rejoined the project roughly around June of that year. Since then he’s been the idea engine, pushing the paper to completion. This paper is the result.

Schur functors and categorified plethysm

The symmetric groups $S_n$ play a distinguished role in group theory, and their representations are rich in structure. Much of this structure only reveals itself if we collect all these groups into the groupoid $\mathsf{S}$ of finite sets and bijections. Let $\mathsf{Fin}\mathsf{Vect}$ be the category of finite-dimensional vector spaces over a field $k$ of characteristic zero. A functor $\rho \colon \mathsf{S} \to \mathsf{Fin}\mathsf{Vect}$ simply amounts to a (possibly infinite) direct sum of representations of the groups $S_n$ . Our focus is on $\mathsf{Schur}$ , the full subcategory of $\mathsf{Fin}\mathsf{Vect}^\mathsf{S}$ consisting of finite direct sums of finite-dimensional representations.

This category $\mathsf{Schur}$ binds all the finite-dimensional representations of all the symmetric groups $S_n$ into a single entity, revealing more structure than can be seen working with these groups one at a time. In particular, $\mathsf{Schur}$ has a monoidal structure called the ‘plethysm’ tensor product, with respect to which $\mathsf{Schur}$ acts on the category $\mathsf{Rep}(G)$ of representations of any group $G$ . Each object of $\mathsf{Schur}$ acts as an endofunctor of $\mathsf{Rep}(G)$ called a ‘Schur functor’. Thus, $\mathsf{Schur}$ plays a fundamental role in representation theory, which we aim to clarify.

We also apply our results on $\mathsf{Schur}$ to study the ring of symmetric functions, denoted $\Lambda$ . This ring shows up in many guises throughout mathematics. For example:

It is the Grothendieck group of the category $\mathsf{Schur}$ .
It is the subring of $\mathbb{Z}[[x_1, x_2, \dots]]$ consisting of power series of bounded degree that are invariant under all permutations of the variables — hence the name symmetric functions.
It is the cohomology ring $H^*(BU)$ , where $BU$ is the classifying space of the infinite-dimensional unitary group.

As a mere ring, $\Lambda$ is not very exciting: it is isomorphic to a polynomial ring in countably many generators. But $\Lambda$ is richly endowed with a plethora of further structure. In his excellent review article, Hazewinkel gushed:

It seems unlikely that there is any object in mathematics richer and/or more beautiful than this one [….]

Following ideas of Tall and Wraith, Borger and Wieland defined a concept of ‘plethory’ (which we call ‘ring-plethory’) that encapsulates much of this rich structure on $\Lambda$ . Here we derive the ring-plethory structure on $\Lambda$ from a ‘2-plethory’ structure on $\mathsf{Schur}$ , of which $\Lambda$ is the Grothendieck group. More than merely proving that $\Lambda$ is a ring-plethory, this shows that much of its rich structure exists at a higher level in the category of Schur functors.

What is a ring-plethory? To understand this, it is good to start with the simplest example of all, $\mathbb{Z}[x]$ , the ring of polynomials with integer coefficients in one variable. (Following the algebraic geometers, we use ‘ring’ to mean ‘commutative ring with unit’.) $\mathbb{Z}[x]$ is the free ring on one generator. But besides the usual ring operations, $\mathbb{Z}[x]$ also has ‘co-operations’ that act like ring operations going backwards. These are all derived by exploiting the freeness property. Namely, $\mathbb{Z}[x]$ is equipped with the unique ring homomorphisms that send $x$ to the indicated elements:

coaddition: $\begin{array}{rrcl} \alpha \colon &\mathbb{Z}[x] &\to& \mathbb{Z}[x] \otimes \mathbb{Z}[x] \\ &x & \mapsto& x \otimes 1 + 1 \otimes x \end{array}$
co-zero: $\begin{array}{rrcl} o \colon &\mathbb{Z}[x] &\to& \mathbb{Z} \\ &x & \mapsto & 0 \end{array}$
co-negation: $\begin{array}{rrcl} \nu \colon & \mathbb{Z}[x] &\to& \mathbb{Z}[x] \\ &x & \mapsto& - x \end{array}$
comultiplication: $\begin{array}{rrcl} \mu \colon& \mathbb{Z}[x] &\to& \mathbb{Z}[x] \otimes \mathbb{Z}[x] \\ &x & \mapsto& x \otimes x \end{array}$
co-one: $\begin{array}{rrcl} \epsilon \colon &\mathbb{Z}[x] &\to& \mathbb{Z} \\ &x & \mapsto& 1 \end{array}$

These obey all the usual ring axioms if we regard them as morphisms in the opposite of the category of rings. Thus we say $\mathbb{Z}[x]$ is a biring: a ring object in $\mathsf{Ring}^{\mathrm{op}}$ .

Why is $\mathbb{Z}[x]$ a biring? Any ring can be seen as the ring of functions on some kind of space, and $\mathbb{Z}[x]$ is the ring of functions on the affine line, $\mathbb{A}^1$ . Grothendieck made this into a tautology by defining the category of affine schemes to be $\mathsf{Ring}^{\mathrm{op}}$ and defining $\mathbb{A}^1$ to be the ring $\mathbb{Z}[x]$ seen as an object in $\mathsf{Ring}^{\mathrm{op}}$ . But the affine line itself can be made into a ring, much like the real or complex line. Thus $\mathbb{A}^1$ becomes a ring object in the category of affine schemes. But this is precisely a biring! The formulas above express the ring operations on $\mathbb{A}^1$ as co-operations on $\mathbb{Z}[x]$ .

A biring can equivalently be seen as a ring $B$ such that the representable functor

$\mathsf{Ring}(B, -) \colon \mathsf{Ring} \to \mathsf{Set}$

is equipped with a lift to a functor $\Phi_B$ taking values in the category of rings, like this:

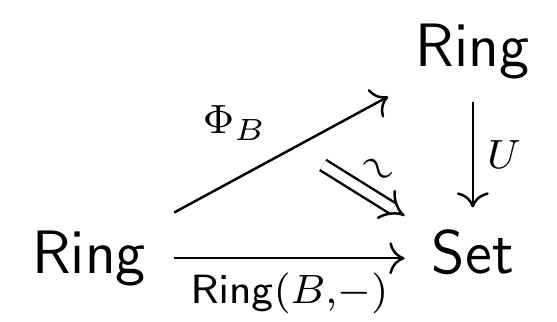
Given a biring $B$ , the co-operations on $B$ give $\mathsf{Ring}(B, R)$ a ring structure for any ring $R$ in a way that depends functorially on $R$ . For example, since $\mathbb{Z}[x]$ is the free ring on one generator, $\mathsf{Ring}(\mathbb{Z}[x], -)$ assigns to any ring its underlying set. Thus $\mathsf{Ring}(\mathbb{Z}[x], -)$ lifts to the identity functor on $\mathsf{Ring}$ . This gives $\mathbb{Z}[x]$ a natural biring structure, and one can check that this is the one described above.

This second viewpoint is fruitful because endofunctors on $\mathsf{Ring}$ can be composed. Though not all endofunctors on $\mathsf{Ring}$ are representable, those that are representable are closed under composition. Thus for any birings $B$ and $C$ there is a biring $B \odot C$ such that

$\Phi_C \circ \Phi_B \cong \Phi_{B \odot C}$

This puts a monoidal structure $\odot$ on the category $\mathsf{Biring}$ , called the composition tensor product. A ring-plethory is then a monoid object in $(\mathsf{Biring}, \odot)$ . Since the category $\Biring$ is defined as the opposite of the category of ring objects in $\mathsf{Ring}^{\mathrm{op}}$ , $B$ is a ring-plethory when $\Phi_B$ is a comonad.

For example, since $\mathsf{Ring}(\mathbb{Z}[x], -)$ lifts to the identity functor on $\mathsf{Ring}$ , and the identity functor is a comonad, $\mathbb{Z}[x]$ with the resulting biring structure is a ring-plethory. Concretely, this ring-plethory structure on $\mathbb{Z}[x]$ simply captures the fact that one can compose polynomials in one variable.

A more interesting ring-plethory is $\Lambda$ , the ring of symmetric functions. This structure is often described in terms of fairly elaborate algebraic constructions. It seems not to be generally appreciated that there is a conceptual explanation for all this structure. Our goal is to provide that explanation.

We achieve this by categorifying the story so far, developing a theory of 2-plethories, and showing that $\mathsf{Schur}$ is a 2-plethory. Using this fact we show that $\Lambda$ , the Grothendieck group of $\mathsf{Schur}$ , is a ring-plethory.

Before doing this, we must categorify the concepts of ring and biring. Or rather, since it is problematic to categorify subtraction directly, we start by omitting additive inverses and work not with rings but with rigs, which again we assume to be commutative. A birig is then a rig object in the opposite of the category of rigs. For example, the free rig on one generator is $\mathbb{N}[x]$ , and this becomes a birig with co-operations defined just as for $\mathbb{Z}[x]$ above — except for co-negation.

The concept of plethory also generalizes straightforwardly from rings to rigs. In fact it generalizes to algebras of any monad $M$ on $\mathsf{Set}$ . Stacey and Whitehouse called such a generalized plethory a ‘Tall–Wraith monoid’, but we prefer to call it an M-plethory in order to refer to various specific monads $M$ . If $M$ is the monad whose algebras are rings, then $M$ -plethories are ring-plethories, but when $M$ is the monad for rigs, we call an $M$ -plethory a rig-plethory. For example, just as $\mathbb{Z}[x]$ becomes a ring-plethory, $\mathbb{N}[x]$ becomes a rig-plethory. This captures the fact that we can compose polynomials in $\mathbb{N}[x]$ .

There are various ways to categorify the concept of rig. Since our goal is to study Schur functors and some related classical topics in representation theory, we shall fix a field $k$ of characteristic zero and define — just for the purposes of this paper — a ‘2-rig’ to be a symmetric monoidal Cauchy complete linear category. In more detail:

A linear category is an essentially small category enriched over $\mathsf{Vect}$ , the category of vector spaces over $k$ .
A linear category is Cauchy complete when it has biproducts and all idempotents split.
A symmetric monoidal linear category is a linear category with a symmetric monoidal structure for which the tensor product is bilinear on hom-spaces.
A 2-rig is a symmetric monoidal linear category that is also Cauchy complete.

In language perhaps more familiar to algebraists, a linear category is Cauchy complete when it has finite direct sums and any idempotent endomorphism has a cokernel. In this definition of 2-rig we do not need to impose a rule saying that the tensor product preserves biproducts and splittings of idempotents in each argument, since this is automatic: these are ‘absolute’ colimits for linear categories, meaning they are preserved by any linear functor. This absoluteness is one of the virtues of demanding only Cauchy completeness rather a larger class of colimits.

With this definition, $\mathsf{Schur}$ turns out to be the free 2-rig on one generator. Many other important categories are also 2-rigs:

the category $\mathsf{Fin}\mathsf{Vect}$ of finite-dimensional vector spaces over $k$ ,
the category of representations of any group on finite-dimensional vector spaces,
the category of finite-dimensional $G$ -graded vector spaces for any group $G$ ,
the category of bounded chain complexes of finite-dimensional vector spaces,
the category of finite-dimensional super vector spaces,
for $k = \mathbb{R}$ or $\mathbb{C}$ , the category of finite-dimensional vector bundles over any topological space, or smooth vector bundles over any smooth manifold,
the category of algebraic vector bundles over any algebraic variety over $k$ ,
the category of coherent sheaves of finite-dimensional vector spaces over any algebraic variety (or scheme or algebraic stack) over $k$ .

Some of these categories are abelian, but categories of vector bundles are typically not. They are still Cauchy complete, and this is another reason we develop our theory at this level of generality.

There is a 2-category of 2-rigs, denoted $\mathbf{2Rig}$ , and we define a 2-birig to be a 2-rig $\mathsf{B}$ such that the 2-functor $\mathbf{2Rig}(\mathsf{B}, -) \colon \mathbf{2Rig} \to \mathbf{Cat}$ is equipped with a lift to a 2-functor $\Phi_\mathsf{B}$ taking values in 2-rigs:

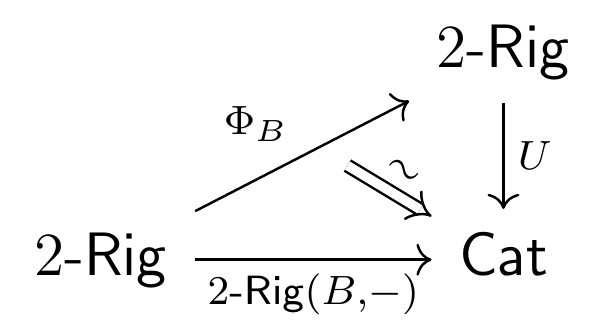
There is a 2-category of 2-birigs. Analogously with birings, for any 2-birigs $\mathsf{B}$ and $\mathsf{C}$ there is a 2-birig $B \odot C$ corresponding to endofunctor composition. This equips the 2-category $\mathbf{2Birig}$ with a monoidal structure. We define a 2-plethory to be a pseudomonoid — roughly, a monoid object up to coherent isomorphism — in $(\mathbf{2Birig}, \odot)$ . The multiplication in this pseudomonoid is called the plethysm tensor product.

Just as $\mathbb{N}[x]$ is the free rig on one generator, we prove that $\mathsf{Schur}$ is the free 2-rig on one generator. It follows that $\mathbf{2Rig}(\mathsf{Schur}, -)$ lifts to the identity 2-functor on $\mathbf{2Rig}$ :

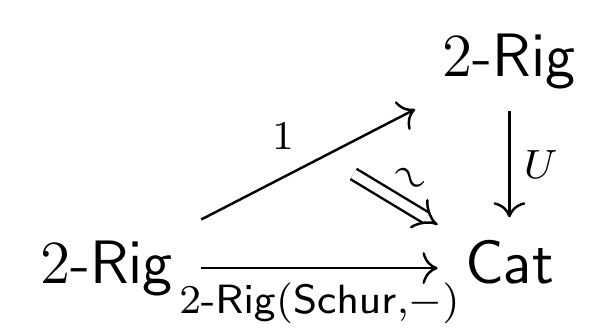
This makes $\mathsf{Schur}$ into a 2-birig, and indeed a 2-plethory. This captures the fact that we can compose Schur functors.

Taking the Grothendieck group of $\mathsf{Schur}$ , we obtain the known ring-plethory structure on $\Lambda$ , the ring of symmetric functions. The birig structure is fairly straightforward. The rig-plethory structure takes considerably more work. Most subtle of all is the biring structure, and in particular the co-negation, which involves $\mathbb{Z}_2$ -graded chain complexes of Schur functors and their Euler characteristic. This is connected to the ‘rule of signs’ in Joyal’s theory of species.

Outline of the paper

The paper is long, because there’s more to it than described above, and we try to explain everything in a gentle manner. Here’s how it goes.

Section 2 begins with an overview of the classical theory of Schur functors in representation theory, as well as their relation to finite-dimensional linear species, which we call polynomial species. The rest of this section builds up to our abstract definition of Schur functors as endomorphisms of the forgetful 2-functor $U \colon \mathbf{2Rig} \to \mathbf{Cat}$ .

Our first main result, Theorem 3.1, is that the category $\mathsf{Schur}$ of abstract Schur functors is equivalent to the category $\mathsf{Poly}$ of polynomial species. Section 3 is dedicated to proving this. En route, we prove in Theorems 3.2 and 3.2 that $\mathsf{Poly}$ is the underlying category of the free 2-rig on one generator, and that this 2-rig represents the 2-functor $U \colon \mathbf{2Rig} \to \mathbf{Cat}$ .

In Section 4 we define 2-birigs, a categorification of the notion of biring. In Theorem 4.4 we show that $\mathsf{Schur}$ has a 2-birig structure coming from its equivalence with the free 2-rig on one generator.

In Section 5, we begin by exposing an alternative perspective on birigs. Birigs and birings are examples of the more general notion of $M$ -bialgebras: that is, bialgebras of a monad $M$ on $\mathsf{Set}$ . Moreover, the category of $M$ -bialgebras admits a substitution (non-symmetric) monoidal structure. This allows us to define $M$ -plethories as monoids with respect to this monoidal structure. Then we use this perspective to categorify the notion of rig-plethory, obtaining the concept of 2-plethory. In Theorem 5.15 we give $\mathsf{Schur}$ the structure of a 2-plethory.

In Section 6 we begin the decategorification process by studying the rig of isomorphism classes of objects in $\mathsf{Schur}$ . We denote this rig by $\Lambda_+$ , and call its elements positive symmetric functions, since it is a sub-rig of the famous ring of symmetric functions, $\Lambda$ . In Theorem 6.7 we equip $\Lambda_+$ with a birig structure using the 2-birig structure on $\mathsf{Schur}$ , and in Theorem 6.12 we equip $\Lambda_+$ with a rig-plethory structure using the 2-plethory structure on $\mathsf{Schur}$ .

In Section 7 we study the group completion of $\Lambda_+$ , which is $\Lambda$ . This is evidently a ring, but making it into a biring is less straightforward: to define co-negation in this biring and prove its properties we need the homology of $\mathbb{Z}_2$ -graded chain complexes of Schur functors. Co-negation then involves a grading shift — a trick one often sees in categorification these days. We make $\Lambda$ into a biring in Theorem 7.12, and make it into a ring-plethory in Theorem 7.13.

Posted at June 2, 2021 10:15 AM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/3316

79 Comments & 1 Trackback

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Special you’re welcome! BTW this ring is also the free lambda-ring on one generator, the main theorem of Knutson’s* book “Lambda-rings and the representation theory of the symmetric group”.

*my father

Posted by: Allen Knutson on June 2, 2021 11:27 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

In the paper we acknowledge you as the “Prime Instigator”, but maybe we should have thanked your father too.

We only talk about $\lambda$ -rings a tiny bit in the paper. On page 31 we point out that a ring-plethory $B$ can be seen as a right adjoint comonad

$\Phi_B : \mathsf{Ring} \to \mathsf{Ring}$

which is the viewpoint hinted at in this blog article, or equivalently a left adjoint monad

$\Psi_B : \mathsf{Ring} \to \mathsf{Ring}$

When we take our ring-plethory to be $\Lambda$ , $\Psi_\Lambda$ maps any ring $R$ to the free $\lambda$ -ring on $R$ .

Posted by: John Baez on June 2, 2021 11:49 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

So this adjoint monad-comonad pair is arising from the adjoint triple here.

Not too far from $\mathbb{F}_1$ -territory.

Posted by: David Corfield on June 3, 2021 7:44 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Right, but it’s a bit of chicken vs. egg. Our point of view is that that adjoint triple is explicable in terms of composition of Schur functors. As soon as you have a right adjoint comonad – and here the comonad structure comes from the Schur functor composition and unit – you have an adjoint triple.

Posted by: Todd Trimble on June 3, 2021 1:51 PM | Permalink | Reply to this

GRT

$MathML-enabled post (click for more details).$

In geometric representation theory the most natural ring isn’t Symm but Symm[q,t], with two extra variables. Basically, instead of making the $n$ th graded piece using $Rep(S_n) = K([pt/S_n]) \sim H([C^{2n}/S_n])$ , one resolves that Chow variety using the Hilbert scheme and works with $H(Hilb_n(C^2))$ . At which point, why not do equivariant cohomology instead of ordinary, w.r.t. the $T^2$ that acts on the plane.

Do you see any way to naturally involve the two extra variables in these higher-categorical structures?

Posted by: Allen Knutson on June 3, 2021 5:21 AM | Permalink | Reply to this

Re: GRT

$MathML-enabled post (click for more details).$

I’ll tell you in another 14 years.

Posted by: John Baez on June 3, 2021 6:57 AM | Permalink | Reply to this

Re: GRT

$MathML-enabled post (click for more details).$

> I’ll tell you in another 14 years.

laura

Posted by: Joachim Kock on June 24, 2021 9:16 PM | Permalink | Reply to this

Re: GRT

$MathML-enabled post (click for more details).$

I feel as if I have a whole bunch of stupid questions I’d need to ask before I really understand the point of this approach, which sounds very interesting. The short answer is as John said: we haven’t thought about it.

For us, the natural starting point is the free thing on one variable, where “thing” in this case means “symmetric monoidal Cauchy-complete Vect-enriched category”. Any time you have a free thing on one variable – whatever “thing” means! some monadic situation though – you have a simple example of a plethory in a general sense.

Is Symm[q,t] a plethory?

Posted by: Todd Trimble on June 3, 2021 2:36 PM | Permalink | Reply to this

Re: GRT

$MathML-enabled post (click for more details).$

What’s going on in Nakajima’s book on the subject (“Lectures on Hilbert schemes of points on surfaces”) is something like the following. He starts with $\oplus_n H^*(Hilb_n(C^2))$ and wants to realize it as a polynomial ring $Symm$ with a generator in each degree. You might think that the way to do that is get $Symm$ to act and show that you have a free module of rank $1$ . But no, the way to do it is get the Weyl algebra to act (multiplication operators but also differentiation operators), and use some version of Stone-von Neumann uniqueness of the resulting module.

Which makes me wonder how categorifiable these differentiation operators on $Symm$ are.

As for $Symm[q,t]$ being a free object on one variable, I worry that there’ll be some dumb thing where we replace Vect-enriched by $H^*_{T^2}$ -mod-enriched, that doesn’t say why $T^2$ rather than any other dimension.

Posted by: Allen Knutson on June 4, 2021 12:32 AM | Permalink | Reply to this

Re: GRT

$MathML-enabled post (click for more details).$

This seems perhaps very suggestive. Jim Dolan and Simon Burton and I have been discussing this Stone-von Neumann type uniqueness.

As for Symm[q,t] being a free object on one variable, I worry that there’ll be some dumb thing where we replace Vect-enriched by $H^\ast_{T^2}$ -mod-enriched, that doesn’t say why $T^2$ rather than any other dimension.

This is in the neighborhood of one of my dumb questions. I feel like I need to do reading/talking with others before asking any. $S_n$ acts on any $\mathbb{C}^{k n}$ including the case $k=1$ ; dumb category theorist that I am, I don’t immediately get the move to $k=2$ .

Posted by: Todd Trimble on June 4, 2021 2:59 AM | Permalink | Reply to this

Re: GRT

$MathML-enabled post (click for more details).$

On the rep theory side the most natural object is the basic representation of an affine Lie group, i.e., the fundamental representation corresponding to the affine vertex. This is obviously an extremely special vector space; I guess a lot of its structure should be tied up in its being a vertex operator algebra.

In the case at hand the group is $GL(1,C)$ . The loop group is $GL(1,C((z))\, )$ . The affine group is the central extension of that (where the cocycle is based on “residue” somehow, pairing up $z^k$ and $z^{-k-1}$ ), a Heisenberg. The fundamental representation is the Stone-von Neumann one we were discussing.

On the geometry side we get the weight spaces of this representation by taking $H^\ast$ of (certain of) the Nakajima quiver varieties of this affine quiver. Those are built out of cotangent bundles, which is finally where the $C^2$ comes from, as $T^\ast C$ . In the case at hand the affine quiver is $A_0$ -hat, a single vertex with a self-loop. When we double (taking the cotangent bundle) we get two self-loops. The quiver representation is then a vector space with two endomorphisms $X,Y$ and a moment map condition makes them commute. At that point we’re dealing with a module over $C[X,Y]$ or essentially a point in the Hilbert scheme.

Anyway this overlong digression is (1) the quickest way I know to lead to $C^2$ rather than arbitrary $C^n$ and (2) suggests what other fine vector spaces are out there – the basic representations of affine Lie groups.

Posted by: Allen Knutson on June 4, 2021 5:37 AM | Permalink | Reply to this

Re: GRT

$MathML-enabled post (click for more details).$

The boring answer to the last question is just that it’s a plethory over $\mathbb{Z}[q, t]$ , but I think this does match the way people do plethysm in that context.

Posted by: lambda on June 4, 2021 3:20 PM | Permalink | Reply to this

Re: GRT

$MathML-enabled post (click for more details).$

Actually I think what I said here doesn’t quite make sense. If you try to use usual definition of plethysm you’ll get $\binom{q}{k}$ and $\binom{t}{k}$ factors showing up so it doesn’t actually work over $\mathbb{Z}[q, t]$ ; you need to throw in some divided powers or something.

Posted by: lambda on June 4, 2021 6:50 PM | Permalink | Reply to this

Re: GRT

$MathML-enabled post (click for more details).$

I have so many ‘dumb category theorist questions’ about what Allen is saying that I scarcely know where to begin. I think of $Hilb^n(\mathbb{C}^2)$ as something morally like a refined version of the space of multisubsets of $\mathbb{C}^2$ : bunches of points in $\mathbb{C}^2$ , which can collide, but where we keep careful track of how the points can collide. I made a bit of progress understanding this here:

The Geometric McKay Correspondence (Part 2).

but I fizzled out before I managed to use it to understand the McKay correspondence, despite a lot of help from David Speyer.

So what does this have to do with Schur functors? Well, Schur functors are secretly the same as functors from the groupoid of finite sets to $FinVect$ , which are more or less the same as vector bundles on the ‘space of finite sets’. By ‘the space of finite sets’ I mean the space of finite subsets of $\mathbb{R}^\infty$ , given a certain topology that does not allow collisions: in this topology all the $n$ -element subsets lie in a different connected component from the $m$ -elements subsets when $n \ne m$ . With this topology (which I’m not really explaining, but is not tricky), the space of finite sets is the classifying space of the groupoid of finite sets.

So it seems like I’m studying finite subsets of $\mathbb{R}^\infty$ , while Allen is talking about finite multisubsets of $\mathbb{C}^2$ , but in a way that keeps careful track of how points collide.

Is this a complete coincidence or should we really think of these things as analogous here, to understand how symmetric functions are related to the ‘enhanced’ symmetric functions Allen is talking about?

Posted by: John Baez on June 4, 2021 4:37 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Great to see this after so many years.

Back in the day I was also inspired by Hazewinkel’s enthusiasm. He wrote at around the same time

Niceness theorems

It appears that many important mathematical objects (including counterexamples) are unreasonably nice, beautiful and elegant. They tend to have (many) more (nice) properties and extra bits of structure than one would a priori expect…[p. 107]

I wrote about this in the context of free entities in Understanding the Infinite I: Niceness, Robustness, and Realism. Now we have a further understanding of his key example.

Posted by: David Corfield on June 3, 2021 7:24 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Over on Twitter, John was remarking how the “unreasonable niceness” becomes reasonable, once one understands the situation in terms of universality.

I was reminded of an old MO question I posed along these lines.

Now we have an $M$ -plethory machine to churn out examples for any monad $M$ on $Set$ , what other interesting examples are there?

I guess having a couple of interacting operations helps in the rig/ring case. The free, say, convex space on one generator isn’t terribly interesting for the distribution monad.

I couldn’t see if this story is being categorified to 2-plethories for 2-monads on $Cat$ .

Posted by: David Corfield on June 4, 2021 8:58 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Right, we thought about this too. The approach we take for M-plethories should be easy to replicate for 2-monads on Cat. The paper was getting long though, and we decided this didn’t serve the goal of seeing the 2-plethory structure on Schur descend to Lambda.

Posted by: Joe Moeller on June 4, 2021 1:49 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

The last subsection of section 5 goes very briefly into 2-plethories, but we believe the general story can be categorified for general 2-monads on Cat. One tool we use for the case of monads on Set is an adjoint lifting theorem, which involves reflexive coequalizers, and which implies as a corollary that lifts of representables

$\hom(A, -): MAlg \to \mathsf{Set}$

through the forgetful functor $U: MAlg \to \mathsf{Set}$ are the same as right adjoint endofunctors $MAlg \to MAlg$ . I think that the categorification of the adjoint lifting theorem involves codescent objects, and that the analogue of the corollary holds, but going into this would make an already long paper even longer.

One thing that was puzzling for a while: how is it that a “trivial” 2-plethory

$Id: 2\text{-}\mathsf{Rig} \to 2\text{-}\mathsf{Rig}$

given by the free 2-rig on one object gives rise to such a highly non-trivial plethory

$W: Ring \to Ring$

by decategorification? One thing we discovered is that there is a little more to “decategorification” than may first meet the eye! People may think, “what’s the problem? you’re just taking isomorphism classes of objects”, but learning how to say it right was one of the biggest problems we had to solve (section 6). In effect, one has to decategorify in stages.

I’m skeptical that 2-plethories always decategorify down to plethories.

Posted by: Todd Trimble on June 4, 2021 2:41 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

David wrote:

I couldn’t see if this story is being categorified to 2-plethories for 2-monads on Cat.

As Joe said, we decided to take a shortcut to avoid the need to develop some 2-category theory (or find it lurking in the literature).

In the case of $M$ -plethories we gave four equivalent definitions in Section 5.1. Here are three: an $M$ -plethory can be seen as a monoid in $M$ -bialgebras, but also as a left adjoint monad on the category of $M$ -algebras, or a right adjoint comonad. When categorifying we decided not to recapitulate this whole story, but only the bare minimum that we needed, so Section 5.2 starts like this:

Next we categorify the concept of rig-plethory. We believe it is possible to categorify the entire preceding story. For example, Theorem 5.4 should categorify to the statement that any lift $\Phi : \mathbf{2Rig} \to \mathbf{2Rig}$ of a representable $\mathbf{2Rig}(B, -) : \mathbf{2Rig} \to \mathbf{Cat}$ through the forgetful functor $U : \mathbf{2Rig} \to \mathbf{Cat}$ must be a right 2-adjoint. However, proving this would require a detour through some 2-categorical algebra, including for example a 2-categorical analogue of the adjoint lifting theorem [F. L Nunes, On biadjoint triangles]. Since we have a number of equivalent definitions of $M$ -plethory, we prefer to categorify the one most convenient for our purposes. So, we define a 2-plethory as a right 2-adjoint 2-comonad:

Definition. A 2-plethory is a 2-comonad $\Phi : \mathbf{2Rig} \to \mathbf{2Rig}$ whose underlying 2-functor is a right 2-adjoint.

As you can see we are also not bothering to define $M$ -2-plethories for an arbitrary 2-monad on $\mathbf{Cat}$ , but just ‘2-rig 2-plethories’. So there’s a lot of room for growth here.

As you suggest, though, the first step would be to ponder other interesting examples of $M$ -plethories in the 1-categorical context. These are usually called Tall–Wraith monoids (after the enormous ghostly warriors in Lord of the Rings), and some have been studied here:

Andrew Stacey and Sarah Whitehouse, Tall–Wraith monoids.

For some reason I’ve never looked into other examples. I guess my main interest is in the free 2-rig on one generator, as an insanely fruitful concept in representation theory, and also a tiny taste of ‘2-algebraic geometry’ (since it’s a kind of categorification of $\mathbb{Z}[x]$ , or the affine line).

Posted by: John Baez on June 4, 2021 3:00 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Thanks for all the interesting answers.

On the theme of interesting free objects on one generator, I was wondering what happens with $E_{\infty}$ -ring spectra. There’s a mention here in the talk by Saul Glasman:

The Barratt-Priddy-Quillen theorem, arguably one of the most striking in topology, states that the K-theory of the category of finite sets is equivalent to the sphere spectrum. We’ll state and prove a multiplicative analog of the theorem, giving a simple category whose K-theory can be identified with the free E-infinity ring spectrum on one generator. If time permits, we’ll discuss the combinatorics of divided power spectra and other future directions.

Slide access is indirect, but available here.

$\mathbb{S}[x]= \Sigma^{\infty} \coprod_{n\geq 0 }B \Sigma_n$ .

Posted by: David Corfield on June 5, 2021 9:31 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Part of what you mentioned amounts to this:

The groupoid $\mathsf{S}$ of finite sets is a lot like a commutative rig, since you can add and mutiply finite sets, but not subtract. In fact, $\mathsf{S}$ is a lot like the natural numbers.

There’s a way to turn $\mathsf{S}$ into a space, and then this space acts a lot like a commutative rig. If you then throw in additive inverses, you get a space that’s a lot like a commutative ring. In fact, it’s a lot like the integers. It’s the ‘sphere spectrum’. A bit more precisely, it’s the space $\Omega^\infty S^\infty$ .

It’s good to break these ideas into parts:

You can take any category and convert it into a space, by taking the ‘geometric realization of its nerve’.
If you take any symmetric monoidal category and convert it into a space, this space will be a commutative topological monoid up to coherent homotopy. In the jargon favored by homotopy theorists, it will be an ‘ $E_\infty$ space’.
If you go further and throw in additive inverses, your space will become a ‘connective spectrum’. This is nicely worked out and explained in Thomason’s 1995 paper Symmetric monoidal categories model all connective spectra.
If you take any symmetric rig category — roughly, a category with an $\otimes$ and $\oplus$ symmetric monoidal structures, with $\otimes$ distributing over $\oplus$ in a coherent way — and convert it into a space, this space will be a commutative topological rig up to coherent homotopy. This is what homotopy theorists call an ‘ $E_\infty$ ring space’.
If you then throw in additive inverses, you get a commutative topological ring up to coherent homotopy. In the jargon favored by homotopy theorists, this is called a ‘connective $E_\infty$ ring spectrum’. See the 1977 book $E_\infty$ -Ring Spaces and $E_\infty$ -Ring Spectra by Peter May and friends.

I find it simpler to work with $\mathsf{S}$ itself as long as possible: category theory feels ‘lighter’, less technical, than homotopy theory or $(\infty,1)$ -category theory. But for some constructions we need to switch from categories to spaces, or spectra.

Anyway, there should be a nice homotopy-theoretic analogue of what we did in our paper. $\mathbb{Z}[x]$ is the free commutative ring on one generator. $\mathbb{N}[x]$ is the free commutative rig on one generator. $\mathsf{Schur}$ is the free symmetric 2-rig on one generator, according to a particular hand-crafted definition of ‘2-rig’. But there should also be an interesting ‘free $E_\infinity$ -ring space on one generator’, and an interesting ‘free $E_\infty$ ring spectrum on one generator’. Does anyone here know about them?

The sphere spectrum is the free $E_\infty$ ring spectrum on no generators. That’s well known. But we should go ahead and start throwing in generators, and then relations, to get analogues of polynomial rings $\mathbb{Z}[x_1, \dots, x_n]$ and then more general commutative rings—or if you want to show off, affine schemes. This should be studied already in work on brave new algebra (which isn’t so brave or new anymore). But I haven’t gone down this road so I don’t know what’s been done!

The free $E_\infty$ ring spectrum on one generator should be a kind of ‘plethory spectrum’. Has someone studied this? Clark Barwick has some notes on plethories and the free symmetric monoidal $(\infty,1)$ -category on one generator, which come quite close to this idea.

Posted by: John Baez on June 6, 2021 9:54 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

there should also be an interesting ‘free $E_{\infty}$ -ring space on one generator’, and an interesting ‘free $E_{\infty}$ -ring spectrum on one generator’. Does anyone here know about them?

I think I was giving you the latter above:

$\mathbb{S}[x]= \Sigma^{\infty} \coprod_{n\geq 0 }B \Sigma_n.$

Posted by: David Corfield on June 7, 2021 7:25 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Oh wow, I just saw Barratt–Priddy–Quillen, sphere spectrum, and something that looked vaguely like a construction of the sphere spectrum — and didn’t notice that this was about something more interesting: the free $E^\infty$ ring spectrum on one generator! Thanks, and sorry!

So, Glasman is getting the free $E^\infty$ ring spectrum on one generator by taking a certain subcategory $\mathcal{P}$ of Joyal’s species and turning it into a spectrum.

A species is a functor

$F: \mathsf{S} \to \mathsf{Set}$

where $\mathsf{S}$ is the groupoid of finite sets. Species describe structures on finite sets — but some merely describe properties of finite sets. A key example is the species $A_n$ , which I call being an $n$ -element set.
We have $A_n(X) = 1$ if $X$ has $n$ elements and $A_n(X) = 0$ otherwise.

Glasman’s $\mathcal{P}$ is the full subcategory of species whose objects are finite coproducts of $A_n$ ’s (for varying $n$ ).

The reason it’s important is this: it’s the free symmetric monoidal category with finite coproducts on one generator (where we require the monoidal structure to distribute over coproducts). We can think of this as a rather primitive sort of 2-rig where we only have coproducts, not more general colimits.

Glasman is turning $\mathcal{P}$ into a spectrum using its additive symmetric monoidal structure, given by the coproducts.

At least this is what he seems to say.

But I’m a bit confused: since $\mathcal{P}$ has an initial object won’t its nerve be contractible? Some things Glasman writes makes me suspect he’s really getting a spectrum from the groupoid $core(\mathcal{P})$ , not $\mathcal{P}$ itself. $core(\mathcal{P})$ inherits a symmetric monoidal structure from coproducts in $\mathcal{P}$ but these are no longer coproducts in $core(\mathcal{P})$ , and $core(\mathcal{P})$ doesn’t have an initial object.

So: this talk was in 2013. What’s happened since then?

Posted by: John Baez on June 7, 2021 6:22 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

He says that the nerve of the maximal subgroupoid $iso(\mathcal{P})$ is the free $E_{\infty}$ ring space on one generator.

Posted by: David Corfield on June 7, 2021 8:23 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Okay, that’s just how I thought it should work. I hadn’t read that far into the slides; I was confused because earlier he says

What is this free ring category? It’s about as simple as it could be.

and then he creates $\mathcal{P}$ by freely adjoining finite coproducts to what I’m calling $\mathsf{S}$ . Then he takes the K-theory of $\mathcal{P}$ to get an $E^\infty$ ring spectrum.

But I guess his concept of ‘K-theory of a symmetric monoidal category’ amounts to first taking the core, then the nerve, and then group completing. Maybe that’s how everyone does it these days?

And indeed, he takes the core of $\mathcal{P}$ and then takes the nerve of that to get an $E^\infty$ ring space: the free $E^\infty$ ring space on one generator. Group completing that should then give an $E^\infty$ ring spectrum: the free $E^\infty$ ring spectrum on one generator.

Posted by: John Baez on June 7, 2021 8:40 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

From Barwick’s notes mentioned above:

The K-theory of a plethory is a plethory…

The punchline is the following: categorification takes a trivial plethory to a nontrivial plethory. This is just like redshift, which says that applying K-theory makes things more interesting!

This might be thought to be in tension with Todd’s comments on how it’s decategorification that’s surprisingly making a trivial 2-plethory into “highly non-trivial” plethory.

Is the resolution that Barwick is taking “categorification” to be what you would see as a map from plethory to 2-plethory followed by decategorification?

Posted by: David Corfield on June 8, 2021 11:50 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Well, I’m confused by this and wonder if in the punchline he meant “decategorification” instead of “categorification”. You start with the “trivial” plethory (“trivial” meaning initial) $Perf_{\mathbb{C}}[x]$ at a higher level, apply $K_0$ theory which I think of as a decategorification process, and wind up with the nontrivial plethory $\Lambda$ .

Otherwise, this works looks very interesting!

Posted by: Todd Trimble on June 8, 2021 1:35 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Todd is right, of course. I meant to say “decategorification” in the punchline. People might be interested in the work that Mathew, Nikolaus, and I did (https://arxiv.org/abs/2102.00936) on the polynomial functoriality of K-theory, which (I think) is a pleasant approach to getting this sort of operations on higher K-theory too.

(John, Joe, and Todd: your paper looks cool!)

Posted by: Clark Barwick on June 8, 2021 4:47 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

I wonder if the noncommutative symmetric functions, cf eg \S 4F of Cartier’s Primer

http://preprints.ihes.fr/2006/M/M-06-40.pdf

might be part of an interesting plethory (in some nice category of noncommutative rings, perhaps topologized or filtered?).

[This seems intimidating enough to ask first about such things over the rationals.]

Posted by: jackjohnson on June 8, 2021 9:22 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

It would be interesting to make something like this work, but there is something that looks like a barrier (to me). If I remember right, Bergman and Hausknecht in their book prove that there are basically only two kinds of operations a plethory for general rings (i.e. not necessarily commutative ones) can have, namely endomorphisms and anti-endomorphisms. This is very much unlike the case for commutative rings, where plethories can have all sorts of operations like derivations, lambda operations, and p-derivations.

This isn’t correct on the nose, because any polynomial word (noncommutative!) in any endomorphisms and anti-endomorphisms in any plethory will be another operation and it typically won’t be an endomorphism or an anti-endomorphism. That’s why I snuck in the word “basically” above. I can’t remember the exact statement of their theorem. Perhaps it’s just that a plethory for (general) rings is generated by its endomorphisms and anti-endomorphisms.

But the upshot is that there are no kinds of operations in noncommutative plethories that all your algebraist colleagues didn’t know about already. Just algebraic expressions in endomorphisms and anti-endomorphisms.

This is a bit disappointing. I’m not sure I’m ready to close the book on noncommutativity and plethories, but for now I don’t know of any promising directions.

It’s a bit like the jump from groups to modules. Groups (and monoids) are born to act on things. While they can be acted on by other things, namely other groups and monoids, they are primarily subjects of actions instead of objects. Givers instead of receivers. While they can be acted on by monoids, that’s pretty much it. Kan’s theorem says that plethories for groups are generated by endomorphisms. So the most general object that knows how to act on a group is just a monoid, and they can act on anything in any category. Boring! :)

But if we restrict ourselves to commutative groups, then it flips. The hunter becomes the hunted, or something. We think of abelian groups primarily as objects of actions instead of the subjects. Abelian groups can be thought of as groups or as modules (Z-modules), but to me they feel more like modules. Abelian-group theorists seem more like module theorists than group theorists. Sure enough, plethories for abelian groups– in other words, rings– are much richer than plethories for general groups.

Similarly with rings. The purpose of general rings is to act on abelian groups. They are plethories for abelian groups. Plethories for rings are not so interesting, the question of what knows how to act on a general ring is not such an interesting one. But if we impose commutativity on our rings, then there is the possibility of them being acted upon by much richer objects, namely the (original) plethories for commutative rings. We get lambda-rings, delta-rings, differential rings, and all sorts of rich structure.

This picture always reminds me of the aphorism that everyone is a child until they become a parent. Your purpose is to act until you can be acted upon, at which point that becomes what you do.

Posted by: James Borger on June 11, 2021 12:21 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Very interesting! Could there be something Eckmann-Hilton-like going on here, where the commutative object is more easily acted on since it arises from a monoid or group object internal to a certain kind of category?

Posted by: David Corfield on June 11, 2021 3:05 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

That’s an interesting thought. Alas, I’m sure I don’t know what to make of it…

But I am sure that there’s a rich, rich overlap between the higher-categorical world and the biring/plethory world. Just to mention one data point, in Drinfeld’s recent paper “Prismatization”, he explains how ring stacks give rise to cohomology theories. He’s particularly interested in prismatic cohomology, but crystalline, de Rham, Dolbeault are super fun baby cases. A ring stack is, sort of by definition, just Spec of a derived biring which is concentrated in two degrees. So “slightly categorified birings” = de-Rham-like cohomology theories.

Posted by: James Borger on June 15, 2021 12:19 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Presumably there’s something higher-categorical going on in this observation from nLab: Lambda-ring:

the Grothendieck group of a monoidal abelian category is always a ring, called a Grothendieck ring. If we start with a braided monoidal abelian category, this ring is commutative. But if we start with a symmetric monoidal abelian category, we get a $\lambda$ -ring,

working its way down column $n =1$ of (an abelian version of) John’s periodic table, so deloopable to 2-, 3-, 4-categories.

Posted by: David Corfield on June 16, 2021 7:38 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

I’m the one who wrote that observation on the nLab. I found it very striking, when I first noticed it, how the Grothendieck group gets some extra structure in the symmetric case, over and beyond the obvious structure coming from the braided case. It would be fun to examine how these generalizes to other columns in the periodic table.

Posted by: John Baez on June 16, 2021 10:25 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

That’s great! Is it easy to say what the reason is?

Posted by: James Borger on June 16, 2021 11:12 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

I was having a look around for this claim. Some notes, Remark 3.1.24 simply claim it.

I found a talk by Andreas Holmstrom that claims the Grothendieck ring of a Tannakian category is a lambda-ring (slide 6). (Tannakian symbols there look interesting.)

Posted by: David Corfield on June 18, 2021 7:57 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Reaching back to the early days of the blog, we were hearing lots from you on providing a

‘purely combinatorial’ substitute for the theory of representations of $G$ on vector spaces.

This in response to

But of the millions of other categories in the night sky, why is the category of finite-dimensional vector spaces the one whose objects it is so useful to make finite groups act on?

This latest work of yours deals with representations on finite-dimensional vector spaces. Does the groupoidification program have anything to say to this?

Posted by: David Corfield on June 3, 2021 7:37 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Yes, this should combine with groupoidification in an interesting way. Very roughly our paper is a study of the free 2-rig on one generator, but it relies on a specific hand-crafted definition of ‘2-rig’ suitable for our purposes — and this definition has vector spaces over a chosen field of characteristic zero built in, giving our notion of linearity at the morphism level of the 2-rig. We could try swapping out the vector spaces for something else, as we do in groupoidification. We might go one step up the $n$ -categorical ladder in the process.

I’m talking about the decisions here:

A linear category is an essentially small category enriched over $\mathsf{Vect}$ , the category of vector spaces over a field $k$ .
A linear category is Cauchy complete when it has biproducts and all idempotents split.
A symmetric monoidal linear category is a linear category with a symmetric monoidal structure for which the tensor product is bilinear on hom-spaces.
A 2-rig is a symmetric monoidal linear category that is also Cauchy complete.

A 2-rig should have a kind of linear structure at the object level, given for example by colimits, but also some linear structure at the morphism level. Here we chose linearity at the morphism level to be described by vector spaces over a field $k$ of characteristic zero. So, our 2-rigs are $Vect$ -enriched. Then we chose the bare minimum amount of enriched colimits, namely the absolute colimits. Both these decisions are adjustable, and it’s very interesting to try different versions.

Right now I’m most interested in going from vector spaces over a field of characteristic zero to vector spaces over an arbitrary field — or even better, working over $\mathbb{Z}$ ! But these are fairly timid moves compared to what you’re suggesting.

A lot of modern math is in quest of a “deeper base”, trying to sink beneath fields and even the integers to some deeper concept of linearity — and still do interesting mathematics. Groupoidification is one approach.

Posted by: John Baez on June 4, 2021 3:13 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

The characteristic zero assumption is already quite strong, because it allows you to do symmetrisation by dividing by n!. Even modular representations should pose significant technical hurdles. But yes, the whole structure is screaming

“what changes (obstructions do you have) when you replace finite dimensional vectorspaces by finitely generated modules over a Noetherian Ring”?

One hint is that $H^*BU = Z[[c_1, c_2, c_3, .....]]$ . Here BU is considered as the classifying space of vector bundles and the graded ring generated by the Chernclasses is the symmetric functions in the “Chern roots” the first Chernclasses of the canonical line bundles on the infinite maximal flagvariety.

Posted by: Rogier Brussee on June 7, 2021 12:51 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

People talk of divided power structures in the context of non-zero characteristic.

Sounds intriguing here:

this appearance of divided powers in characteristic $p$ is sort of pathological, and we’d like to resolve this. A philosophy that’s been becoming more prevalent recently is that the existence of divided powers is because one’s working with HZ as the base; if one instead regards the sphere spectrum as one’s base, then the divided power pathology vanishes.

Posted by: David Corfield on June 7, 2021 1:32 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Thanks for this very helpful reference to a very interesting blog. Lars Hesselholt strongly advocates this point of view, cf the discussion of B"okstedt periodicity at

https://www.routledgehandbooks.com/doi/10.1201/9781351251624-15

Posted by: jackjohnson on June 7, 2021 4:31 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Right now I’m most interested in going from vector spaces over a field of characteristic zero to vector spaces over an arbitrary field…

Maybe of interest. In the final section of his paper – Classification of plethories in characteristic zero, Magnus Carlson writes

In this section we will start a classification for plethories over a perfect field $k$ of characteristic $p$ .

Posted by: David Corfield on June 10, 2021 8:01 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Thanks! And I should try to understand this result of his:

All plethories over characteristic zero fields are linear, in the sense that they are free plethories on a bialgebra.

Posted by: John Baez on June 10, 2021 9:53 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

This

MR1348573 Hunton, John; Ray, Nigel, A rational approach to Hopf rings. J. Pure Appl. Algebra 101 (1995), no. 3, 313 – 333

might be relevant.

Posted by: jackjohnson on June 11, 2021 12:33 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

“Right now I’m most interested in going from vector spaces over a field of characteristic zero to vector spaces over an arbitrary field…”

One thing interesting about polynomial functors in char p>0 is that the p-th Adams operation becomes effective. In characteristic 0, the Adams operations on K-theory do not come from functors. They are only virtual classes, unlike the lambda-operations which do come from functors, namely the exterior powers. Another way of saying it is that power sum symmetric functions are not Schur positive. They are not effective classes in the Grothendieck ring of the polynomial functors.

But with polynomial functors in char p, the p-th Adams operation is effective. It’s just the Frobenius map. Presumably in this case, the effective polynomial functors also form a rig-plethory, and for “general reasons”. (This was Question 3 here.)

There is probably lots of fun to be had here. For instance: Is the rig of effective classes generated by the p-th Adams/Frobenius operation together with the usual Schur functors?

Posted by: James Borger on June 11, 2021 12:46 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

James wrote:

In characteristic 0, the Adams operations on K-theory do not come from functors. They are only virtual classes, unlike the lambda-operations which do come from functors, namely the exterior powers. Another way of saying it is that power sum symmetric functions are not Schur positive.

Right. One reason I got interested in this 2-plethory stuff was because I was trying to understand your proposal to think about the ‘field with one element’ using λ-rings. You had told us about the orthodox and heterodox approaches to λ-rings. I already knew (or guessed) that we could understand the orthodox approach very nicely by categorifying it, using the category of Schur functors. So I wanted to see if the Adams operations, so fundamental in the heterodox approach, could be seen as Schur functors. I asked on MathOverflow and got a negative answer:

When and why are Adams operations “non-negative”?, November 3, 2019.

But I foolishly didn’t look more deeply into the characteristic $p$ situation… or read your papers. So, I decided to march ahead anyway with the more limited goal of understanding the category of Schur functors as a 2-plethory. But now you’re rekindling my original hopes.

But with polynomial functors in char $p$ , the $p$ -th Adams operation is effective. It’s just the Frobenius map. Presumably in this case, the effective polynomial functors also form a rig-plethory, and for “general reasons”. This was Question 3 here.)

Great!

I’m really hoping that we can get a nice 2-plethory that includes both Adams operations, viewed as polynomial functors of some sort, and also Schur functors. My dream is that something like this will shed light on the field with one element.

Posted by: John Baez on June 11, 2021 9:23 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

If you’re willing to decategorify for a moment, there is a perfectly good rig-plethory containing all the Adams operations and all the Schur operations. It is the rig of ‘monomial positive’ symmetric functions, which one might denote $\Lambda_{\mathbb{N}}$ . These are the symmetric functions in variables $x_1,x_2,\dots$ , for which all monomials have coefficients $\geq 0$ . You might have been aware of this rig-plethory already.

But you asked about 2-plethories, so we might try to categorify this example. I don’t know an answer, but here is a thought. You can say that Schur positivity is to monomial positivity as representations of $GL_n$ are to $S_n$ -invariant representations of the diagonal torus $(\mathbb{C}^*)^n$ . Now Schur positivity is all about functors from vectors spaces to vector spaces, such as the exterior power functors. So to get an analogue for monomial positivity, you might try replacing vector spaces in the Schur set up with some kind of ‘axial vector spaces’. By this I mean something like a vector space together with an unordered choice of coordinate axes. Going with this definition, then for vector bundles, an axial structure would be a decomposition as an unordered sum of line bundles. Then the Adams operation $\psi_n$ would send an axial vector bundle to the sum of the $n$ -th tensor powers of its ‘axes’, by which I mean these line bundles.

This all looks pretty close to the ‘splitting principle’ from the theory of lambda-rings and K-theory. So maybe there’s something to it.

Posted by: James Borger on June 12, 2021 12:48 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Actually, for vector bundles an axial structure should probably be a local property. So it might be a decomposition into unordered sets of line bundles over a chart, together with isomorphisms between them on the overlaps which satisfy a cocycle condition on the triple overlaps. So as you go around a big loop, the axes in the fiber over a given point could get permuted. These things probably have an old name that everyone knows, possibly including myself!

Posted by: James Borger on June 12, 2021 1:10 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

FWIW quasisymmetric functions define analogs of Chern classes for vector bundles provided with a decomposition as an ordered sum of line bundles.

Posted by: jackjohnson on June 12, 2021 1:24 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Hmm. Thanks, Jack. Can you point me to a place where this is explained?

So perhaps the mystery of why QSym does not seem to want to be a plethory is that it’s really a Chern/homological thing rather than a lambda/K-theoretic thing.

If I had a better sense of what I mean, I could explain it better, but what I have in mind is that the plethory $\Lambda$ represents the big Witt vector functor $R\mapsto W(R)$ , with all its structure. There is a similar functor, the Chern ring functor $R\mapsto Ch(R)$ , where $R$ is now a lambda-ring if I remember (and $Ch(R)$ is nonunital, which can be ‘repaired’ in the usual way if you like). In Riemann-Roch business, $Ch(R)$ is meant to be the universal receptacle for a theory of Chern classes from the lambda-ring $R$ . The two constructions $Ch(R)$ and $W(R)$ are the same as abelian groups– both being $1+t R[[t]]$ – so as set-valued (or abelian-group-valued) functors they are represented by the same object, namely the ring $\Lambda$ of symmetric functions. But their multiplication laws are different. (See here.) Another sign that they really are different things is that $W$ inputs rings and outputs rings, making it potentially (and actually) representable by a plethory. But $Ch$ inputs lambda-rings and outputs ordinary (non-unital) rings, which are different kinds of objects. So unless and until that can be improved, it would only be represented by a (‘non-co-unital’) $\Lambda$ - $\mathbb{Z}[e]$ -biring.

The point I’m trying to make is that the ring of symmetric functions has two different co-multiplication laws that come up in this business, the ‘lambda-ring one’ and the ‘Chern one’. I think they should really be viewed as completely different objects, which just happen to have isomorphic underlying rings. But if you don’t pay attention to all their structure, specifically the co-multiplication laws, it’s easy to think of them as the same thing. (Perhaps this is like the distinction between a unipotent Lie group and a unipotent Lie algebra, which are different objects but which are also related by an exponential construction, similar to the Chern character.)

So perhaps QSym is properly thought of as being analogous to the ring representing the Chern functor rather than the ring $\Lambda$ representing the Witt functor.

Posted by: James Borger on June 13, 2021 12:57 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

I wasn’t aware of the Chern ring literature but I recall that Graeme Segal once asked if the total Chern class

(1)

\tilde{K}(X) \to \tilde{H}^0(X,\mathbb{Z}[t])^\times

(deg t = 2) is induced by a map of infinite loopspaces, which was shown not to be the case by

MR0433446 V Snaith, The total Chern and Stiefel-Whitney classes are not infinite loop maps, Illinois J. Math. 21 (1977) 300–304.

Baker and Richter, working in homotopy theory, start from the maximal torus map

(2)

\coprod B\mathbb {T}^n \to \coprod BU(n)

and its close relative

(3)

\Omega \Sigma B\mathbb{T} \to \mathbb{Z} \times B\mathbb{U}

which, from the algebraic point of view, is related to the functor sending a module to the free cotensor Hopf algebra it generates, perhaps related to the literature around

C Brouder, W Schmitt, Renormalization as a functor on bialgebras, J Pure Appl. Algebra 209 (2007) 477 - 495, https://arxiv.org/abs/hep-th/0210097 .

Commensurability of algebraic versus homotopy-theoretic approaches to noncommutativity looks like an interesting developing topic. BTW could your Frobenius flow be related to the flow Connes defined for type III von Neumann algebras (asking for a friend)?

$( \; \; : + \: \{ ) \}$

Posted by: jackjohnson on June 13, 2021 3:54 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Wow — thanks, James and Jack! This is the first time I’ve gotten a good understanding of $\Lambda_{\mathbb{N}}$ , and also the first time I’ve gotten any clue about what quasisymmetric functions are all about.

You’re making them sound like they’re very related. It’s sounding like $\Lambda_{\mathbb{N}}$ comes from studying characteristic classes of vector bundles equipped with an “axial structure” — a splitting into a sum of line bundles — while quasisymmetric functions come from studying characteristic classes of vector bundles equipped with a splitting into an ordered sum of line bundles.

Is that right? If so, this should give a homomorphism from quasisymmetric functions onto $\Lambda_{\mathbb{N}}$ .

James wrote:

Actually, for vector bundles an axial structure should probably be a local property. So it might be a decomposition into unordered sets of line bundles over a chart, together with isomorphisms between them on the overlaps which satisfy a cocycle condition on the triple overlaps. So as you go around a big loop, the axes in the fiber over a given point could get permuted. These things probably have an old name that everyone knows, possibly including myself!

It seems that an axial structure is just a way of reducing the structure group of an $n$ -dimensional vector bundle from $GL(n)$ to $S_n$ . Is that right? This seems very “field-with-one-element-ish”.

Given an $n$ -sheeted covering of a space, we can promote it to a vector bundle with axial structure using the functor that sends any $n$ -element set to the free vector space on that set.

This leads me to my third question:

Are “characteristic classes for vector bundles with axial structure” just the same as “characteristic classes for finite covering spaces”?

Posted by: John Baez on June 12, 2021 6:34 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

I should be careful: there are tricky issues because we’re talking about `stable’ vector bundles, and also because of Pontryagin-Thom, cobordism is about normal bundles rather than tangent bundles, so there are pitfulls, cf the review of

MR0678521 R Arthan, S Bullett, The homology of MO(1)∧∞ and MU(1)∧∞. J. Pure Appl. Algebra 26 (1982) 229–234

But I think this

MR2484353 A Baker, B Richter, Quasisymmetric functions from a topological point of view, Math. Scand. 103 (2008)208–242

paper works things out very elegantly. Another interesting issue is that the Hopf algebra of symmetric functions is self-dual (under the Hall product, cf MacDonald’s book, which AFAIK has no sensible topological interpretation), whereas the (commutative) Hopf algebra of quasisymm fns is dual to the noncomm alg of noncomm symm fns (essentially just the free graded associative algebra on even-degree generators). So the symm fns are nicely embedded in QSymm; but the dual of that embedding identifies the symm fns with the abelianization of NSymm.

These dualities (among other things) confuse me about relations with Gln and Sn so I had better keep my mouth shut about that. It is maybe worth mentioning tho that there are deep relations between QSymm and `multizeta values’ in number theory, cf eg

MR1467164 M E Hoffman, The algebra of multiple harmonic series, J. Algebra 194 (1997) 477–495

or Cartier’s Primer cited previously in this thread.

Posted by: jackjohnson on June 12, 2021 11:55 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

John wrote, “It seems that an axial structure is just a way of reducing the structure group of an 𝑛-dimensional vector bundle from GL(𝑛) to 𝑆𝑛. Is that right? This seems very “field-with-one-element-ish”.”

Ah, right. But what I meant was a reduction of the structure group from $GL_n$ to $N(T)$ , where $N(T)$ is the semi-direct product of $S_n$ and the torus $T=(\mathbb{C}^*)^n$ . So $N(T)$ is the normalizer of the torus $T$ .

But this is also very field-with-one-element-y! Maybe even more so! If I remember correctly, in my old F1 paper, $N(T)$ is the gadget that plays the role of $GL_n$ over $\mathbb{F}_1$ . It’s the automorphism object of affine space $\mathbb{A}^n$ together with its usual scalar action of $\mathbb{G}_{\mathrm{m}}$ . This is all in the category of $\Lambda$ -schemes, which is my stand in for descent data to $\mathbb{F}_1$ . So all rings and schemes in sight have lambda-structures—in this example in the usual way. (Ignoring the lambda-structures, it would just give usual $GL_n$ , which is why I could argue it’s ‘ $GL_{n}$ over $\mathbb{F}_1$ ’, even though it’s not a lambda-structure on the usual $\GL_n$ .)

Anyway, do we have a candidate answer then? The 2-plethory of ‘monomial functors’ would be the category of some kind of polynomial functors from the category of axial vector spaces to itself? Axial vector spaces appear to pretty obviously have direct sum and tensor product operations. Doing them pre- and post-composition would give the biring structure, and composition of them would give the plethory structure.

Posted by: James Borger on June 13, 2021 1:44 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

I think this

But what I meant was a reduction of the structure group from $GL_n(\mathbb{C})$ to $N(\mathbb{T})$ , where $N(\mathbb{T})$ is the semi-direct product of $S_n$ and the torus $\mathbb{T} = (\mathbb{C}^*)^n$ . So $N(\mathbb{T})$ is the normalizer of the torus $\mathbb{T}$ .

follows (after group completion) from the Becker-Gottlieb proof

MR0377873 The transfer map and fiber bundles. Topology 14 (1975) 1 – 12

of the Adams conjecture.

Posted by: jackjohnson on June 13, 2021 6:13 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Wait, what follows? I was just proposing a definition!

Or did you mean that the effective classes in the Grothendieck ring of ‘suitably polynomial’ endofunctors of the category of axial vector spaces agrees with $\Lambda_{\mathbb{N}}$ ?

Posted by: James Borger on June 15, 2021 1:27 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Since it’s come up, I can’t resist putting in a good word for the monomial side of the story. You might think that it’s kids’ stuff and that the Schur side of the story is for the grown ups’ table. $N(T)$ versus $GL_n$ , the monomial basis of symmetric functions versus the Schur basis, axial vector bundles versus actual vector bundles, and so on.

But here is one property of the rig-plethory $\Lambda_{\mathbb{N}}$ of monomial-positive symmetric functors has that the rig-plethory $\Lambda_+$ of Schur-positive symmetric functions doesn’t have. Call the functors (on rigs) they represent $W$ and $W_{\mathrm{Sch}}$ . So if $R$ is a ring, then $W(R)$ and $W_{\mathrm{Sch}}(R)$ agree with the usual big Witt vectors of $R$ . But for general rigs, they’re different, by Yoneda’s lemma.

Now consider $\mathbb{R}_+$ , the rig of reals $\geq 0$ . Then $W(\mathbb{R}_+)$ (but not $W_{\mathrm{Sch}}(\mathbb{R}_+)$ !) has the property that the Adams operations $\psi_n$ for integers $n\gt 1$ interpolate to define Adams operations $\psi_t$ for all real $t\gt 1$ ! The Adams operators are more commonly called the Frobenius operators $F_n$ when we’re talking about Witt vectors. So on the ‘lambda-rig’ $W(\mathbb{R}_+)$ , the Frobenius operators interpolate to a flow! Now in my old $\mathbb{F}_1$ framework (or rather the rig analogue of it), ‘ $\mathbb{R}_+$ viewed as an $\mathbb{F}_1$ -algebra’ is defined to be $W(\mathbb{R}_+)$ with its lambda-structure. So $\mathbb{R}_+$ , which has no nontrivial endomorphisms as a $\mathbb{N}$ -algebra (i.e. as a rig), acquires a flow of endomorphisms when viewed as an $\mathbb{F}_1$ -algebra. At integer values, they agree with the usual Frobenius/Adams operations which exist for all $\mathbb{F}_1$ -algebras (i.e. lambda-rings).

This fact about interpolation is not a formal one (whatever that means). You need the Edrei-Thoma theorem in the theory of total positivity. (Well, it’s certainly sufficient, and I’m not sure how to do it otherwise. But I am a bit rusty on this stuff.)

When I first discovered this picture, I thought I’d found the key to the universe. It even satisfies many of the conditions of Deninger’s spaces in his conjecture framework for analytic number theory. But I’ve never been able to do anything non-formal with it.

Posted by: James Borger on June 13, 2021 2:39 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

In case it’s of interest, in the thesis, Unstable Cohomology Operations: Computational Aspects of Plethories, I mentioned below, in 1.3.7 Adams operations are treated as ‘superprimitive elements’, while in the section from p. 151, we’re told that Adams operations may only generate a proper sub-plethory of the plethory of $\lambda$ -operations.

Posted by: David Corfield on June 12, 2021 10:04 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Yes! They definitely generate a proper sub-plethory. This is exactly the phenomenon I mentioned in another comment I just posted about adjoining suitable denominators in step 4 of the way you build up a plethory.

Posted by: James Borger on June 15, 2021 1:31 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

I imagine Joachim Kock would be a good person to have around here with his homotopy linear algebra, interest in ‘objecive combinatorics’, and his student, Alex Cebrian working on plethysm.

Posted by: David Corfield on June 7, 2021 10:44 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Here is a very short summary and advertisement of Alex Cebrian’s thesis work.

Alex’s starting point (well, from now on I will call him Cebrian, for better branding) was the incidence-bialgebra approach to ordinary substitution of power series, which is very fruitful, leading to the whole Faàdi Bruno business, as employed in quantum field theory, numerical analysis, multi-zetas, and so on. The Faàdi bruno bialgebra is the free commutative algebra on the linear forms on the vector space of power series, and its comultiplication is dual to substitution of power series. This coalgebra side of duality is somehow much more combinatorial…

Doubilet had realised the FdB as an incidence bialgebra of the lattice of partitions, but this construction requires quotienting by a certain ‘type equivalence’. Joyal, in the final section of his species paper (a section which does not actually concern species!), noticed that the Faàdi Bruno bialgebra is directly the incidence bialgebra of the fat nerve of the category of surjections (in a modern reformulation of his observation). ‘Fat nerve’ means that instead of just considering sets of strings of composable surjections, it’s about groupoids of strings of composable surjections, and now the groupoid formalism takes care of symmetry factors automatically. Joyal’s construction is really about homotopy pullbacks and homotopy fibres, although he did not formulate it like that at that time (1981). The construction becomes a special case of the incidence bialgebra construction of monoidal decomposition spaces. I’ll say a bit more about that further on.

So what is the analogous construction for plethystic substitution? The plethysm here is the notion of Pólya (like in the theory of species), not the one of Littlewood (like for representations of the general linear groups) (although of course they are closely related, as also explained in Cebrian’s thesis).

Maybe I should say something about Pólya’s notion of plethysm (1937), since the notion of plethory derives rather from Littlewood’s notion (1943). Pólya’s plethysm a substitution law for power series in countably many variables $x_1,x_2,x_3,\ldots$ . The substitution law is given by $(g \odot f ) (x_1,x_2,x_3,\ldots) := g(f_1,f_2,f_3,...)$ where $f_k(x_1,x_2,x_3,\ldots) := f(x_k,x_{2k},x_{3k},\ldots).$ Shifting the variables like that is called Vershiebung, since Pólya. Although it is an explicit operation, it may appear quite mysterious. Pólya introduced plethysm in connection with un-labelled enumeration (of groups, graphs, and chemical compounds). His theory is subsumed in the theory of species as follows. The notion of species, functors $F: \mathbb{B} \to \mathbf{Set}$ from the groupoid of finite sets to the category of sets, have associated an exponential generating series (also denoted) $F(z)$ (whose coefficents count $F$ -structures) and an ordinary generating series called the type generating series $\widetilde{F}(z)$ (whose coefficients count isoclasses of $F$ -structures (this is called unlabelled enumeration, although the terminology is not very good). The operation of substitution of species $G\circ F$ corresponds precisely to substitution of exponential generating series: $\circ$ for species corresponds precisely to $\circ$ for generating series. This is not the case for the type generating series: $\widetilde{G} \circ \widetilde{F} \neq \widetilde{G \circ F}$ . This makes it more difficult to use species for unlabelled enumeration. However, Pólya and Joyal get around it with the following mind-boggling idea: there is instead the cycle index series of a species. It is a series in countably many variable $Z_F(z_1,z_2,z_3,\ldots) := \sum_n \frac{1}{n!} \sum_{\sigma\in\mathfrak{S}_n} |\operatorname{Fix}(F[\sigma])| z_1^{\sigma_1} z_2^{\sigma_2} \cdots$ where $\operatorname{Fix}(F[\sigma])$ is the set of fixpoints for $F$ applied to the permutation $\sigma$ , and $\sigma_k$ is the number of $k$ -cycles in $\sigma$ . The point of this is that $Z_{G\circ F} = Z_G \odot Z_F$ –that’s plethystic substitution! And the second point is that both the exponential and the type generating series can be extracted from $Z$ : $Z_F(z,0,0,\ldots) = F(z) \qquad \text{ and } \qquad F(z,z^2,z^3,\ldots) = \widetilde{F}(z)$ So from this viewpoint, the upshot of plethystic substitution is that it interpolates betwen exponential and type generating series of species, in a way that allows to calculate type generating series of substitution products of species.

(It is quite a mouthful. I cannot say I have fully grasped this. If anyone can explain it in a straightforward way, I look forward to hear about it.)

Cebrian found a nice relationship between the FdB, incidence bialgebras and plethysm, showing that there is a symmetric monoidal simplicial groupoid TS whose incidence bialgebra is dual to plethystic substitution (https://arxiv.org/abs/1804.09462). Furthermore, this simplicial groupoid is quite nice: it is obtained from the fat nerve of surjections S by a certain construction T which is reminiscent of Quillen’s Q construction and Waldhausen’s S construction. Its 2-simplices are certain configurations of triangle diagrams of surjections. They are precisely the so-called transversals of Nava and Rota (1985), who had given the first combinatorial construction of plethystic substitution, through a long and intricate construction. (Joyal’s theory can also be seen as a combinatorial interpretation, but only for series that arise as cycle-index series of species, which is some specific one-variable data.)

The second part of Cebrian’s thesis (https://arxiv.org/abs/2008.09798) starts from the observation that just as S is actually the two-sided bar construction of the terminal operad, also TS is actually the two-sided bar construction of a certain operad. Then he found a general construction for operads, which when given the terminal operad as input produces the operad whose two-sided bar construction is TS. This construction too is called T. When the operad is just a monoid (considered as a one-colour operad with only unary operations), then the T-construction reduces to a construction introduced earlier by Giraudo, which by coincidence was also called T.

The T-construction for operads is not so difficult to make pictures of, but a bit involved to describe in words. For P an operad, the operations of TP are finite lists of operations in P, and the arity of such a list is its length. To substitute a list of such lists into a list it is necessary to duplicate operations in a certain way. This duplication is actually a combinatorial abstraction of the Verschiebung operator in plethysm. Altogether the operadic T-construction can be seen as a general theory for how plethystic substitution arises from ordinary substitution. It leads to many new exotic forms of plethysm, the classical being the one coming from the terminal operad. Some of these exotic plethysms had already been studied in combinatorics (Nava, Méndez, Giraudo), but now there is a general theory for them.

Posted by: Joachim Kock on June 24, 2021 10:17 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

I also wanted briefly to update on categorified Hopf algebras of symmetric functions. Not nearly as fancy as plethories or 2-plethories, but difficult enough for us – that’s Imma Gálvez, Andy Tonks and myself. Our hypothesis is that Sym (as well as QSym, NSym, FQSym, WQSym, and so on) should all be incidence bialgebras of monoidal decomposition spaces.

30-seconds intro to monoidal decomposition spaces: the incidence-coalgebra construction on a poset is simple enough. As a vector space, it is spanned by the intervals of the poset. The comultiplciation is given by $\Delta([x,y]) = \sum_{m\in [x,y]} [x,m] \otimes [m,y]$ splitting intervals in all ways. It can be described simplicially in terms of the nerve $X$ of the poset: for $f\in X_1$ we have $\Delta(f) = \sum_{\sigma \in X_2 \mid d_1\sigma=f} d_2\sigma \otimes d_0\sigma .$ It then generalises to certain categories (Leroux 1975), and in fact it turns out to generalise to certain simplicial \infty-groupoids which we call decomposition spaces [https://arxiv.org/abs/1512.07573]. They are the same thing as the 2-Segal spaces of Dyckerhoff and Kapranov, although the definition, motivation and development is quite orthogonal. Decomposition spaces are more general than Segal spaces (category objects): in a precise sense, decomposition spaces encode decomposition of objects where Segal spaces encode composition of objects.

The theory is inherently objective, in the sense that it gives coalgebras in the \infty-category LIN of \infty-groupoid slices, which is a fully homotopical version of Baez-Hoffnung-Walker groupoidification. The point of this generalisation is that virtually all combinatorial co- and bialgebras arise in this way. But this depends on what is meant by combinatorial. It is required that the structure constants are nonnegative! In particular, the notion depends on choice of basis.

Indeed, it turns out that the various classical bases for the ring of symmetric functions do not come from isomorphic decomposition spaces! In fact already over the natural numbers, all these bases are different objects, as already noted by James further up this thread.

(Fine print: it turns out monoidal decomposition spaces are not enough. A monoidal decomposition spaces is a special case of bisimplicial objects which are decomposition spaces in each direction, and which satisfies the so-called Penney condition (a beautiful categorified bialgebra-axiom condition identified by Mark Penney in his 2017 Oxford PhD thesis). Both the decomposition space condition and the Penney conditions are pullback conditions, and in the end the whole theory ends up being about calculating pullbacks. to really capture all the bases of symmetric functions, it is required to work with bisimplicial groupoids with Penney condition, rather than just symmetric monoidal decomposition spaces. For simplicity, I continue talking only about those.)

So for each of the classical bases of Sym (monomial, power-sum, complete, elementary, ‘forgotten basis’) there is a decomposition space.

In general, the simplicial maps between decomposition spaces that induce coalgebra homomorphisms are CULF maps (forward) and IKEO maps (backwards). Altogether, the relevant maps are spans of simplicial maps whose backward leg is IKEO and whose forward leg is CULF. CULF stands for conservative and unique-lifting-of-factorisations, and they are classical notions in category theory. IKEO stands for inner Kan and equivalence on objects. For categories, inner Kan is automatic, and IKEO then boils down to bijective on objects, also a very classical class of functors. Surprisingly, in the simplicial setting of decomposition spaces, both the CULF condition and the IKEO condition are conditions stating that certain squares are pullbacks!

So the base changes, which are the bread and butter of the combinatorial theory of Hopf algebras of symmetric functions, take the form of certain spans of decomposition spaces. But as one may expect, they only work in one direction, because as is well known, these change of bases most often have nonnegative integer coefficients in one direction but signs in the other direction. The decomposition spaces for the elementary, power-sum, complete, and forgotten basis symmetric functions admit a IKEO-CULF map to the monomial-basis decomposition space, but not the other way. The base changes going the other way requires minus signs which are described by Möbius inversion. (It is not too bad – in fact decomposition spaces were designed for the purpose of Möbius inversion, and the Möbius inversion principle holds universally at this level of abstraction.)

All five Sym decomposition spaces have in degree 1 the groupoid of surjections. (From the objective viewpoint, that’s the natural way of talking about partitions, but curiously, it gives different normalisations, which are more natural in terms of symmetry factors. For example, in the classical theory one would describe $h_2$ as $x_1 x_2 + x_1^2 + x_2^2$ , but in the objective setting of decomposition spaces, a more natural normalisation is $x_1 x_2 + x_1^2/2! + x_2^2/2!$ .) The distinction between the bases happens in higher simplicial degrees. The span $E \leftarrow W \to M$ defining the base change expressing elementary symmetric functions in terms of the monomial basis is given in degree 1 by taking $W$ to be the groupoid of spans of surjections $m \leftarrow r \to n$ for which $r \to m \times n$ is injective (this is to say that $r$ is an effective relation), and the projection return the two surjections. It is not so much worse in higher simplicial degree. I know I have not given enough details here to actually explain anything, but at least it gives an impression of the flavour. It has been really funny to work out. It is completely combinatorial, and it is never necessary to write out the actual ‘functions’ or their infinitely many variables. For this reason we like to think of the whole theory as a combinatorial theory of symmetric functions. And because of the new symmetry factors which are natural from a groupoid point of view, we also play with the idea that it could be called a symmetric theory of symmetric functions.

Unfortunately, it has been bugging us for several years now that we cannot figure out how to do the Schur basis :-( It seems to us that it is not combinatorial in the same way as the other five bases are. The remarks of James further up the thread are very interesting, and there is a lot to think about.

We will definitely study the Baez-Moeller-Trimble paper, hoping that it will give us a hint!

Posted by: Joachim Kock on June 24, 2021 10:41 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Likely related: the ring $\Lambda$ is also the Grothendieck group of the category of bounded-degree polynomial functors over the integers (n.b. I don’t think this is the same notion of polynomial functor as has been discussed here recently). See Section 8 (Theorem 8.5) of this paper (arXiv).

Posted by: Tom Harris on June 3, 2021 11:57 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Thanks! I think you’re talking about polynomial functors in the sense of Chapter 1 Appendix A of MacDonald’s Symmetric Functions and Hall Polynomials. These are indeed quite different from the ‘polynomial functors’ that are all the rage now in category theory, and also somewhat different from the ‘polynomial species’ in my paper with Joe and Todd.

Posted by: John Baez on June 11, 2021 11:57 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Jack Morava let me post this email; I hope that someone can do something interesting with these ideas:

Dear John,

This is just to say your recent posting about plethories is very interesting, congratulations! BTW somewhere in Hazewinkel’s extensive writing he remarks that the usual multiplication on the big Witt vector ringscheme ( = representable endofunctor of commutative rings)

$A \mapsto (1 + tA[[t]])^\times := W_{\G_m}(A)$

(which sends $(1 + at) \cdot (1 + bt) \mapsto (1 + abt)$ ) [I think?]) can be generalized by somehow replacing the multiplicative group law $\G_m$ with any 1D commutative formal group law $F$ . Some time ago Ravenel and Wilson showed that the ring of unstable cohomology operations in complex cobordism theory is what you get if you plug Lazard’s universal 1D formal group law into the Witt vector construction.

Hazewinkel in fact once wrote to me about a (neither commutative nor noncommutative) Hopf algebra of formal diffeomorphisms of the noncommutative line (cooked up by physicists for applications to QED renormalization, which makes sense even though composition of power series with noncommuting coefficients isn’t associative), with interesting connections to the theory of quasisymmetric functions — which turn out to be much easier to work with than one might expect. I think this Hopf algebra shows up in the study of cohomology operations for cobordism of toric algebras as studied by Baker and Richter.

some references:

D Ravenel, W S Wilson, Hopf ring for complex cobordism, J Pure Appl Algebra 9 (1976/77) 241–280.

J Morava, Renormalization groupoids in algebraic topology, https://arxiv.org/abs/2007.16155

Posted by: John Baez on June 5, 2021 12:20 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Jack mentioned “the ring of unstable cohomology operations”. There’s a PhD thesis by William Mycroft, Unstable Cohomology Operations: Computational Aspects of Plethories, which takes up earlier work of Stacey and Whitehouse, the latter being his supervisor. This revolves around the fact that unstable cohomology operations form a plethory.

Posted by: David Corfield on June 11, 2021 10:24 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Interesting! I don’t really have the expertise to make reading that easy, but I have some gut feeling that there should be a classification theorem for plethories, and if anyone can explain to me how his plethories fit into it, I’d be grateful.

Here are the key steps:

1.Every plethory $P$ (over $\mathbb{Z}$ , let’s say) has a subset $A$ consisting of additive operators, which form a cocommutative co-algebra.

2.The plethory $\mathrm{Sym}(A)$ generated by $A$ maps injectively to $P$ . The image is the operators in $P$ which can be expressed as polynomials in additive operators (by the definition of the symmetric algebra). This is called the linear sub-plethory $L(P)$ of $P$ .

3.By some version of the Milnor-Moore theorem, $A$ is generated by its primitive and group-like element. So $A$ is some combination of a monoid and a Lie algebra. Translated to $L(P)$ , that means $L(P)$ consists of polynomial expressions in the derivation operations in $P$ and the ring-like operations in $P$ . Anyway, $A$ and hence $L(P)$ can typically be described in a very explicit way.

4.By Magnus Carlson’s theorem mentioned in another comment, if we were over $\mathbb{Q}$ instead of $\mathbb{Z}$ , we’d be done because we’d have $L(P)=P$ . But if we’re over $\mathbb{Z}$ , that is only true if we ignore denominators. To get the denominators right, I believe $P$ will be some kind of `amplification’ of $L(P)$ obtained by adjoining new operators which are polynomials expressions in the operators in $L(P)$ with rational coefficients but which are suitably integral-valued.

For example, the set of polynomials in binomial-coefficient functions $\binom{x}{n}$ forms a plethory $\mathrm{Bin}$ . The linear part is just the unit plethory $\mathbb{Z}[x]$ . Then $\mathrm{Bin}$ can be obtained from $\mathbb{Z}[x]$ by adding denominators to certain polynomials which satisfy congruence conditions.

I have this belief that all plethories can fit into this classification, or if not then that the classification can be tweaked so that they can. So when someone tells me they have a new plethory, I always want to know how to build it up in this way.

Love it if someone could do that for me with Mycroft’s plethories!

Posted by: James Borger on June 15, 2021 1:18 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Alas, write in haste, regret at leisure; apologies, the Witt product formula should have inverses in it for example.

If $E$ is a ring-spectrum and $X$ is a finite complex then $E^*(X)$ is represented by an infinite loopspace $\Omega^\infty E$ , and Hurewicz’s construction

(1)

E^*(X) \mapsto {Hom}_{E^*-{alg}}(E^*(\Omega^\infty E),E^*(X))

defines something like a comonad on nilpotent $E^*$ -algebras: for example if $E$ is complex $K$ -theory, we get the universal $\Lambda$ -ring, a.k.a. the big Witt vectors. These things are big and need topologies or something but I’ll leave that aside; but, in general, *unstable operations on multiplicative cohomology theories are a source of a lot of things that seem close to plethories.

Steve Wilson’s thesis showed that $MU^*(\Omega^\infty MU)$ is torsion-free and so can be unwound in terms of Witt-vector-like formulae. I’m afraid I can’t provide a better reference for Hazewinkel’s remark than that.

In other fumbles, I should have said toric manifold (in the sense of Davis and Januszkiewicz) rather than toric algebra. Maybe I should also say that this approach doesn’t seem to work very well for the sphere spectrum.

Posted by: jackjohnson on June 5, 2021 2:00 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Hooray! I’d say at long last, but I didn’t know it was in the works. I look forward to having a look. I agree it’s remarkable how a free thing on a single generator becomes so interesting when decategorified. If this happens in this basic situation, it must happen all over the place if you know how to see it.

Congratulations to everyone!

Posted by: James Borger on June 6, 2021 5:44 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

When someone comes to write the history of this paper, they should also look at the discussion of 11 years ago, in the thread of John’s post This Week’s Finds in Mathematical Physics (Week 299) with James making predictions:

(1) There is a good categorification of the notion of ‘ring’, or maybe ‘semi-ring’. This probably exists already. Let’s call it a ring-category. There’s probably a good notion of the 2-category of ring-categories. (2) There is a 2-monad 2 $\Lambda$ on the 2-category of ring-categories such that the free 2 $\Lambda$ -ring-category on one object is the category of representations of the general linear group. In other words, the category of such representations admits certain extra structure which allows us to make sense of an action of it on a ring-category. (3) The category of vector bundles on a ringed topos should naturally have an action of the 2-monad 2 $\Lambda$ . (4) The 2-category of algebras for this 2-monad 2 $\Lambda$ is the right abstract context for talking about the splitting principle and, more generally, undecategorified K-theory.

And also an nLab discussion on plethysm.

Posted by: David Corfield on June 13, 2021 8:25 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Thanks, David! I’d completely forgotten those predictions. Here’s what our paper says about them.

(1): Joe and I looked at a wide range of notions of concepts of ‘ring-category’ or really ‘rig-category’. There are a lot of useful concepts along these lines, and I don’t know one that “rules them all and in the darkness binds them”. So, I suspect there’s an interesting 3-category of 2-categories of differently defined rig-categories.

However, when Todd rejoined the project, we decided to focus on $\mathsf{Schur}$ and one specific concept of rig-category, which — purely for the purposes of this paper — we call a ‘2-rig’. So we study a 2-category $\mathbf{2Rig}$ but do not claim that it’s the ultimate solution to all questions in this vicinity. For example, it’s defined relative to a chosen field of characteristic zero. It’s easy to remove the characteristic zero assumption from the definition, but some of our more interesting results rely on it, and would change in interesting ways without it.

(2) In the case of rings, as Jim Borger must have known, there is for each plethory $B$ a left adjoint monad $\Psi_B \colon \mathsf{Ring} \to \mathsf{Ring}$ . Indeed we can efficiently define a plethory to be such a left adjoint monad, and we can recover $B$ from that. When $B = \Lambda$ this monad is the ‘free $\lambda$ -ring’ monad.

But $\Lambda$ is a decategorification of $\mathsf{Schur}$ , the free 2-rig on one generator. We show that $\mathsf{Schur}$ is a 2-plethory, and we show that there is a corresponding left adjoint 2-monad $\Psi_{\mathsf{Schur}} \colon \mathbf{2Rig} \to \mathbf{2Rig}$ .

We focus, however, not on $\Psi_{\mathsf{Schur}}$ but on its right adjoint, the right adjoint 2-comonad $\Phi_{\mathsf{Schur}} \colon \mathbf{2Rig} \to \mathbf{2Rig}$ . This is for technical reasons: we found it easier to describe and work with.

So, we did not get into studying everything Jim guessed about $\Psi_{\mathsf{Schur}}$ , which should be a version of what he called $2\Lambda$ .

(3), (4): Similarly, we did not get into all of this. But the category of vector bundles on a ringed topos should definitely be a 2-rig according to our definition of ‘2-rig’. To be really precise: I’m 100% confident of this in the case of vector bundles on a topological space, and I don’t see any reason for it to fail in this more general situation.

Anyway, it should be quite doable now to check the rest of Jim’s predictions, at least for our chosen concept of ‘2-rig’.

Posted by: John Baez on June 13, 2021 9:24 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Ah! The right adjoint $\Phi_{\mathrm{Schur}}$ is the big Witt vector functor! Or at least its decategorification is.

Did you think about how to describe the image of the category of finite dimensional vector spaces under $\Phi_{\mathrm{Schur}}$ ? (Maybe Davydov did something like this in different language. I talked with Oded Yacobi about these things once…)

The answer would be a categorification of what I call $W_{\mathrm{Sch}}(\mathbb{N})$ , which has a beautiful description.

Posted by: James Borger on June 15, 2021 1:43 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Taking a closer look at the article

Imma Gálvez-Carrillo, Joachim Kock, and Andrew Tonks. Homotopy linear algebra. Proc. Roy. Soc. Edinburgh Sect. A, 148(2):293–325, 2018 (arXiv:1602.05082),

the authors provide what will play the role of the category of finite vector spaces by (p. 5), $\mathsf{lin}$ , the $(\infty,1)$ -category of slices of, $\mathcal{F}$ , the $(\infty, 1)$ -category of finite $\infty$ -groupoids, $\mathcal{F}/\alpha$ , and morphisms given by finite spans, $\alpha \leftarrow \mu \to \beta$ .

(Variants are given to correspond to all vector spaces and profinite-dimensional vector spaces.)

Section 8 gives us a cardinality, which will map $\mathsf{lin}$ to $\mathsf{FinVect}$ .

So what would a variant of the current $\mathsf{Poly}$ look like, comprised of $(\infty, 1)$ -functors from $\mathsf{S}$ to $\mathsf{lin}$ (maybe which are eventually trivial)?

Over the rationals, this cardinality is surjective to rational vector spaces and non-negative maps.

Posted by: David Corfield on June 13, 2021 10:58 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

This paper takes the groupoidification program and pushes it up to $\infty$ -groupoids, so the basic idea is very familiar to me, though I didn’t have the technical prowess to formalize it all. The idea is to generalize Joyal’s species, or more generally stuff types, to the world of homotopy theory.

I believe that $(\infty,1)$ -functors $f \colon \mathsf{S} \to \mathsf{lin}$ correspond to infinity-groupoids over $\mathsf{S}$ . In other words, they describe ways of equipping finite sets with ∞-stuff. Another way to think about them is as fibrations whose base space is the space of finite sets.

These are very nice things, and the maps between these things, defined using spans, are also very nice. They resemble linear operators. In the 1-groupoid case James Dolan and I called them ‘stuff operators’.

Posted by: John Baez on June 13, 2021 11:10 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

So $n: \mathsf{S}$ would be sent to a slice $\mathcal{F}/\alpha$ , and elements of $Sym(n)$ would act via spans of finite $\infty$ -groupoids $\alpha \leftarrow \mu \to \alpha$ .

Since ordinary representations of $Sym(n)$ require negative numbers, I’d imagine a further step of group completion is still needed. As some people once said:

…to properly categorify subtraction, we need to categorify not just once but infinitely many times!

Posted by: David Corfield on June 14, 2021 8:20 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Permutation representations are meagre in relation to all plain linear representations, however virtual permutation representations make up far more of the virtual linear representations.

Posted by: David Corfield on June 15, 2021 7:25 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Perhaps this focus on finite $\infty$ -groupoids relates to the choice in the notes by Barwick mentioned above, where $\mathsf{Perf}_{\mathbb{C}}$ is

the $(\infty,1)$ -category of perfect $H \mathbb{C}$ -modules – that is, of $H \mathbb{C}$ -modules with finitely many homotopy groups, all of which are finite-dimensional.

Then $\mathsf{Perf}_{\mathbb{C}}[x]$ is the subcategory of $Fun(\mathsf{S}, \mathsf{Perf}_{\mathbb{C}})$ which vanish for large enough $n$ .

This is presumably some kind of free $(\infty, 2)$ -rig on one generator.

Posted by: David Corfield on June 14, 2021 11:43 AM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

Congratulation with the paper! That’s a whole lot of interesting stuff on many of my favourite topics.

I wish I understood plethories, to start with, so that I had better chances of understanding also 2-plethories. What I have seen so far already makes me think that it is a beautiful theory!

Since David has summoned me – thanks for even thinking of me! and thanks for the ping – I now write something, but I am afraid it is mostly digression from the main themes of the thread, and even digression in two directions.

First I can briefly tell you about the thesis work of my former student Alex Cebrian on plethysm. Second I can give a status rapport on symmetric functions in objective combinatorics and objective linear algebra (upcoming Gálvez-Kock-Tonks papers). It is a categorification in a slightly different spirit, and so far it is mostly footwork. We do not yet know how to deal with lambda rings or plethories. And what is more irritating for us: we don’t know how to do the Schur basis :-( (…as I pestered both John and Todd about at the CT19 in Edinburgh.) In the terminology of James further up this thread, it could be that our theory is more geared towards axial vector spaces(?), and that that’s why we find the Schur basis so difficult…

Posted by: Joachim Kock on June 24, 2021 9:28 PM | Permalink | Reply to this

Re: Schur Functors and Categorified Plethysm

$MathML-enabled post (click for more details).$

A paper relating plethysms to Baez and Dolan on opetopes. What more could you want, John?

Ralph M. Kaufmann, Michael Monaco, Plethysm Products, Element and Plus Constructions (arXiv:2211.11946)

Posted by: David Corfield on November 23, 2022 10:06 AM | Permalink | Reply to this

Read the post The Free 2-Rig on One Object
Weblog: The n-Category Café
Excerpt: What is a 2-rig, and why is the free 2-rig on one object the category of Schur functors?
Tracked: October 2, 2023 10:56 AM

The n-Category Café

Skip to the Main Content

June 2, 2021

Schur Functors and Categorified Plethysm

Posted by John Baez

The history

Schur functors and categorified plethysm

Outline of the paper

Some Related Entries

79 Comments & 1 Trackback

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

GRT

Re: GRT

Re: GRT

Re: GRT

Re: GRT

Re: GRT

Re: GRT

Re: GRT

Re: GRT

Re: GRT

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm

Re: Schur Functors and Categorified Plethysm