Weakly Globular Double Categories: a Model for Bicategories
Posted by Emily Riehl
guest post by Claire Ott and Emma Phillips as part of the Adjoint School for Applied Category Theory 2021.
As anyone who has worked with bicategories can tell you, checking coherence diagrams can hold up the completion of a proof for weeks. Paoli and Pronk have defined weakly globular double categories, a simplicial model of bicategories which is a sub-2-category of the 2-category of double categories. Today, we’ll introduce weakly globular double categories and briefly talk about the advantage of this model. We’ll also take a look at an application of this model: the SIRS model of infectious disease.
What is a weakly globular double category?
We’d like to find a sub-2-category of double categories that is biequivalent to the 2-category of bicategories. There are several reasons to want this model of bicategories, which we’ll talk about below. To compare bicategories and double categories, we’re going to consider them as objects in . This will enable us to develop a model of bicategories that lives between strict 2-categories and double categories. Two facts are going to help us develop this model:
Fact 1. is the horizontal nerve of a double category iff the Segal maps are isomorphisms.
Fact 2. is the nerve of a strict 2-category iff is discrete and the Segal maps are isomorphisms.
Since bicategories are weak 2-categories, it seems that we should be able to weaken the conditions of Fact 2 to get a model of bicategories in . By Fact 1, if we want this model to land in double categories, we should keep the requirement that the Segal maps are isomorphisms. Hence we want a property that’s a little less strong than being discrete.
We start with a weak gloublarity condition: we require that there is an equivalence of categories , where is the discrete category of the path components of . In the corresponding double category, the weak globularity condition amounts to , the category of objects and vertical arrows, being a posetal groupoid; that is, every pair of objects has at most one arrow between them, which is an isomorphism.
When we define the fundamental bicategory of a weakly globular double category , meaning the bicategory associated to (see 8.1 here), we will define the objects to be the connected components of and the arrows to be the horizontal morphisms of . However, this creates a potential problem - how do we compose two morphisms whose codomain and domain are in the same component but don’t agree?
To solve this, we define an induced Segal maps condition: we require that for all , induces an equivalence of categories . This condition answers the composition problem because it allows us to fill in staircases, meaning paths of alternating horizontal and vertical arrows, with invertible 2-cells:
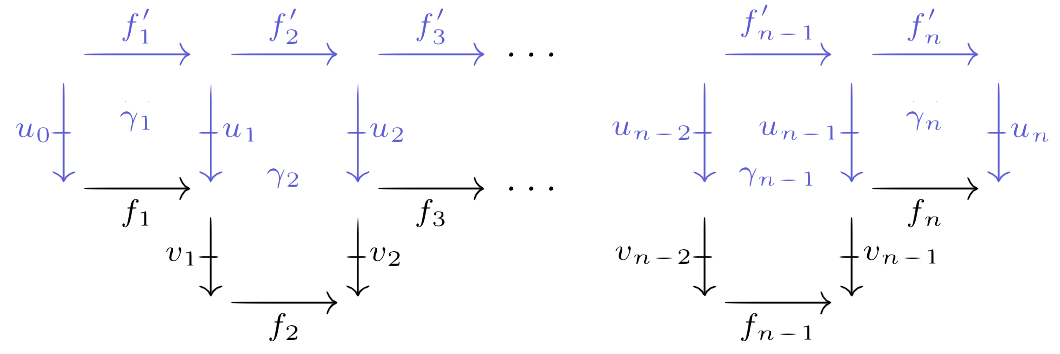
This lift of the horizontal maps will give us our composite in the fundamental bicategory.
Finally we have our definition of a weakly globular double category: is a weakly gloublar double category if and only if
- the Segal maps are isomorphisms (i.e., is a double category);
- (weak globularity condition) there is an equivalence of categories , where is the discrete category of the path components of ;
- (induced Segal maps condition) for all , induces an equivalence of categories .
We then have the following theorem, which you can read more about here:
Theorem 1. There is a biequivalence of 2-categories between the 2-category of weakly globular double categories with (double) pseudofunctors and vertical transformations and the 2-category of bicategories with normal homomorphisms1 and icons :
Why study weakly globular double categories?
We’ll now try to convince you of why you should be interested in this model of bicategories. Between strict 2-categories, bicategories, and double categories, bicategories seem to show up most often in the wild. Even in pure mathematics, requiring that composition be strictly associative is often too strong of a condition. However, bicategories are also the most difficult to work with, since we have to check several coherence diagrams.
When we use weakly globular double categories, however, the coherence data is encoded in the combinatorial data of the simplicial structure. Hence when defining a bicategory, we can simply give a double category that adheres to the weak globularity and induced Segal maps conditions.
Even so, you may be thinking that while dealing with bicategory coherence diagrams can be unpleasant, they’re not so terrible that it’s worth learning a new model. The real power of this model, however, comes when we extend this notion to higher categories. Checking the coherence diagrams for tricategories is rather terrible, and there’s not even a clear notion of what the coherence diagrams should be for -categories for . In her book, Paoli proves that weakly globular n-fold categories model weak n-categories. As in the case when , the weak globularity weakens the higher categorical structures of strict -categories. For , instead of the -cells forming a set as they do in a strict -category, they form a -fold category which is suitably equivalent to a discrete one.
How do weakly globular double categories show up in applications?
To get a better understanding of what these weakly globular double categories can look like and what they might be used for, we want to introduce an example of marked paths of token placements in Petri nets. In these categories, morphisms only exist between objects with the same underlying Petri net, so we will focus on a category built on one specific net for this example: the SIRS model of infectious disease. We will call this weakly globular double category . Though we have not explicitly constructed this double category using the functor , we have drawn inspiration from the double category of marked paths in Paoli and Pronk, 8.2.
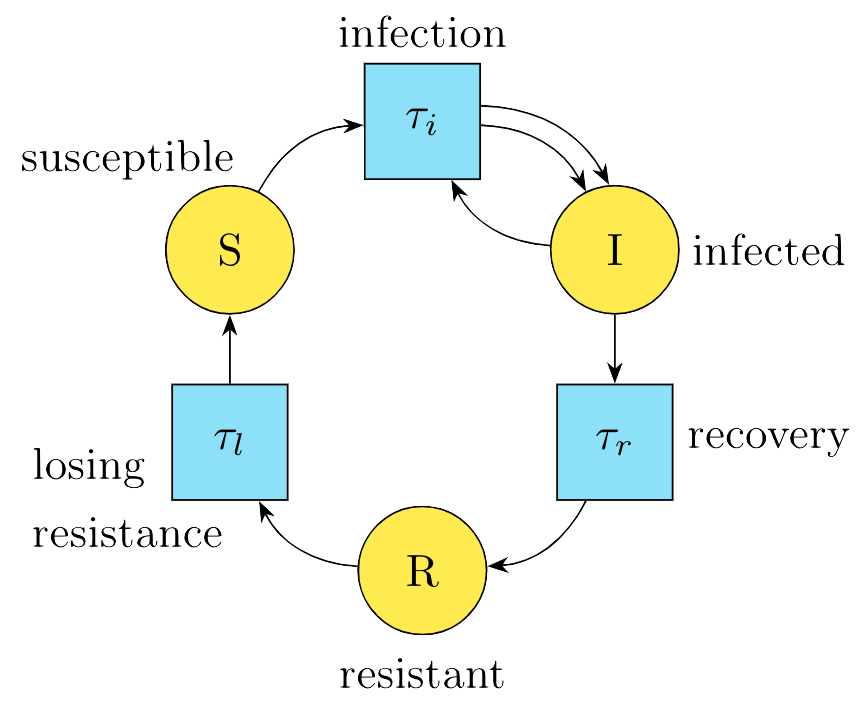
We would like to use token placements to model a group of three people which can be susceptible (), infected () or resistant (). A token placement is a linear combination of places, i.e the placement signifies two susceptible and one infected persons. A firing can happen at a transition, which are in our example infection (), recovery () and loosing resistance (). Each transition has a source and a target which are again linear combinations of places and the condition for a firing is that enough tokens are placed at the transition’s source. In our example there could initially occur a firing at leading to the placement or at , but not at .
Firings can be combined if the state after one firing is compatible with the next firing. This combination will have its own source and target which does not necessarily have to be the same as the first firing’s source and the last firing’s target. For example has source and target . The order of the firings is also significant.
We want to construct to capture paths of token placements which can occur through consecutive firings. In our example, one such path could be , meaning we start with two susceptible and one infected person, which infects one of those two. Then one of the two infected people recovers, and next the other one recovers. One point to note is that we cannot distinguish tokens by means other than their placement, and so the scenario where the first infected person recovers first looks the same as the second infected person recovering first.
The objects of are marked paths, marking one token placement of the path. For our example, the marked paths are all unique objects in . Each object can be interpreted as a path of events that led to and follow from a chosen state of susceptible, infected, and resistant people.
Therefore we might be interested in all objects with the same fixed state, i.e. token placement. The vertical morphisms in are unique and exist between any two objects with the same marked token placement. For example, if we want to know the possible history and future for the state of two susceptible people and one infected person, we could look at all vertical morphisms to or from the object . Our potential vertical morphisms would include the following:
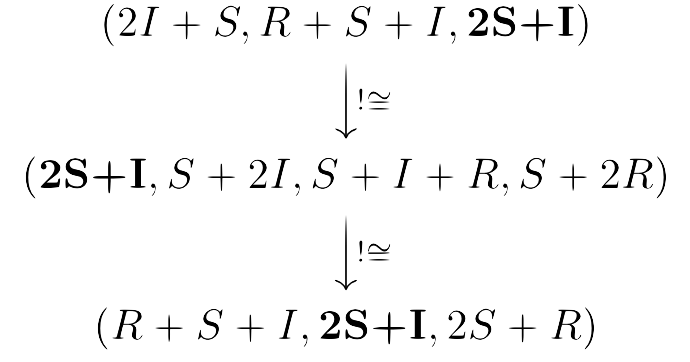
Horizontal morphisms only exist between pairs of objects with the same underlying path. There is exactly one horizontal morphism between each of these pairs, with the direction of the morphisms the same as the path’s direction. Horizontal morphisms are labeled by paths with two placements marked. For example refers to the following morphism:
Note that there is no horizontal morphism in the opposite direction even though there is a path from to .
Using vertical and horizontal morphisms we get 2-cells of the following form:
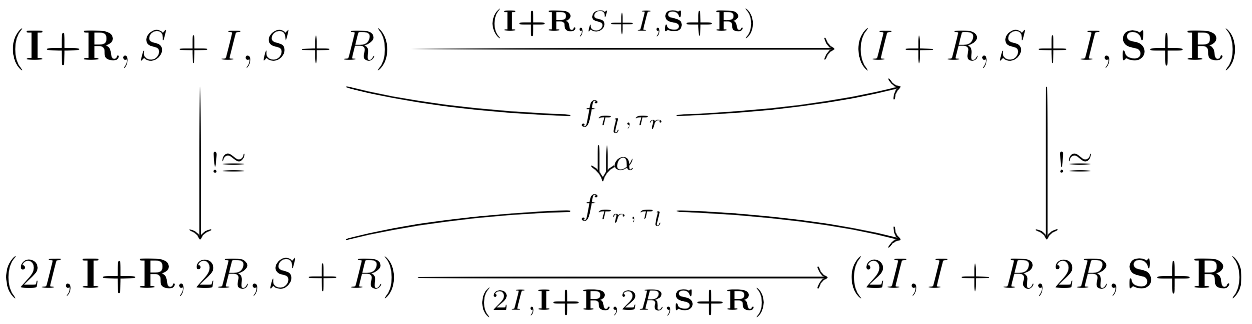
In order to make our horizontal composition strictly associative, we have a chosen way to compose a string of horizontal maps which is encoded in the maps in the center of the diagram. The 2-cell witnesses the existence of alternate paths between two fixed states. In , all 2-cells are invertible.
We can see that is indeed a weakly globular double-category. The weak globularity condition is immediate, since the only vertical morphisms are isomorphisms and every pair of objects has at most one vertical morphism between them. In order to see that the induced Segal maps condition holds, consider an example staircase:

We fill in the top row of the staircase by creating a path of events built from the sequences encoded in the horizontal morphisms.
1 These are pseudofunctors of bicategories which preserve identities strictly. ↩

Re: Weakly globular double categories: a model for bicategories
Cool! You say “horizontal morphisms only exist between pairs of objects with the same underlying path” but I don’t get what the horizontal morphisms actually are in this example. You give an example of a horizontal morphism and maybe you even quickly say what they are in general, but I’m not getting it.