The n-Category Café

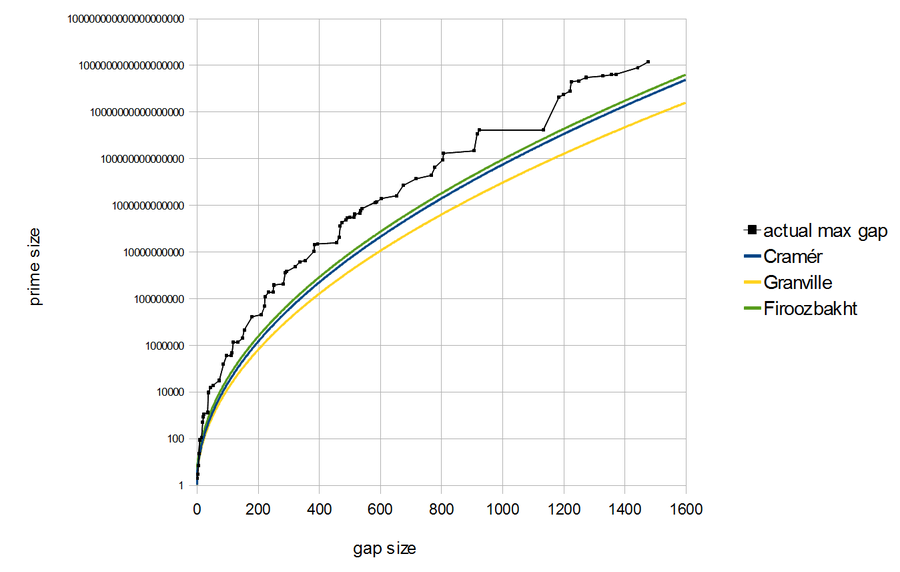
Firoozbakht’s conjecture is a way of saying the gaps between successive primes don’t get too big too fast. As you can see here, it’s stronger than Cramér’s or Granville’s conjectures on prime gaps — and it gets scarily close to being wrong at times, like when the largest prime gap jumps from 924 to 1132 at the prime 1693182318746371 — you can see that big horizontal black line above.

Farideh Firoozbakht checked her conjecture up to about 4 trillion using a table of large gaps between primes: those are what could make the conjecture false. In 2015 Alexei Kourbatov checked it up to 4 quintillion, in this paper here:

• Alexei Kourbatov, Verification of the Firoozbakht conjecture for primes up to four quintillion, International Mathematical Forum 10 (2015), 283–288.

Now Kourbatov claims to have checked Firoozbakht’s conjecture for all primes less than $2^64$, which is a bit over 18 quadrillion. The work is on a website that links to someone’s table of big prime gaps, and the link seems a bit broken:

• Alexei Kourbatov, The Firoozbakht conjecture.

Maybe this table of prime gaps will do the job.

If true, Firoozbakht’s conjecture will imply a lot of good stuff, listed in this paper by Ferreira and Mariano:

• Luan Alberto Ferreira and Hugo Luiz Mariano, Some consequences of the Firoozbakht’s conjecture.

For example: there are at least 2 primes between consecutive square numbers, and at least 4 between consecutive cubes.

It’s known that the Riemann Hypothesis implies the $n$th prime gap is eventually less than $\sqrt{p_n} \, \ln p_n$, where $p_n$ is the $n$th prime. Firoozbakht’s conjecture implies something much stronger: it’s eventually less than

$$c(\ln p_n)^2$$

where you can choose $c$ to be any constant bigger than 1. This is Theorem 2.2 in Ferreira and Mariano’s paper.

Nobody knows how to prove Firoozbakht’s conjecture using the Riemann Hypothesis. But conversely, it seems nobody has shown Firoozbakht implies Riemann!

There are even some good theoretical reasons for believing Firoozbakht’s conjecture is false! Granville has a nice probabilistic model of the behavior of primes that predicts that there are infinitely many gaps arbitrarily close to

$$2e^{-\gamma} \, (\ln p_n)^2 \approx 1.1229 \, (\ln p_n)^2$$

in width. Firoozbakht’s conjecture, on the other hand, implies they’re eventually all significantly smaller than this, as I mentioned above.

For more on Granville’s probabilistic model of primes and its consequences for the largest prime gaps, see:

• Terry Tao, Large prime gaps and probabilistic models, What’s New, August 26, 2019.

• Andrew Granville and Allysa Lumley, Primes in short intervals: heuristics and calculations.

Farideh Firoozbakht, alas, died in 2019 at the age of 57. She studied pharmacology and later mathematics at the University of Isfahan, and later taught mathematics at that university. That, and her conjecture, is all I know about her. I wish I could ask her how she came up with her conjecture, and ask her a bit about what her life was like.

If anyone knows, please tell me!

I thank Maarten Morier for telling me about Firoozbakht’s conjecture.