The Kuramoto–Sivashinsky Equation (Part 1)
Posted by John Baez
I love this movie showing a solution of the Kuramoto–Sivashinsky equation, made by Thien An. If you haven’t seen her great math images on Twitter, check them out!
I hadn’t known about this equation, and it looked completely crazy to me at first. But it turns out to be important, because it’s one of the simplest partial differential equations that exhibits chaotic behavior and an ‘arrow of time’: that is, a difference between the future and past.
I love this movie showing a solution of the Kuramoto–Sivashinsky equation, made by Thien An. If you haven’t seen her great math images on Twitter, check them out!
I hadn’t known about this equation, and it looked completely crazy to me at first. But it turns out to be important, because it’s one of the simplest partial differential equations that exhibits chaotic behavior.
As the image scrolls to the left, you’re seeing how a real-valued function of two real variables changes with the passage of time. The vertical direction is ‘space’, while the horizontal direction is time,
Near the end of this post I’ll make some conjectures about the Kuramoto–Sivashinsky equation. The first one is very simple: as time passes, stripes appear and merge, but they never disappear or split.
The behavior of these stripes makes the Kuramoto–Sivashinsky equation an excellent playground for thinking about how differential equations can describe ‘things’ with some individuality, even though their solutions are just smooth functions. But to test my conjectures, I could really use help from people who are good at numerical computation or creating mathematical images! (If you’re interested, you should check out the comments on my Azimuth blog article.)
First let me review some known stuff. You can skip this and go straight to the conjectures if you want, but some terms might not make sense.
Review
For starters, note that these stripes seem to appear out of nowhere. That’s because this system is chaotic: small ripples get amplified. This is especially true of ripples with a certain wavelength: roughly , as we’ll see later.
And yet while solutions of the Kuramoto–Sivanshinsky equation are chaotic, they have a certain repetitive character. That is, they don’t do completely novel things; they seem to keep doing the same general sort of thing. The world this equation describes has an arrow of time, but it’s ultimately rather boring compared to ours.
The reason is that all smooth solutions of the Kuramoto–Sivanshinsky equation quickly approach a certain finite-dimensional manifold of solutions, called an ‘inertial manifold’. The dynamics on the inertial manifold is chaotic. And sitting inside it is a set called an ‘attractor’, which all solutions approach. This attractor is probably a fractal. This attractor describes the complete repertoire of what you’ll see solutions do if you wait a long time.
Some mathematicians have put a lot of work into proving these things, but let’s see how much we can understand without doing anything too hard.
Written out with a bit less jargon, the Kuramoto–Sivashinky equation says
or in more compressed notation,
To understand it, first remember the heat equation:
This describes how heat spreads out. That is: if is the temperature of an iron rod at position at time , the heat equation describes how this temperature function flattens out as time passes and heat spreads.
But the Kuramoto–Sivashinsky equation more closely resembles the time-reversed heat equation
This equation describes how, running a movie of a hot iron rod backward, heat tends to bunch up rather than smear out! Small regions of different temperature, either hotter or colder than their surroundings, will tend to amplify.
This accounts for the chaotic behavior of the Kuramoto–Sivashinsky equation: small stripes emerge as if out of thin air and then grow larger. But what keeps these stripes from growing uncontrollably?
The next term in the equation helps. If we have
then very sharp spikes in tend to get damped out exponentially.
To see this, it helps to bring in a bit more muscle: Fourier series. We can easily solve the heat equation if our iron rod is the interval and we demand that its temperature is the same at both ends:
This lets us write the temperature function in terms of the functions like this:
for some functions . Then the heat equation gives
and we can easily solve these equations and get
and thus
So, each function decays exponentially as time goes on, and the so-called ‘high-frequency modes’, with big, get damped really fast due to that factor. This is why heat smears out as time goes on.
If we solve the time-reversed heat equation the same way we get
so now high-frequency modes get exponentially amplified. The time-reversed heat equation is a very unstable: if you change the initial data a little bit by adding a small amount of some high-frequency function, it will make an enormous difference as time goes by.
What keeps things from going completely out of control? The next term in the equation helps:
This is still linear so we can still solve it using Fourier series. Now we get
Since , none of the modes grows exponentially. In fact, all the modes decay exponentially except for three: . These will be constant in time. So, any solution will approach a constant as time goes on!
We can make the story more interesting if we don’t require our rod to have length . Say it has length . We can write periodic functions on the interval as linear combinations of functions where now the frequencies aren’t integers: instead
for integers . The longer our rod, the lower these frequencies can be. The rest of the math works almost the same: we get
but we have to remember . The modes with will grow exponentially, while the rest will decay exponentially or stay constant. Note that only for . So, modes with these frequencies grow exponentially. Modes with decay exponentially.
If , all the frequencies are integers times , which is bigger than , so no modes grow exponentially — and indeed all solutions approach a constant! But as you look at longer and longer rods, you get more and more modes that grow exponentially. The number of these will be roughly proportional to , though they will ‘pop into existence’ at certain specific values of .
Which exponentially growing modes grow the fastest? These are the ones that make as large as possible, so they happen near where
namely . The wavelength of a mode is , so these fastest-growing modes have wavelength close to .
In short, our equation has a certain length scale where the instability is most pronounced: temperature waves with about this wavelength grow fastest.
All this is very easy to work out in as much detail as we want, because our equation so far is linear. The full-fledged Kuramoto–Sivashinsky equation
is a lot harder. And yet some features of the linear version remain, which is why it was worth spending time on that version.
For example, I believe the stripes we see in the movie above have width roughly . Stripes of roughly this width tend to get amplified. Why don’t they keep on growing taller forever? Apparently the nonlinear term prevents it. But this is not obvious. Indeed, it’s conjectured that if you solve the Kuramoto–Sivashinsky equation starting with a bounded smooth function , the solution will remain bounded by a constant. But this has not been proved — or at least it was not proved as of 2000, when this very nice article was written:
- Encyclopedia of Mathematics, Kuramoto–Sivashinsky equation.
The inertial manifold
The most fascinating fact about the Kuramoto–Sivashinsky equation is that for any fixed length , it has a finite-dimensional manifold of solutions such that every solution approaches one of these, exponentially fast! So, while this equation really describes an infinite-dimensional dynamical system, as its solutions move closer and closer to the solutions of some finite-dimensional dynamical system. This finite-dimensional system contains all the information about the patterns we’re seeing in Thien An’s movie.
As I mentioned, the manifold is called an ‘inertial manifold’. This is a general concept in dynamical systems theory:
- Wikipedia, Inertial manifold.
To make these ideas precise we need to choose a notion of distance between two solutions at a given time. A good choice uses the norm for periodic functions on :
Functions on with finite norm form a Hilbert space called . If we start with any function in this Hilbert space we get a solution of the Kuramoto–Sivashinsky equation such that the function is in this Hilbert space at all later times . Furthermore, this function is smooth, even analytic, for all later times:
- P. Collet, J.-P. Eckmann, H. Epstein and J. Stubbe, Analyticity for the Kuramoto–Sivashinsky equation, Physica D 67 (1993), 321–326.
This smoothing property is well-known for the heat equation, but it’s much less obvious here!
This work also shows that the Kuramoto–Sivashinsky equation defines a dynamical system on the Hilbert space . And based on earlier work by other mathematicians, Temam and Wang have heroically shown that this Hilbert space contains an inertial manifold of dimension bounded by some constant times
- Roger Temam and Xiao Ming Wang, Estimates on the lowest dimension of inertial manifolds for the Kuramoto-Sivashinsky equation in the general case, Differential and Integral Equations 7 (1994), 1095–1108.
I conjecture that in reality its dimension grows roughly linearly with . Why? We’ve just seen this is true for the linearized version of the Kuramoto–Sivashinsky equation: all modes with frequency get damped exponentially, but since there’s one mode for each integer , and , these modes correspond to integers with . So, there are of these modes. In short, for the linearized Kuramoto–Sivashinsky equation the inertial manifold has dimension about .
This evidence is rather weak, since it completely ignores the nonlinearity of the Kuramoto–Sivashinsky equation. I would not be shocked if the dimension of the inertial manifold grew at some other rate than linearly with .
Sitting inside the inertial manifold is an attractor, the smallest set that all solutions approach. This is probably a fractal, since that’s true of many chaotic systems. So besides trying to estimate the dimension of the inertial manifold, which is an integer we should try to estimate the dimension of this attractor, which may not be an integer!
There have been some nice numerical experiments studying solutions of the Kuramoto–Sivashinsky equation for various values of , seeing how they get more complicated as increases. For small , every solution approaches a constant, just as in the linearized version. For larger we get periodic solutions, and as continues to increase we get period doubling and finally chaos — a typical behavior for dynamical systems. But that’s just the start. For details, read this:
- Demetrios T. Papageorgiou and Yiorgos S. Smyrlis, The route to chaos for the Kuramoto–Sivashinsky equation, Theoretical and Computational Fluid Dynamics 3 (1991), 15–42.
I’ll warn you that they use a slightly different formalism. Instead of changing the length , they keep it equal to and change the equation, like this:
for some number they call the ‘viscosity’. It’s just a different way of describing the same business, so if I had more energy I could figure out the relation between and and tell you at which length chaos first kicks in. But I won’t now. Instead, I want to make some conjectures.
Conjectures
There should be some fairly well-defined notion of a ‘stripe’ for the Kuramoto–Sivashinsky equations: you can see the stripes form and merge here, and if we can define them, we can count them and say precisely when they’re born and when they merge:
For now I will define a ‘stripe’ as follows. At any time, a solution of the Kuramoto–Sivashinsky gives a periodic function on the interval We can think of this as a function on the circle. A stripe will be a maximal closed subinterval of the circle on which This definition depends on a constant and it’s up to you to pick a value of the constant that makes my conjectures true — or at least, almost true!
So, here are the conjectures:
First, I conjecture that if is large enough, almost every non-negative solution in the inertial manifold has a finite number of stripes at any time and that while they can appear and merge as we increase they can never split or disappear.
(Here ‘almost every’ is in the usual sense of measure theory. There are certainly solutions of the Kuramoto–Sivashinsky equation that don’t have stripes that appear and merge, like constant solutions. These solutions may lie on the inertial manifold, but I’m claiming they are rare.)
I also conjecture that the time-averaged number of stripes is asymptotically proportional to as for almost every nonnegative solution on the inertial manifold. The constant of proportionality shouldn’t depend on the solution we pick, except for solutions in some set of measure zero. It will, however, depend on our precise definition of ‘stripe’, e.g. our choice of the constant
I also conjecture that there’s a well-defined time average of the rate at which new stripes form, which is also asymptotically proportional to and independent of which solution we pick, except for solutions in a set of measure zero.
I also conjecture that this rate equals the time-averaged rate at which stripes merge, while the time-averaged rate at which stripes disappear or split is zero.
These conjectures are rather bold, but of course there are various fallback positions if they fail.
How can we test these conjectures? It’s hard to explicitly describe solutions that are actually on the inertial manifold, but by definition, any solution keeps getting closer to the inertial manifold at an exponential rate. Thus, it should behave similarly to solutions that are on the inertial manifold, after we wait long enough. So, I’ll conjecture that the above properties hold not only for almost every solution on the inertial manifold, but for typical solutions that start near the inertial manifold… as long as we wait long enough when doing our time averages.
If you feel like working on this, here are some things I’d really like:
- Images like Thien An’s but with various choices of To create these, maybe start with
and run it for long enough to ‘settle down’ — that is, get near the inertial manifold.
A time-averaged count of the average number of stripes for various choices of I’m conjecturing that this is asymptotically proportional to for large
Time-averaged counts of the rates at which stripes are born, merge, split, and die — again for various choices of I’m conjecturing that the first two are asymptotically proportional to for large and that they’re equal. I’m conjecturing that the last two are zero, or tiny.
If someone gets into this, maybe we could submit a short paper to Experimental Mathematics. I’ve been browsing papers on the Kuramoto–Sivashinsky equations, and I haven’t yet seen anything that gets into as much detail on what solutions look like as I’m trying to do here.
The arrow of time
One more thing. I forgot to emphasize that the dynamical system on the Hilbert space is not reversible: we can evolve a solution forwards in time and it will stay in this Hilbert space, but not backwards in time. This is very well-known for the heat equation; the point is that solutions get smoother as we run them forward, but when we run them backward they typically get more wild and eventually their norm blows up.
What makes this especially interesting is that the dynamical system on the inertial manifold probably is reversible. As long as this manifold is compact, it must be: any smooth vector field on a compact manifold generates a ‘flow’ that you can run forward or backward in time.
And yet, even if this flow is reversible, as I suspect it is, it doesn’t resemble its time-reversed version! It has an ‘arrow of time’ built in, since bumps are born and merge much more often than they merge and split.
So, if my guesses are right, the inertial manifold for the Kuramoto–Sivashinsky equation describes a deterministic universe where time evolution is reversible — and yet the future doesn’t look like the past, because the dynamics carry the imprint of the irreversible dynamics of the Kuramoto–Sivashinsky equation on the larger Hilbert space of all solutions.
A warning
If you want to help me, the following may be useful. I believe the stripes are ‘bumps’, that is, regions where for some positive constant That would make them easy to define. I was shocked when Steve Huntsman did some calculations and produced a picture showing a solution where :
Here the stripes are not mere bumps: they are regions where, as we increase , the solution first becomes large and negative and then becomes large and positive!
After massive confusion I realized that Steve was using some MATLAB code adapted from this website:
• Mathab Lak, Test case for PDEs: Kuramoto–Sivashinksy, Crank-Nicolson/Adams-Bashforth (CNAB2) timestepping.
and this code solves a different version of the Kuramoto–Sivashinksy equations, the so-called derivative form:
If satisfies the integral form of the Kuramoto–Sivashinksy equation, which is the one I’ve been talking about all along:
then its derivative
satisfies the derivative form.
So, the two equations are related, but you have to be careful because some of their properties are quite different! For the integral form, the cross-section of a typical stripe looks very roughly like this:
but for the derivative form it looks more like this:
You can grab Steve Huntsman’s MATLAB code here, but beware: this program solves the derivative form! Many of Steve’s pictures in comments on Azimuth — indeed, all of them so far — show solutions of the derivative form. In particular, the phenomenon he discovered of stripes tending to move at a constant nonzero velocity seems to be special to the derivative form of the Kuramoto–Sivashinsky equation. I’ll say more about this next time.

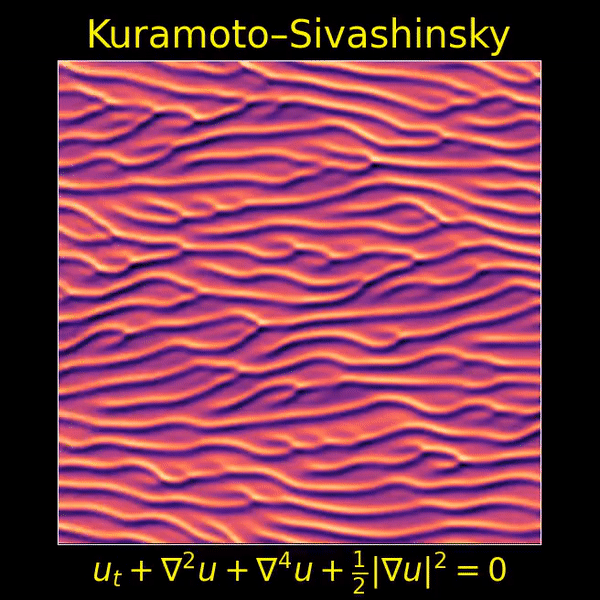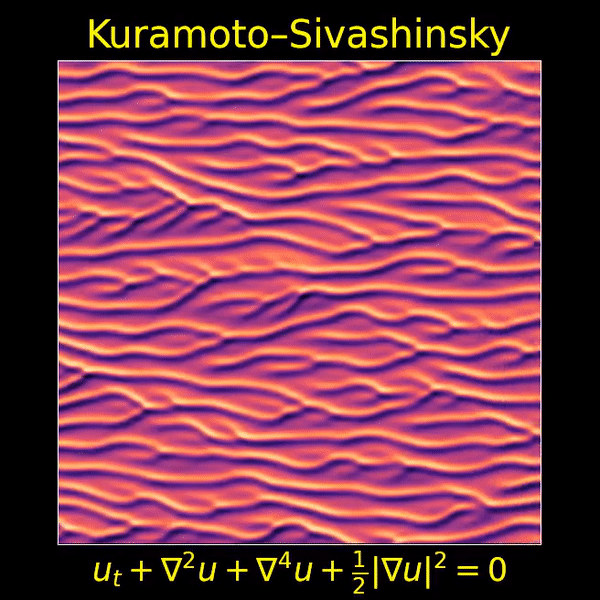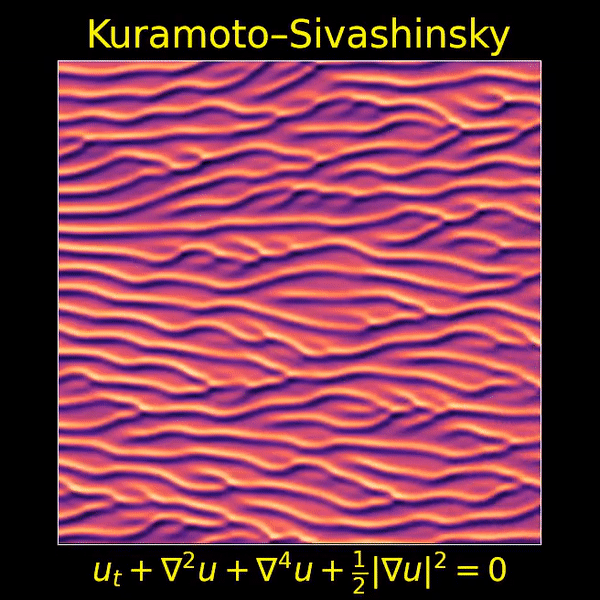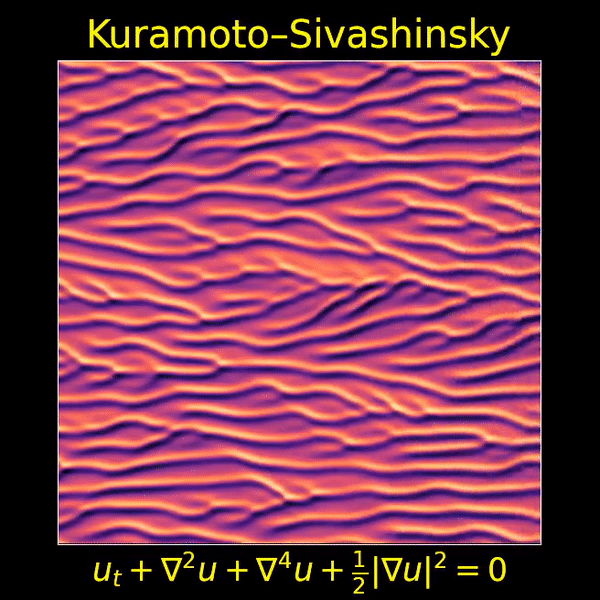

.jpg)
