The Kuramoto–Sivashinsky Equation (Part 2)
Posted by John Baez
I love the Kuramoto–Sivashinsky equation, beautifully depicted here by Thien An, because it’s one of the simplest partial differential equations that displays both chaos and a visible ‘arrow of time’. Now we’ll see that it’s also invariant under ‘Galilean transformations’ — that is, transformations into a moving frame of reference.
Last time I made some conjectures about the Kuramoto–Sivashinsky equation. Most notably, I conjecture that the ‘stripes’ you see above can appear or merge as time passes, but never disappear or split.
But I was quite confused for a while, because the Kuramoto–Sivashinsky equation comes in two forms. The integral form, which I spent most of my time discussing, is this:
where is a real function of two real variables, ‘time’ and ‘space’ . The derivative form is this:
where is again a real function of two real variables. If is a solution of the integral form,
is a solution of the derivative form. This is easy to see: just take the derivative of the equation with in it and see what you get.
By the way, beware of this: Thien An’s wonderful movie above shows the integral form of the equation, but she calls the function
Note that if has a local maximum as a function of then will go positive and then negative. This is important because it affects the definition of ‘stripe’. Here’s what stripes look in the derivative form of the Kuramoto–Sivashinsky equation, as computed by Steve Huntsman:
As you can see, the function goes negative and then positive as we increase moving through a stripe. This means that would have a local minimum.
Another thing puzzling me was that Steve Huntsman found solutions of the derivative form where the stripes in mostly move in the same direction as time passes:
This suggests that there’s some way to take a solution where the stripes aren’t moving much, and switch to a moving frame of reference to get a solution with moving stripes. And indeed I’ll show that’s true! But I’ll also show it’s not true for the integral form of the Kuramoto–Sivashinsky equation — at least not with periodic boundary conditions, which is what we’re using here.
Galilean transformations
Galileo was the guy who first emphasized that the laws of physics look the same in a moving frame of reference, but later Maxwell explained the idea very poetically:
Our whole progress up to this point may be described as a gradual development of the doctrine of relativity of all physical phenomena. Position we must evidently acknowledge to be relative, for we cannot describe the position of a body in any terms which do not express relations. There are no landmarks in space; one portion of space is exactly like every other portion, so that we cannot tell where we are. We are, as it were, on an unruffled sea, without stars, compass, sounding, wind or tide, and we cannot tell in which direction we are going. We have no log which we can case out to take a dead reckoning by; we may compute our rate of motion with respect to the neighboring bodies, but we do not know how these bodies may be moving in space.
All this was before Einstein. Before Einstein came along, a transformation into a moving frame of reference worked like this:
where is a constant, the velocity.
These are called ‘Galilean transformations’ And here’s something cool: the derivative form of the Kuramoto–Sivashinsky equation has Galilean transformations as symmetries! If is a solution, so is the boosted function
The prime here does not mean derivative: is just the name of our new boosted solution. To get this boosted solution, we do the obvious coordinate transformation into a moving frame of reference, but then a bit more: we must subtract the constant
Let’s see how this works! Suppose is a solution of the derivative form of the Kuramoto–Sivashinsky equation:
Then defining
we see the derivative of has an extra term:
while its derivatives are simple:
and so on for the higher derivatives.
This lets us check that the boosted function is also a solution:
Note how subtracting the constant when we transform exactly cancels the extra term term we get when we transform the time derivative of
I got this idea from here:
- Uriel Frisch, Zhensu She and Olivier Thual, Viscoelastic behaviour of cellular solutions to the Kuramoto–Sivashinsky model, Journal of Fluid Mechanics 168 (1986), 221–240.
thanks to someone on Twitter.
Does the integral form of the Kuramoto–Sivashinsky equation also have Galilean transformations as symmetries? Yes, but there’s a certain problem with them. Let’s see how it goes.
If is a solution, then so is this boosted function:
But now the ‘fudge factors’ in the boosted function are more sneaky! We don’t just subtract a constant, as we did with the derivative form. We subtract a function that depends on both the space and time coordinates.
Let’s check. The first time derivative of works like this:
The first space derivative works like this:
The second space derivative is simpler:
and the higher space derivatives work the same way. Now suppose was a solution of the integral form of the Kuramoto–Sivashinsky equation:
We can use our formulas to check that is a solution:
The cancellations in the second step rely crucially on those sneaky fudge factors in the definition of the boosted solution I chose those fudge factors precisely to make these cancellations happen.
Periodic boundary conditions
A lot of really interesting results about the Kuramoto–Sivashinsky equation involve looking at solutions that are periodic in space. For the derivative form this means
It’s easy to see that if obeys this equation, so does its boosted version:
After all, a quick calculation shows
So for any spatially periodic solution with some stripes that are basically standing still, there’s a spatially periodic boosted version where they’re moving at velocity You can think of a spatially periodic solution as a function on the cylinder. In the boosted version, the stripes spiral around this cylinder like the stripes on a barber pole!
But for the integral form this doesn’t work! Suppose is a solution of the integral form that is periodic in space:
Now its boosted version is defined by
and this is not periodic in space:
A conserved quantity
The derivative form of the Kuramoto–Shivashinsky equation has an unexpected symmetry under Galilean transformations, or boosts, even for periodic solutions. It also has an interesting conserved quantity, namely
To see this, note that
Note that if we boost a solution, replacing by we also subtract a constant from this conserved quantity, namely So, it seems that the conserved quantity
is a way of measuring ‘how much the stripes are moving, on average’.
I’ll venture a guess that when
the stripes are stationary, on average. One reason I’m willing to guess this is that this equation has another meaning, too.
I mentioned that we can get solutions of the derivative form from solutions of the integral form by differentiating them, like this:
Does every solution of the derivative form arise this way from a solution of the integral form? Given we can define by
and we can check it obeys the integral form of the Kuramoto–Sivashinsky equation. I’ve been showing you lots of calculations and we’re probably both getting tired of them, so I won’t actually go through this check. But here’s the interesting part. Suppose we restrict attention to spatially periodic solutions! If is spatially periodic, will be so iff
since we have
where in the last step, the first integral is by definition and the second is zero because
and is periodic with period .
Summary
Limiting ourselves to spatially periodic solutions, we see:
The derivative form of the Kuramoto–Sivashinsky equation has symmetry under boosts.
The integral form does not.
Solutions of the integral form correspond precisely to solutions of the derivative form with
- Boosting a solution of the derivative form with
gives a solution where this quantity is not zero.
Given all this, I think the good theorems about spatially periodic solutions of the Kuramoto–Sivashinsky equation will focus on solutions of the integral form, or equivalently solutions of the differential form with
Epilogue: symmetries of the heat equation
At first I was shocked that the Kuramoto–Sivashinsky equation had Galilean transformations as symmetries, because it’s a relative of the heat equation, and the heat equation obviously doesn’t have Galilean transformations as symmetries: you can’t get a solution of the heat equation where a wave of heat moves along at constant velocity as it spreads out.
But then I remembered that the heat equation
is very similar to Schrödinger’s equation:
And Schrödinger’s equation does have Galilean transformations as symmetries, since it describes a free particle! Physicists know how they work. You don’t just replace with you also multiply it by a suitable complex phase that depends on and . That is, you multiply by the exponential of some imaginary-valued function of and
So then I realized that the heat equation does have Galilean symmetries! They work just as for Schrödinger’s equation, but now you have to multiply by the exponential of some real-valued function of and
This grows exponentially as you move in one direction in space, so people thinking about heat often don’t think about such solutions. Yes, you can get a ‘wave of heat that moves along at constant velocity as it spreads out’, but it’s like a huge tsunami wave rolling in from infinity!
I was very proud of myself for having discovered this weird Galilean invariance of the heat equation, and I posed it as a puzzle on Twitter. But then Tom Price pointed out a paper about it:
- U. Niederer, Schrödinger invariant generalized heat equations, Helvetica Physica Acta 51 (1978), 220–239.
It turns out the Galilean invariance of the heat equation, and much more, was discovered by Sophus Lie in 1882!

The so-called ‘Schrödinger group’ also includes certain fractional linear transformations of the plane. So this raises the question of whether the Kuramoto–Sivashinsky equation has even more symmetries than those in the Galilei group (translations, spatial reflections and Galilean transformations).
But it seems this too has been studied:
- Mehdi Nadjafikhah and Fatemeh Ahangari, Lie symmetry analysis of the two-dimensional generalized Kuramoto–Sivashinsky equation, Mathematical Sciences 6 (2012).
This discusses the analogue of the Kuramoto–Sivashinsky equation in two dimensions of space and one of time. It uses some techniques to compute its symmetry group, but I don’t see any sign of invariance under a big group like the ‘Schrödinger group’.

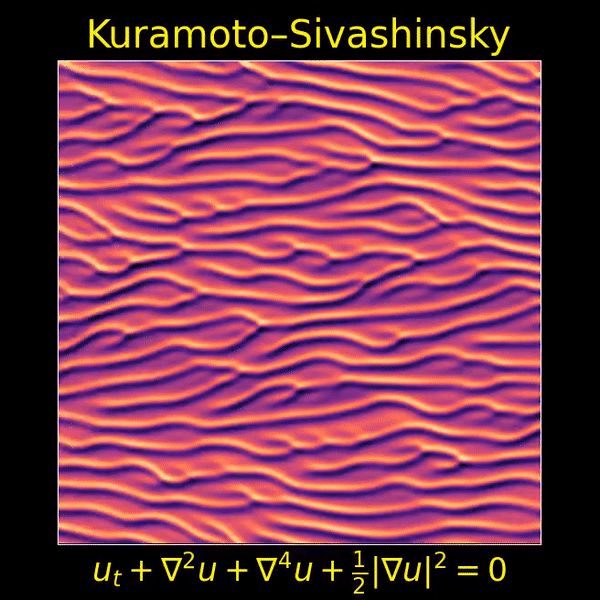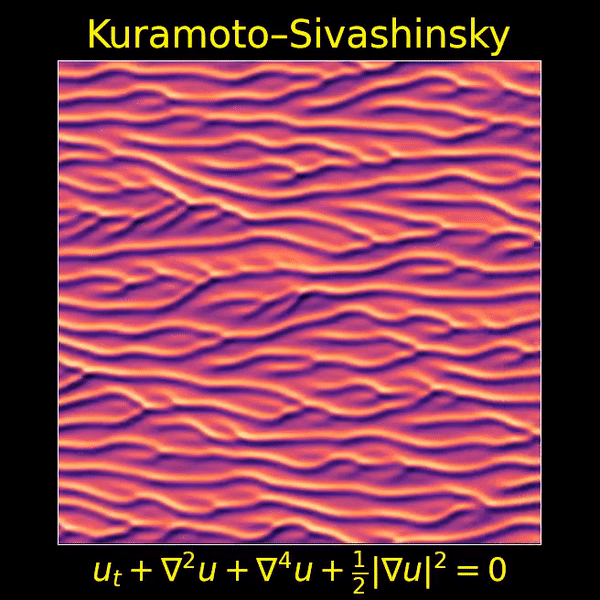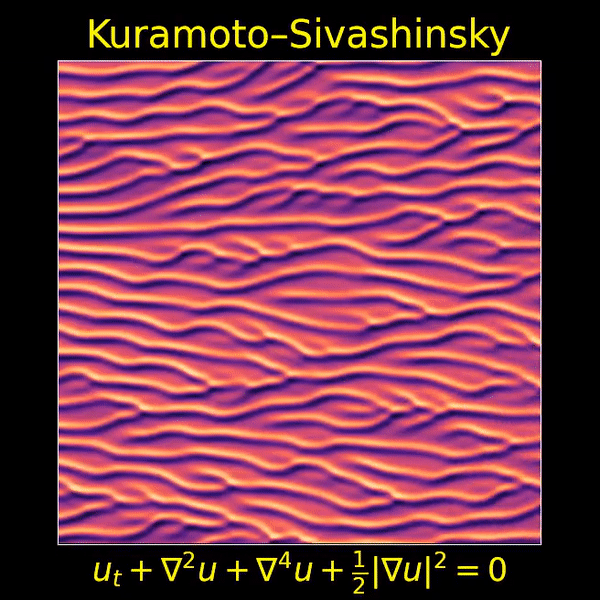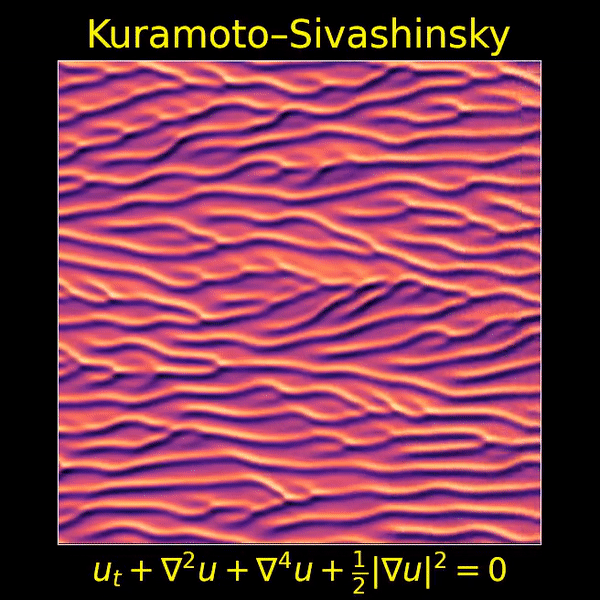


Jared
The heat equation is equivalent to Burgers equation under the Cole Hopf transformation and Burgers enjoys the same Galilean invariance as Kuramoto-Sivashinsky, so that is one way to see it.