K3 Surfaces and the Number 24

January 28, 2022

Posted by John Baez

$MathML-enabled post (click for more details).$

I’m seeking an explicit vector field with exactly 24 zeros, each of index 1, on a K3 surface. This sounds sort of dry and boring, but it’s not! Let me explain.

This post will start out with some gentle exposition, and then lead to an open question that’s been bothering me. If you’re a beginner, start at the beginning. If you’re an expert, maybe start at the end.

$MathML-enabled post (click for more details).$

André Weil named ‘K3 surfaces’ after the mathematicians Kummer, Kähler and Kodaira, but also after the second highest mountain in the world, K2.

This makes them sound remote and forbidding. But let’s climb up to the base camp and get a good view. Then, I’ll ask your help for finding a specific vector field on a specific K3 surface, that may help us see very vividly why the third stable homotopy group of spheres is $\mathbb{Z}/24$ .

K3 surfaces are a certain class of smooth 2-dimensional complex varieties, hence the name ‘surfaces’. But they’re 4-dimensional when viewed as real manifolds. They’re all the same as real manifolds, i.e. diffeomorphic — but they’re not all the same as complex varieties!

The simplest K3 surface, the ‘Fermat quartic surface’, comes from taking the space of nonzero complex solutions of

$w^4 +x^4 +y^4+z^4= 0$

and ‘projectivizing’ it: counting two solutions as the same if they differ by nonzero factor $c$ , like $(w,x,y,z)$ and $(c w,c x,c y,c z)$ .

The Fermat quartic surface lies inside the projective space $\mathbb{C}\mathrm{P}^3$ . In fact any smooth quartic surface in $\mathbb{C}\mathrm{P}^3$ is a K3 surface, so now you have tons of examples.

But what is a K3 surface? I’ll explain it mainly using complex differential geometry, not algebraic geometry: I’m just that kind of guy.

A K3 surface is a simply connected Calabi–Yau manifold of complex dimension 2.

The only other Calabi–Yau manifolds of this dimension are diffeomorphic to a 4-torus $S^1 \times S^1 \times S^1 \times S^1$ , so the phrase ‘simply connected’ is designed to rule out these others, which have a very different flavor.

But what’s a Calabi–Yau manifold? Let me pick one of several equivalent definitions.

A Calabi–Yau manifold is an $n$ -dimensional compact complex manifold for which there exists a nowhere vanishing holomorphic $n$ -form.

Remember, an $n$ -dimensional complex manifold is a manifold where we can locally choose complex coordinates $z_1, \dots, z_n$ , with holomorphic transition functions between different coordinate charts. A holomorphic $n$ -form then looks like

$\omega = f(z_1, \dots, z_n) \, d z^1 \wedge \cdots \wedge d z^n$

where $f$ is a holomorphic function, depending on the chart.

Here’s a fancier way of saying the same thing. Holomorphic $n$ -forms on an $n$ -dimensional complex manifold are sections of a holomorphic line bundle called the canonical bundle. The existence of a nowhere vanishing holomorphic $n$ -form just says this bundle is trivial. So a Calabi–Yau manifold is a compact complex manifold with trivial canonical bundle.

Putting it all together, a K3 surface is a 2d compact complex manifold that’s

Calabi–Yau (its canonical bundle is trivial)

and

simply connected (to rule out tori).

Amazingly, from these bare assumptions people can completely work out the topology of any K3 surface, and ultimately show they are all diffeomorphic!

That takes a lot of work. It’s easier to show their Euler characteristic must be exactly 24. There’s a nice proof in Proposition 1.2.12 here:

Svetlana Makarov, General introduction to K3 surfaces.

I like this because the number 24, my favorite number, comes straight out of the number 12 sitting in the gadget called the ‘Todd class’, defined using the function

$\displaystyle{ \frac{x}{1 - e^{-x}} = 1 + x + \frac{x^2}{12} - \cdots }$

There’s a lot more to say about this, but let’s move on.

Another amazing thing about K3 surfaces is that they’re all hyper-Kähler manifolds. Without getting into the full definition, this implies that besides the usual complex structure on the tangent bundle, which lets us multiply tangent vectors by $i$ , and there are two others, which we’ll call multiplying by $j$ and $k$ , that obey the usual quaternion relations:

$i^2 = j^2 = k^2 = i j k = -1$

Given these two amazing facts we can do something cool. First, the Poincaré–Hopf theorem implies that if a compact manifold has Euler characteristic $k \ge 0$ and you have a smooth vector field on it with only isolated zeros of index $1$ , it must have exactly $k$ of them. Here an ‘isolated zero of index $1$ ’ is a point where in some local coordinates the vector field looks either like this:

$x_1 \frac{\partial}{\partial x_1} + \cdots + x_n \frac{\partial}{\partial x_n}$

or this:

$- x_1 \frac{\partial}{\partial x_1} - \cdots - x_n \frac{\partial}{\partial x_n}$

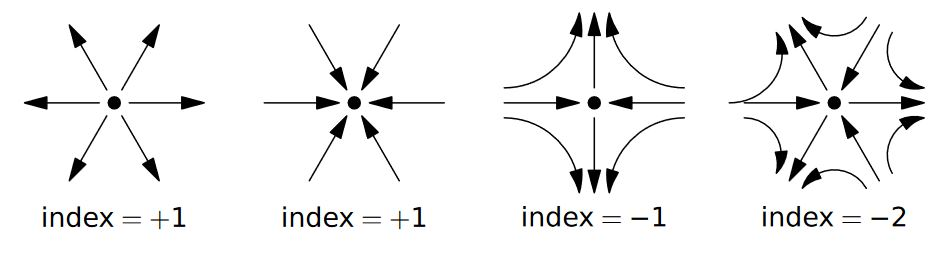
So if a K3 surface has a vector field with only isolated zeros of index $1$ , it must have exactly 24 of them. Less obviously, any K3 surface does have such a vector field!

What I want, though, is an explicit example! David Roberts asked for such an example, but the replies only gave an existence proof:

David Roberts, Vector field on a K3 surface with 24 zeros, MathOverflow.

Why do we care? Here’s why. Take a K3 surface with a vector field $v$ on it with 24 isolated zeros of index $1$ . Remove small open balls around these zeros. The remaining manifold with boundary, say $M$ , is a cobordism from the disjoint union of 24 copies of $S^3$ to the empty set. Furthermore it is a ‘framed’ cobordism, because its tangent bundle has a trivialization (as a smooth vector bundle). Why? Because the vector fields $v, i v, j v$ and $k v$ form a basis of tangent vectors at any point.

Now for the really cool part. Using the connection between stable homotopy theory and framed cobordism theory, it follows that — roughly speaking — the third stable homotopy group of spheres, $\pi_3^S$ , is at most $\mathbb{Z}/24$ !

There are some subtleties here, but they all work out, so skip this paragraph if you want. We need to check that the vector fields $i v, j v, k v$ can be tweaked slightly to be tangent to the 3-spheres that form the boundary of $M$ , and that they then give the ‘standard’ framing of these 3-spheres. We need to notice that a trivialization of the tangent bundle gives a trivialization of the stable normal bundle, which is what really matters for framed cobordism theory. Using the relation between stable homotopy and framed cobordism, our geometric argument then proves that some generator $\nu \in \pi_3^S$ has $24 \nu = 0$ . So all it proves is that if $\pi_3^S$ is a cyclic group generated by $\nu$ , it must either be $\mathbb{Z}/24$ or $\mathbb{Z}/n$ where $n$ divides $24$ . This is what I meant by ‘at most’ $\mathbb{Z}/24$ . Still, our argument gives us some geometrical understanding of how the number $24$ shows up.

For more, see this:

Tilman, answer to Third stable homotopy group of spheres via geometry?, MathOverflow, November 4, 2010.

I want to find a K3 surface with an explicit, nice smooth vector field with exactly 24 zeros, all of index 1.

To do this, it makes sense to find a K3 surface that has the number 24 built into it. It should be very beautiful. And there’s an obvious choice: ‘the tetrahedral Kummer K3’.

Take the 24-cell: the 4-dimensional regular polytope with 24 vertices and 24 faces. You can think of its vertices as a subgroup of the unit quaternions. This group is called the binary tetrahedral group, because it’s a double cover of the rotational symmetry group of the tetrahedron.

The lattice $L$ in the quaternions $\mathbb{H}$ generated by the vertices of the 24-cell is famous: it’s the D₄ lattice (up to a scale factor that doesn’t matter much here). The quotient space $\mathbb{H}/L$ is a 4-torus. Since its a compact complex manifold with trivial tangent bundle it’s a Calabi–Yau manifold! Alas, it’s one of those 2-dimensional Calabi–Yau manifolds that we explicitly ruled out in the definition of K3 surface. But notice that it’s a hyper-Kähler manifold, since its tangent spaces are all canonically isomorphic to the quaternions!

So, we’ve got a 2d Calabi–Yau that’s obviously a hyper-Kähler manifold and deeply connected to the number 24. But it’s not a K3 surface.

Luckily people know how to fix this. First, note that $\mathbb{H}/L$ is an abelian group so for any point $x$ in it there’s a point $-x$ . Thus, we can form the quotient space

$K = \displaystyle{ \frac{\mathbb{H}/L}{x \sim -x} }$

This is a known sort of thing: it’s an example of a Kummer surface. It’s a complex variety, but it’s not smooth at the 16 points coming from points $x \in \mathbb{H}/L$ with $x \sim - x$ . These 16 points are singular, and if we draw just a real 2d surface instead of the full complex 2d surface they look like this:

This is a plaster model of a Kummer surface now at the University of Oxford, designed by Karl Rohn, a student of Felix Klein and Alexander Brill.

It turns out that for any Kummer surface, we can ‘minimally resolve’ its 16 singular points and get a smooth complex variety…. which is a K3 surface!

So, we’ve found a beautiful K3 surface with the number 24 built in from the start. Now you just need to find me a vector field on it with exactly 24 isolated zeros, all of index 1.

If you want to know more about this K3 surface, start here:

Anne Taormina and Katrin Wendland, Symmetry-surfing the moduli space of Kummer K3s.

In Section 1 they discuss the construction of K3 surfaces from Kummer surfaces, which they call Kummer K3s, and they discusses the symmetries of Kummer K3s. The example I just described, called the tetrahedral Kummer K3, is the most symmetrical of them all.

Here’s how its symmetries work. First consider the symmetries of the 4-torus $\mathbb{H}/L$ where $L$ is the D₄ lattice. Remember, this 4-torus is the first step toward building the tetrahedral Kummer K3. Taormin and Wendland call it the tetrahedral torus.

The binary tetrahedral group, called $2T$ , acts both by right and by left multiplication on the quaternions $\mathbb{H}$ . Since these actions commute, the right action preserves the hyper-Kähler structure on $\mathbb{H}$ involving the left action of $i, j$ and $k$ . This right action also preserves the D₄ lattice $L$ , so $2T$ has a right action on the tetrahedral torus $\mathbb{H}/L$ preserving its hyper-Kähler structure. Translations of this 4-torus also preserve the hyper-Kähler structure, and I believe the automorphism group of the tetrahedral torus as a hyper-Kähler manifold is just the semidirect product $2T \ltimes \mathbb{H}/L$ , no more.

The next step toward building the tetrahedral Kummer K3 is to form the Kummer surface

$K = \displaystyle{ \frac{\mathbb{H}/L}{x \sim -x} }$

and the final step is to resolve the singularities in $K$ . These steps interact in a nontrivial way with the symmetries of the tetrahedral torus. For example, the group element $-1$ in $2T$ maps $x \in \mathbb{H}/L$ to $-x$ , so it acts trivially on $K$ . So, the tetrahedral group

$\displaystyle{ T = \frac{2T}{ \{\pm 1\}} }$

acts on $K$ and then on the tetrahedral Kummer K3. This is the group of rotational symmetries of a regular tetrahedron. It’s isomorphic to $A_4$ .

Not all translations of the tetrahedral torus act on the tetrahedral Kummer K3. The quotient process, where we set $x = -x$ , creates 16 singularities in the Kummer surface, coming from points of $\mathbb{H}/L$ that are their own negatives. These points form a subgroup of the $\mathbb{H}/L$ , called its ‘2-torsion subgroup’. We can think of this subgroup as $L/2L$ ; it’s isomorphic to $(\mathbb{Z}/2)^4$ . This subgroup of translations acts on $K$ and then on the tetrahedral Kummer K3.

Putting the pieces together, $T \ltimes L/2L$ acts on the tetrahedral Kummer K3. In fact it acts as diffeomorphisms that preserve the hyper-Kähler structure! Indeed, I’m pretty sure from my readings that the automorphism group of the tetrahedral Kummer K3 as a hyper-Kähler manifold is exactly the semidirect product $T \ltimes L/2L$ , no more. This group is isomorphic to $A_4 \ltimes (\mathbb{Z}/2)^4$ , so it has

$12 \times 16 = 192$

elements.

Note the number 24 is still lurking here, but the 24-element binary tetrahedral group is not acting as symmetries of the tetrahedral Kummer K3. Still, maybe we can use some rather symmetrical construction to build a vector field with 24 zeros of index 1.

This paper gives more details regarding the tetrahedral Kummer K3:

Anne Taormina and Katrin Wendland, The overarching finite symmetry group of Kummer surfaces in the Mathieu group M₂₄.

In particular, Section 4.2 is all about this surface. They also have other papers on this topic.

Please help me out if you can!

Here are some nice pictures of the real parts of a particular Kummer surface, drawn by Abdelaziz Nait Merzouk.

Posted at January 28, 2022 8:43 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/3377

26 Comments & 0 Trackbacks

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

The MathOverflow sidebar just suggested to me the question of whether there exists an octonionic analogue of a K3 surface, which sounds very like something I’d ask if I had been up too late reading about exception-ology.

Posted by: Blake Stacey on January 29, 2022 9:00 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Thanks for pointing that out! The answer is yes, it exists: that is, an 8-dimensional manifold that demonstrates the 7th stable homotopy group of sphere is ‘at most’ $\mathbb{Z}/240$ . However, it sounds quite complicated to me. In the quaternionic case I’m talking about here — finding a 4-dimensional manifold that demonstrates the 3rd stable homotopy group of spheres is ‘at most’ $\mathbb{Z}/24$ — we know any K3 surface will do the job (they’re all diffeomorphic), and we know lots of beautiful constructions of these, but we don’t yet know an explicit construction of a suitable vector field. We don’t know an explicit construction of one in the octonionic case either, but the quaternionic case seems a lot easier!

Posted by: John Baez on January 30, 2022 3:30 AM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Can there exist such a vector field which is holomorphic?

Posted by: Tim Campion on January 30, 2022 10:39 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Or even quaternionic-analytic?

Posted by: Tim Campion on January 30, 2022 10:40 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

To clarify – I mean, if we relax the “explicitness” criterion, does there exist a holomorphic vector field on a K3 surface with 24 zeros, all of index 1? Knowing the answer to that question might help focus the search for an explicit example.

Posted by: Tim Campion on January 30, 2022 10:45 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Oh, I see this was answered in the negative on David’s MO post.

Posted by: Tim Campion on January 30, 2022 10:53 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

I haven’t even thought about whether the Poincaré–Hopf theorem works for complex vector fields! This would be good to know. But I was just imagining a good old real vector field, smooth and maybe real-analytic but not complex-analytic.

The MathOverflow comment suggesting that

not complex-analytic $\implies$ not ‘explicit’

seems wrong to me.

Posted by: John Baez on January 30, 2022 11:24 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

The “explicit” version of this that I’d like to see is something that you could encode in homotopy.io along the lines of what Andre did here for the sphere eversion. But this can be a little bit complicated because you usually want to construct elements in smaller unstable homotopy. That is, Andre actually constructs the generator of infinite order in $\pi_7(S^4)$ , which stabilizes to the generator of order 24 in $\pi_8(S^5)$ .

In other words, I’d like some kind of “embedded normally framed Morse decomposition” where you write the Pontryagin-Thom framed manifold in terms of handles which are easy to intepret as morphisms in an $\infty$ -groupoid with an n-loop. An explicit formula for the K3 surface minus the 24 spheres in homotopy.io is a proof of the relation the generator (coming from stabilizing Andre’s generator) satisfies in $\pi_8(S^5)$ .

An interesting variation on this K3 question is my MO question. Here I want a similar formula for why the generator of $\pi_5(S^2)$ when you stabilize it into $\pi_8(S^5)$ becomes the element of order 12.

The simplest question along these lines which I do not know the answer to, is an explicit formula for the generator of $\pi_6(S^3)$ . This shouldn’t be too bad because it’s in the image of the unstable(!) J-homomorphism, but I still don’t know how to make it explicit enough to put in homotopy.io

(Let me apologize in advance for the inevitable typo somewhere above.)

Posted by: Noah Snyder on January 31, 2022 12:20 AM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

I’ve seen an explicit map $S^6\to Sp(1)$ before that is the generator, given by a quaternionic formula. Would this help, or is that not what you meant?

Posted by: David Roberts on January 31, 2022 9:09 AM | Permalink | Reply to this

Jason

$MathML-enabled post (click for more details).$

As noted by others, the only holomorphic vector field is the zero vector field. So every description will be at least somewhat “non-holomorphic”. I find a useful description to be the one in terms of an elliptic fibration over the complex projective line (the Riemann sphere) rather than in terms of the blowing up of the involution quotient of a complex torus. The holomorphic, proper map from the K3 surface to the complex projective line has precisely 24 critical points, and these will be the points where the “almost holomorphic” vector field vanishes. Choose small closed balls around each of these points. On the open complement, the holomorphic tangent bundle surjects to the pullback of the holomorphic tangent bundle of the complex projective line, and the kernel is the dual of this pullback. As a complex vector bundle with a smooth structure, this short exact sequence splits. Just as the Hirzebruch surface $F_4$ is diffeomorphic to the Hirzebruch surface $F_0$ , also this split direct sum of holomorphic line bundles is smoothly equivalent to a direct sum of two trivial holomorphic line bundles. Thus there exists an everywhere nonzero global section on the complement of the 24 balls. Finally, the restriction of this section to the boundary of each ball is equivalent to a self-map of the 3-sphere in the homotopy class of the identity map. As a section of a trivial rank 2 complex vector bundle on the boundary of the ball, this extends (by scaling) to a smooth section that vanishes precisely at the center of the ball.

Posted by: Jason Starr on January 31, 2022 6:31 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

If I recall correctly, a differentiable manifold is orientable when it has a nowhere vanishing top form.

Now you’ve defined a Calabi-Yau manifold as a compact complex manifold with a nowhere vanishing holomorphic top form.

Can we interpret a nowhere vanishing holomorphic top form as orientability in the complex context?

If so, we could say a Calabi-Yau manifold is a compact orientable manifold in the complex context.

I have a vague suspicion that complex orientability is already used to mean something else though.

Posted by: Mozibur Ullah on January 31, 2022 10:17 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

There’s definitely an analogy between orientable manifolds and Calabi–Yau manifolds. In the former, a nonzero section of the $n$ th exterior power of the cotangent bundle of a real $n$ -manifold reduces the structure group of the tangent bundle from $GL(n,\mathbb{R})$ to $SL(n,\mathbb{R})$ . In the latter, a nonzero holomorphic section of the $n$ th exterior power of the cotangent bundle of a complex $n$ -manifold reduces the structure group of the tangent bundle from $GL(n,\mathbb{C})$ to $SL(n,\mathbb{C})$ . But in the latter case people often start with a Kähler manifold, where the structure group is $\mathrm{U}(n)$ . Then making it Calabi–Yau reduces the structure group to $SU(n)$ .

There’s also a spooky difference between the two cases, because a complex $n$ -manifold has dimension $2n$ as a real manifold, so while we can’t find holomorphic $p$ -forms on it with $p \, >\, n$ , it has $p$ -forms with $p$ up to $2n$ . So, calling a holomorphic $n$ -form on a complex manifold a ‘top form’ feels odd to me.

Posted by: John Baez on February 1, 2022 12:56 AM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Great, it’s nice to see an analogy working out.

I’m not sure I understood your ‘spooky’ point. I said a holomorphic top form and not just top form. That is, in the former we use complex dimension and in the latter real dimension. So $n_\mathbb{C}$ in the former is $2n_\mathbb{R}$ in the latter. (The subscripts indicate complex or real dimension).

However, if I said top form in a complex context, I mean a holomorphic top form. But this is most likely my idiosyncratic use of mathematical language.

Posted by: Mozibur Ullah on February 1, 2022 9:30 AM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

I’ve never heard anyone say ‘holomorphic top form’, perhaps because ‘holomorphic’ here would be changing the meaning of ‘top’: it’s not just a top form that happens to be holomorphic. But if anyone does say holomorphic top form, I won’t argue with them; I’m getting too old to spend much time in arguments about terminology.

To me the ‘spookiness’ is not about terminology; maybe I didn’t make that clear. What’s spooky is how a complex $n$ -manifold resembles a real $n$ -manifold in some ways and a real $2n$ -manifold in others, and we need to keep both these things in mind. This is very well-known, but it’s still peculiar.

Posted by: John Baez on February 1, 2022 4:32 PM | Permalink | Reply to this

Spooky manifolds

$MathML-enabled post (click for more details).$

Ok, that is spooky!

Posted by: Mozibur Ullah on February 1, 2022 5:47 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Among other sources, that analogy is developed in Richard Thomas’s contribution to the Roger Penrose birthday volume.

Posted by: Jason Starr on February 1, 2022 1:26 AM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Using that analogy, Donaldson-Thomas invariants of Calabi-Yau threefolds are analogues of the Casson invariant of three-manifolds.

Posted by: Jason Starr on February 1, 2022 1:33 AM | Permalink | Reply to this

Mozibur

$MathML-enabled post (click for more details).$

Is that the analogy that Richard Thomas developed?

I’ve heard of both invariants but know little about them (and I mean little in the conventional sense and not in the mathematical sense = I know a lot but I could know more and I’m gonna hedge just in case someone turns up knowing a lot more! - and someone always does, especially on the net) so having this analogy makes it easier to understand.

I just looked up the definition of Casson invariant on Wikipedia. It looked scary at first glance but then I saw it wasn’t as scary as I first thought. It’s developed in three parts from orientated:

a. Integral homology 3-spheres

b. Rational homology 3-spheres

c. Closed 3-manifolds

Nlab just mentions the first and second. To define the first, they begin by considering SU(2)-valued reps of the fundamental group of the 3-manifold under question.

What are these? I know what an ordinary rep of a group is but I don’t think I’ve come across group valued reps before.

Then nlab says the Casson invariant counts equivalence classes in their moduli space. They also call these SU(2)-local systems which sounds like a term in algebraic geometry.

They also point out that the Donaldson-Thomas invariants are used to count BPS states in string theory. It’s nice to see a connection to physics, even if I only vaguely understand what both terms mean.

There’s a further connection to physics on the Wikipedia page - or at least to gauge theory. Apparently Taubes showed that the Casson invariant on a homology 3-sphere M is the Euler characteristic of A/G where A is the space of SU(2) connections over M and G is the group of gauge transformations.

Are there Casson invariants for higher homology spheres? Presumably not, otherwise presumably at least one of Nlab and Wikipedia would have mentioned them.

Posted by: Mozibur Ullah on February 1, 2022 10:13 AM | Permalink | Reply to this

Re: Mozibur

$MathML-enabled post (click for more details).$

I double-checked, and actually the article is by both Simon Donaldson and Richard Thomas. Sorry for leaving out one of the authors!

Posted by: Jason Starr on February 1, 2022 2:27 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Mozibur wrote:

To define the first, they begin by considering SU(2)-valued reps of the fundamental group of the 3-manifold under question.

What are these? I know what an ordinary rep of a group is but I don’t think I’ve come across group valued reps before.

“SU(2)-valued representation of the fundamental group” is just an idiosyncratic way of talking about a homomorphism from the fundamental group to SU(2).

I see your subject header came out looking like “Mozibur”.
Since this subject header problem is happening mainly to people who post to the $n$ -Category Café for the first time, it’s probably related to that. I suggest looking at the “Subject” entry while you are posting a comment. You can edit it, so make sure it doesn’t have anything in it you don’t want. (I just made mine say “Re: K3 Surfaces and the Number 24” instead of “Re: Mozibur”.)

Posted by: John Baez on February 1, 2022 4:40 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Posted by: Jason Starr on February 3, 2022 11:46 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Jason wrote:

As noted by others, the only holomorphic vector field is the zero vector field. So every description will be at least somewhat “non-holomorphic”. I find a useful description to be the one in terms of an elliptic fibration over the complex projective line (the Riemann sphere) rather than in terms of the blowing up of the involution quotient of a complex torus. The holomorphic, proper map from the K3 surface to the complex projective line has precisely 24 critical points, and these will be the points where the “almost holomorphic” vector field vanishes.

This is great! Thanks a million!

It took me a while to understand this since I’m just a beginner in algebraic geometry. I needed to learn a bit about elliptic K3 surfaces. For anyone else in my situation, I recommend this review:

Daniel Huybrechts, Lectures on K3 surfaces, Chapter 11: Elliptic K3 surfaces.

He defines an elliptic K3 surface to be a K3 surface $X$ together with an elliptic fibration: a surjective morphism $\pi \colon X \to \mathbb{P}^1$ such that the geometric generic fibre is a smooth integral curve of genus one or, equivalently, if there exists a closed point $t \in \mathbb{P}^1$ such that $X_t = \pi^{-1}(t)$ is a smooth integral curve of genus one.

This is a bit too algebraio-geometric for my taste; it would be nice to have an equivalent definition over $\mathbb{C}$ phrased in the language of complex geometry, if that’s possible.. but I think I get the point.

Huybrechts says that generically K3 surfaces do not admit an elliptic fibration, but those that do generically have all but 24 fibers $X_t$ being smooth genus-1 curves, with the 24 singular fibers being rational curves with a single double point.

So that’s where the 24 comes from!

Now I would like to get my hands on some concrete examples of K3 surfaces having an elliptic fibration with 24 singular fibers, so I can study all of this explicitly.

Choose small closed balls around each of these points. On the open complement, the holomorphic tangent bundle surjects to the pullback of the holomorphic tangent bundle of the complex projective line, and the kernel is the dual of this pullback. As a complex vector bundle with a smooth structure, this short exact sequence splits. […] this split direct sum of holomorphic line bundles is smoothly equivalent to a direct sum of two trivial holomorphic line bundles. Thus there exists an everywhere nonzero global section on the complement of the 24 balls.

Great! I would like to explicitly get ahold of such a nonzero vector field in a concrete example. (Noah wants to make all this stuff concrete to give a computerized constructive proof of this result, but my reason is slightly different: I suspect that there’s a very beautiful example, and I want to see it.)

Finally, the restriction of this section to the boundary of each ball is equivalent to a self-map of the 3-sphere in the homotopy class of the identity map. As a section of a trivial rank 2 complex vector bundle on the boundary of the ball, this extends (by scaling) to a smooth section that vanishes precisely at the center of the ball.

Nice! I guess this construction provides a vector field on our K3 that is not smooth on the boundary of each ball. Of course it can be smoothed. But that doesn’t really interest me: what really matters, for the construction of the framed cobordism, is the behavior of the vector field outside the open balls that we’re removing from the K3. And here, if I understand correctly, you are promising us it will be not just smooth but holomorphic! Very nice.

Posted by: John Baez on February 3, 2022 11:47 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

Seeking an explicit example, I posted the following question on MathOverflow:

For me a K3 surface will be a smooth complex projective variety of dimension 2 that is simply-connected and has trivial canonical bundle. Given a K3 surface $X$ , an elliptic fibration $\pi \colon X \to \mathbb{C}P^1$ is a proper morphism with connected fibers such that all but finitely many fibers are smooth curves of genus 1. I’ve learned a little about these from here:

Daniel Huybrechts, Lectures on K3 surfaces, Chapter 11: Elliptic K3 surfaces.

Generically a K3 surface admits no elliptic fibration, but among those that do, generically the fiber of $\pi$ is a smooth curve of genus 1 at all but 24 points, where the fiber is a rational curve with a single double point.

Huybrecht also catalogues the less generic cases where $\pi$ has fewer singular (i.e. non-smooth) fibers, but with correspondingly worse singularities. On MathOverflow there’s a nice easy example: the Fermat quartic surface admits an elliptic fibration with 6 singular fibers, each of which has 4 double points.

But I’d like to see concrete easy examples of elliptic fibrations with 24 singular fibers.

By ‘concrete easy examples’ I mean that ideally I would like there to be simple explicit formulas for the K3 surface $X$ , the hyper-Kähler structure on $X$ , the elliptic fibration $\pi$ , the 24 points on $\mathbb{C}\mathrm{P}^1$ with singular fibers, the double points on these fibers, and also the points of $X$ where $d\pi$ is not injective. But of course I’ll settle for whatever I can get!

Will Sawin answered:

Weierstrass equations are probably a good choice. You can try $y^2 = x^3 - 3x +2 t^{12},$ for example.

Here the singular fibers are when $t$ is a $24$ th root of unity $\zeta$ , and the double point is provided by $x = \zeta^{12}$ and $y=0$ .

Aren’t the points where $d\pi$ is not injective the same as the singular points?

To really describe this as a smooth surface over $\mathbb{P}^1$ , first note that we can get a surface in $\mathbb{P}^2 \times \mathbb{A}^1$ by homogenizing, i.e. taking $(x:y:z)$ to be the coordinates of $\mathbb{P}^2$ and $t$ the coordinate of $\mathbb{A}^1$ , look at the vanishing locus of the equation $y^2 z= x^3 - 3x z^2 +2 t^{12}z^3$ and then another chart is provided by changing variables to $\tilde{x} = x/ t^4$ , $\tilde{y} = y/t^6$ , $\tilde{z} = z$ , $\tilde{t} =1/t$ , where after the change of variables we are looking at the vanishing locus of the equation $\tilde{y}^2 \tilde{z} = \tilde{x}^3 - 3 \tilde{t}^8 \tilde{x} \tilde{z}^2 +2 \tilde{z}^3$ in $\mathbb{P}^2 \times \mathbb{A}^1$ with coordinates $(\tilde{x}:\tilde{y}:\tilde{z}),\tilde{t}$ .

For me a hyper-Kähler structure is just a nowhere vanishing holmorphic 2-form. Such a 2-form is provided here by $\frac{d x}{y} \wedge d t = \frac{d (t^4 \tilde{x} )}{t^6\tilde{y} } \wedge d t = \frac{t^4}{t^6} \frac{d\tilde{x}}{\tilde{y}} \wedge d t = - \frac{d\tilde{x}}{\tilde{y}}\wedge d \tilde{t}.$

I answered:

“Aren’t the points where dπ is not injective the same as the singular points?” I was suffering from some bad mental image where they looked different. But if a fiber of π has a double point, locally shaped like a letter X, the map dπ must vanish in two directions at that point, not just one, so it has lower rank there. (“Injective” was never really an option I guess.)

Then Will pointed out another issue:

It’s subtle, but Jason Starr’s construction of a vector field is not actually holomorphic on the complement (as you claimed on the bottom of the linked thread). If it were, it would imply a global holomorphic vector field by Hartog’s theorem. There are two non-holomorphic steps — splitting an exact sequence over the complement and a Hirzebruch-like isomorphism between two complex vector bundles on $\mathbb{P}^1$ . The second one I know how to do with explicit formulas, but I don’t know how to do the first one.

Posted by: John Baez on February 4, 2022 12:03 AM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

192 stuck in my mind from its cameo appearance in https://oeis.org/A001676 amidst sporadic appearances of 24.

Posted by: Tom Copeland on February 4, 2022 5:22 AM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

When I hear the number “192”, I think of how

$192 + 56 = 248$

is the dimension of $\mathrm{E}_8$ … somehow this decomposition shows up when you think about $\mathrm{E}_7$ sitting in $\mathrm{E}_8$ .

But trying to remember this, I bumped into something else, namely that the Weyl group of $\mathrm{D}_4$ has 192 elements. Since I described a K3 surface built from the $\mathrm{D}_4$ lattice that has 192 symmetries as a hyper-Kähler manifold, it’s natural to hope that this symmetry group is secretly the $\mathrm{D}_4$ Weyl group. But I don’t actually see how that could be, since it’s $\mathrm{A}_4 \ltimes (\mathbb{Z}/2)^4$ , and I don’t think the $\mathrm{D}_4$ Weyl group is isomorphic to that.

(I could be wrong.)

Posted by: John Baez on February 4, 2022 6:08 PM | Permalink | Reply to this

Re: K3 Surfaces and the Number 24

$MathML-enabled post (click for more details).$

I think the $\mathrm{D}_4$ Weyl group is $(\mathbb{Z}/2 \ltimes \mathrm{A}_4) \ltimes (\mathbb{Z}/2)^3$ , rather than $\mathrm{A}_4 \ltimes (\mathbb{Z}/2)^4$ ; see Eq. (28) of Koca et al. (2003). I could very well be missing something important, though.

Posted by: Blake Stacey on February 7, 2022 3:33 AM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

January 28, 2022