The n-Category Café

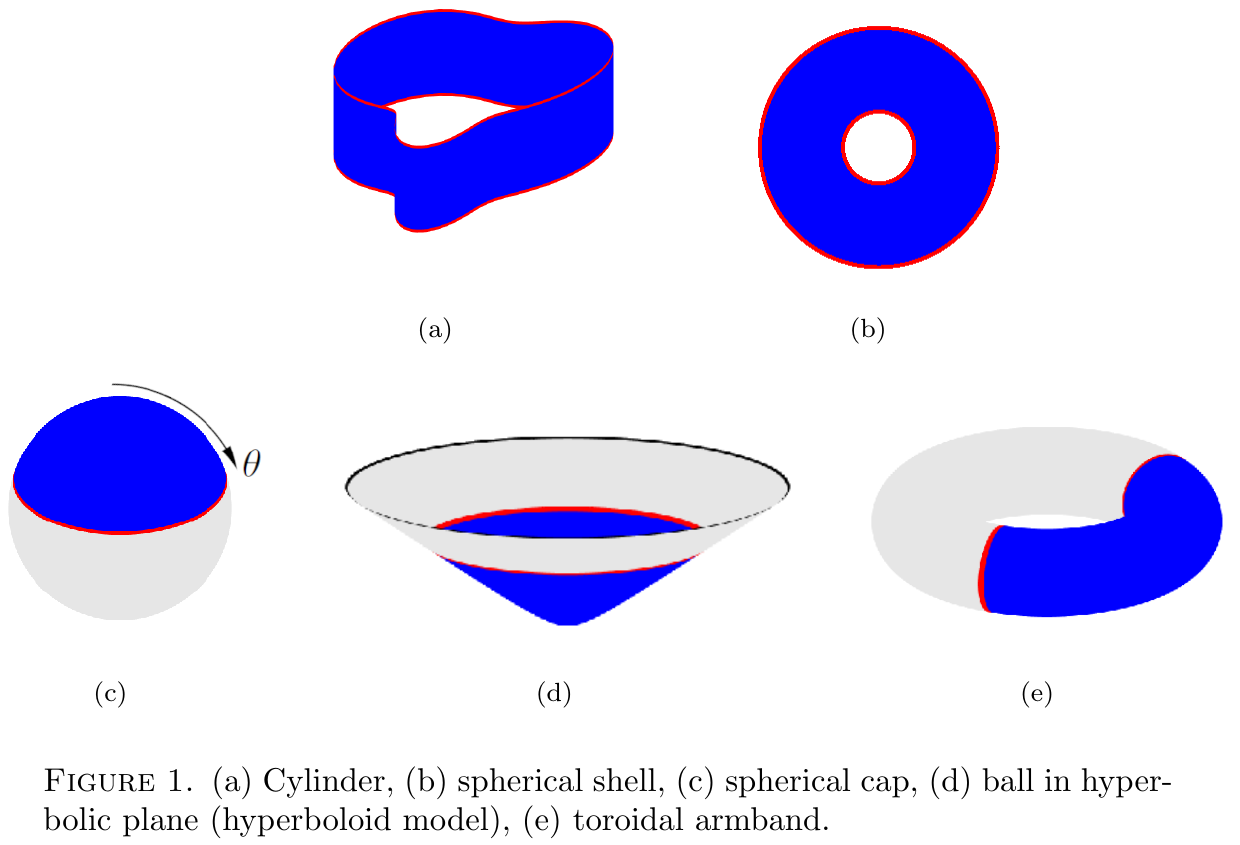
Recent years have seen much progress to understand the geometric content of the magnitude function for domains in odd-dimensional Euclidean space. In this setting Meckes and Barceló–Carbery showed how to compute magnitude using differential equations. Nevertheless, as Carbery often emphasized, hardly anything was known even for such simple geometries as the unit disk $B_2$ in $\mathbb{R}^2$.

Our new works Semiclassical analysis of a nonlocal boundary value problem related to magnitude and The magnitude and spectral geometry show, in particular, that as $R\to \infty$,

$$\mathcal{M}_{B_2}(R) = \frac{1}{2}R^2 + \frac{3}{2}R + \frac{9}{8}+O(R^{-1}),$$

and that $\mathcal{M}_{B_2}(R)$ is not a polynomial.
The approach does not use differential equations, but methods for integral equations. Recall that the magnitude of a positive definite compact metric space $(X,\mathrm{d})$ is defined as

$$\mathcal{M}_{(X,D)}(R):=\int_X u_R(x) \ \mathrm{d}x,$$

where $u_R$ is the unique distribution supported in $X$ that solves the integral equation

$$\int_X \mathrm{e}^{-R\mathrm{d}(x,y)}u_R(y) \ \mathrm{d}y=1.$$

We analyze this integral equation in geometric settings, for domains $X$ in $\mathbb{R}^n$, in spheres, tori or, generally, a manifold with boundary with a distance function of any dimension, as illustrated in the figures above. Our results shed light on the geometric content of their magnitude. In fact, our results apply beyond classical geometry and metric spaces — not even a distance function is needed!

Our techniques suggest a life of magnitude beyond metric spaces in information geometry. There one considers a statistical manifold, i.e. a smooth manifold $X$ with a divergence $D$, not with a distance function: See John Baez’s posts on information geometry. A first example of a divergence is the square of the subspace distance $|x-y|^2$ on a submanifold in Euclidean space. A second example is the square of the geodesic distance function on a Riemannian manifold $(X,g)$, provided that it is smooth. (Note that on a circle the distance function and its square are non-smooth when $x$ and $y$ are conjugate points.) In general, a divergence $D=D(x,y)$ is a smooth, non-negative function such that $D$ is a Riemannian metric near $x=y$ modulo lower order terms, in the sense that

$$D(x,x+v)=g_{D,x}(v,v)+O(|v|^3)$$

for a Riemannian metric $g_D$ on $X$.

Divergences related to relative entropy have long been used in statistics to study families of probability measures. The relative entropy of two probability measures $\mu$ and $\nu$ on a space $\Omega$ is defined as

$$D(\mu,\nu):=\int_\Omega \log\left(\frac{\mathrm{d}\nu}{\mathrm{d}\mu}\right)\mathrm{d}\nu\in [0,\infty].$$

The notion of relative entropy and its cousins are discussed in the blog posts of Baez mentioned above and also in Leinster’s book Entropy and Diversity: The Axiomatic Approach. While the space of probability measures is too big, one can restrict to interesting submanifolds (with boundary).

Here is the definition of the magnitude function of a statistical manifold with boundary $(X,D)$, when $R \gg 0$ is sufficiently large:

$$\mathcal{M}_{(X,D)}(R):=\int_X u_R(x) \ \mathrm{d}x,$$

where $u_R$ is the unique distribution supported in $X$ that solves the integral equation

$$\int_X \mathrm{e}^{-R\sqrt{D(x,y)}}u_R(y) \ \mathrm{d}y=1.$$

When $D$ is the square of a distance function on $X$, we recover the magnitude of the metric space $(X,\sqrt{D})$.

We emphasize two key points to take home:

1. The integral equation approach is equivalent to defining the magnitude of statistical manifolds using Meckes’s classical approach in Magnitude, diversity, capacities, and dimensions of metric spaces, relying on reproducing kernel Hilbert spaces.

2. Since $D$ is smooth, $\mathcal{M}_{(X,D)}$ shares the properties stated in The magnitude and spectral geometry for the magnitude function summarized next.

Theorem

a. The magnitude is well-defined for $R\gg 0$ sufficiently large; there the integral equation admits a unique distributional solution.

b. $\mathcal{M}_{(X,D)}$ extends meromorphically to the complex plane.

c. The asymptotic behavior of $\mathcal{M}_{(X,D)}(R) = \frac{1}{n! \omega_n} \sum_{j=0}^\infty c_j(X) R^{n-j}+O(R^{-\infty})$ is determined by the Taylor coefficients of $v\mapsto D(x,x+v)$ and $n=\mathrm{dim} X$.

Further details and explicit computations of the first few terms $c_j$(X) can be found in The magnitude and spectral geometry: For a Riemannian manifold $c_0$ is proportional to the volume of $X$, while $c_1$ is proportional to the surface area of $\partial X$. $c_2$ involves the integral of the scalar curvature of $X$ and the integral of the mean curvature of $\partial X$. All these computations are relative to $D$ and the Riemannian metric that $D$ defines. For Euclidean domains $X \subset \mathbb{R}^n$, $c_3$ is proportional to the Willmore energy of $\partial X$ (proven with older technology in another paper: The Willmore energy and the magnitude of Euclidean domains). We note that

in all known computations of asymptotics for Euclidean domains $X \subset \mathbb{R}^n$, $c_j(X)$ is proportional to $\int_{\partial X}H^{j-1}\mathrm{d}S$ for $j\gt 0$.

Here $H$ denotes the mean curvature of $\partial X$. You can compute lower-order terms by an iterative scheme, for as long as you have the time. In fact, we have written a python code which computes $c_j$ for any $j$, which is available at arXiv:2201.11363.

We would love to hear from you should you have any thoughts on the following questions:

• Is magnitude an interesting invariant for information geometry?

• Is there a category theoretic motivation, like Lawvere’s view of a metric space as an enriched category?

• Does the magnitude relate to notions studied in information geometry?

• Do you have interesting questions about this invariant?