Amplimorphisms
Posted by Urs Schreiber
In some parts of the quantum field theory literature, that concerned with algebraic formulations, one finds the concept of an amplimorphism of algebras.
For a -algebra and a vector space ( some field), people call an algebra homomorphism of the form an amplimorphism.
Without actually admitting it, people are talking about an entire 2-category of such amplimorphisms. (Update: the 2-category of amplimorphisms is made explicit in section 2.1 of P. Zito’s thesis.)
All this is done – “old school” – in components (as far as I am aware), which makes it a little hard to see what amplimorphisms really are.
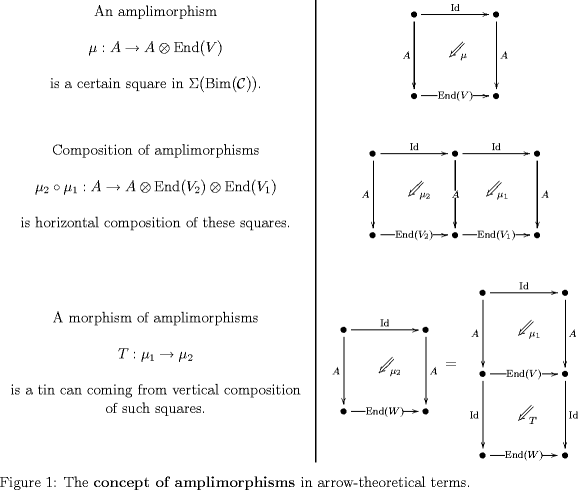
After thinking about it for a while, it seems I found that the 2-category of amplimorphisms is a certain natural 2-category of rectangles internal to the 3-category – the 1-object 3-category obtained from the monoidal 2-category of algebras and bimodules over .
This is described here:
Does anyone here know anything about amplimorphisms? And how best to think about them? What they really are?
The term was apparently first used in
K. Szlachanyi, K. Vecsernyes,
Quantum symmetry and braid group statistics in -spin models
Commun. Math. Phys. 156, 127-168 (1993)
(pdf)
To quickly see the definition, go to the beginning of
G. Mack, V. Schomerus
Models of Quantum Space Time: Quantum Field Planes
hep-th/9403170
For lots of further details check out section 3 of
Florian Nill, Kornel Szlachanyi
Quantum Chains of Hopf Algebras with Quantum Double Cosymmetry
hep-th/9509100.
Some hints concerning the use of amplimorphisms in the study of symmetries of (rational conformal) field theories can be found here:
J. Fuchs, A. Ganchev, P. Vecsernyes
On the quantum symmetry of rational field theories
hep-th/9407013
Update: Feb 6, 2007
The point of introducing amplimorphisms originally, was that people were looking for a braided category of representations of some Hopf algebra, which would be equivalent to the category of representations of local observable algebras in 2-dimensional QFT (compare the next entry).
It seems that K. Szlachanyi and K. Vecsernyes somehow just guessed this concept. And it apparently took a while to demonstrate that it does indeed yield the desired equivalence.
In
Peter Vecsernyés
On the Quantum Symmetry of the Chiral Ising Model
hep-th/9306118
we can see the author intoduce the concept of an amplimorphism. As a motivation, he writes (on p. 3)
[in order to get nontrivial braiding] we are to study algebra embeddings of type, that is amplifying monomorphisms of , where is an matrix with entries in , in order to mimic the endomorphisms of the observables.
I cannot yet quite follow this motivation. In which sense does this “mimic endomorphisms”?
Later, on p. 8, we are told that
[…] we will use amplifying monomorphisms, or amplimorphisms, for short, of instead of representations. The benefit of this choice stems from the existence of a left inverse of an amplimorphism, which can lead to the notion of conditional expectations, statistics parameter and index.
Finally, the thesis mentioned above is
Pasquale A. Zito
2--Categories with non-simple units
On p. 13, P. Zito makes one important aspect of amplifunctors explicit (p. 13):
for infinite-dimensional algebras for which the notion of amplimorphisms reduces to that of ordinary endomorphisms. Hence we can understand amplimorphisms as a way to obtain certain features of infinite-dimensional algebras already for finite-dimensional algebras.

Re: Amplimorphisms
I’ll admit this is the first time I’ve heard of the concept, but the first thing that leaps out at me is the top line of your diagram.
I think some insight can come from writing this a little differently.
Now looks like it’s “intertwining” the two endomorphism algebras, and looks like the intertwinor morphism. Whether this is obvious, useless, or interesting I don’t know offhand.