Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

February 1, 2007

Towards the FFRS Description of 2dCFT (B)

Posted by Urs Schreiber

More of our little seminar preparing us for the description of 2-dimensional conformal field theory in terms of “state sum models” internal to modular tensor categories.

Last time we had understood how to build representations of 2-dimensional cobordisms (called “2-dimensional quantum field theories”) by chopping these up into generators: the pair of pants, the cap, the co-pair of pants and the co-cap.

As we move up in dimension, and as we put extra structure on our cobordisms, it will become increasingly hard to find and handle a collection of such generators.

But: it will always be easy to chop any 2-dimensional cobordism into “2-generators”: little disk-shaped 2-dimensional pieces of our cobordism.

So we need to think about how to think about 2-processes that occur over such “2-generators”.

After doing, so, we rediscover the Frobenius property as an incarnation of the exchange law of 2-processes and see why we want to triangulate our cobordism and color the triangulation with a Frobenius algebra.

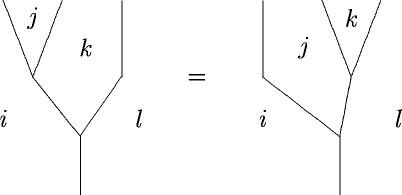
Part 2: colored triangulations and adjunctions

Secretly, this is all about expressing one 2-functor – one on the entire cobordism, say – in terms of another one # – living only over a little piece of cobordism.

This is possible if both are connected by a special ambidextrous adjunction: something weaker than an equivalence but stronger than an adjunction.

And special ambidextrous adjunctions are precisely what gives rise to special Frobenius monads.

And if we want to glue what we had sliced before, we need special Frobenius monads in ribbon categories.

And this is why we see special Frobenius algebras internal to ribbon categories decorating triangulations of surfaces.

The glue and the ribbon will appear in the next set of notes.

Posted at February 1, 2007 5:45 PM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1140



3 Comments & 1 Trackback

Re: Towards the FFRS Description of 2dCFT (B)

The glue and the ribbon will appear in the next set of notes.

I did run badly out of time with preparing this. But here are some rough notes, for the moment:

glue and trace

Posted by: urs on February 1, 2007 9:19 PM | Permalink | Reply to this

Re: Towards the FFRS Description of 2dCFT (B)

A pair of pants is, Morse-wise, a disc orientably glued to an anulus along a thickend 0-sphere piece of its boundary and containing a (+−)(+-)-critical point, while a cap is a disk glued along a 1-sphere piece of its boundary (so it has to be the whole boundary) containing a (++)(++)- or (−−)(--)-critical point, etc; and the Morse theory in more dimensions gives strongly analogous pictures for cutting up cobordisms generally, partially gluing in n-disks along boundary portions S k−1×B n−kS^{k-1}\times B^{n-k}…

And I can see there can easily be complications in more dimensions—maybe recognising when a boundary-embedded S k−1S^{k-1} has boundary neigborhood a trivial bundle, transition maps across the gluing being very twisty, etc— But if it’s not too digressive, can someone point at or explain why focussing on “the” Morse cells in a cobordism might NOT be the right approach for more dimensions?

Posted by: In Anonymity on February 2, 2007 3:43 AM | Permalink | Reply to this

generators

might NOT be the right approach for more dimensions?

I think one problem is that there is no good understanding of diffeomorphism classes of closed manifolds for higher dimensions. Then it is difficult to show that the generators and relations you would obtain by some method (like the one you have in mind) are sufficient.

For 3-dimensional cobordisms one makes use of the fact that every closed 3-manifold can be obtained from the 3-sphere by surgery. This is at the heart of the Reshitikhin-Turaev description of 3-dimensional TFT by means of modular categories.

But already for 4-dimensional manifolds there is nothing much known at all, as far as I am aware.

Posted by: urs on February 2, 2007 11:13 AM | Permalink | Reply to this
Read the post Amplimorphisms and Quantum Symmetry, I
Weblog: The n-Category Café
Excerpt: Localized endomorphisms of quantum observables in arrow-theoretic terms.
Tracked: February 6, 2007 12:06 PM

Post a New Comment