Supercategories
Posted by Urs Schreiber
Motivated by general questions in supersymmetric QFT, I would like to better understand some of the “arrow-theory” behind supersymmetry, finding a formulation which gives a systematic way to internalize the concept into various contexts. For instance, people have a pretty good purely arrow-theoretic understanding of finite-group QFT, such as Dijkgraaf-Witten theory. Can we understand how to superize this systematically, in a context where many of the standard tools one finds in the literature are simply not applicable?
In order to both motivate and further introduce the problem, I might, in a followup entry, start looking into the following
Exercise (The Willertonesque super 2-particle). Simon Willerton has demonstrated (see The Baby Version of Freed-Hopkins-Teleman) that the “quantum theory of the 2-particle propagating on a finite group” has a beautiful arrow-theoretic formulation:
Take the parameter space of the 2-particle to be the fundamental groupoid of the circle Take its target space to be a finite group Then configuration space is the groupoid which plays the role of the loop group of the finite group . The fact that this 2-particle is charged gives rise to a 2-vector bundle on this configuration space, and quantum states of the 2-particle are sections of this. In the simplest case (see the above entry for the more general case), this simply means that a state here is a representation of the configuration space groupoid on vector spaces.
There is more structure here, but for the moment concentrate on this basic data. The point of this is that everything is purely combinatorial, well defined, and exhibits just the bare structure of the QFT here, stripped of all distracting technicalities.
The exercise is then: do the analogous discussion for the super 2-particle. Figure out what the super-parameter space of the super 2-particle in the above sense is, what its super-configuration space supergroupoid is and what its super-representations on supervector space are like.
Clearly the first step to make any progress at all here is to get a reasonable good understanding what supersymmetry really is, such as to apply it to this situation. So, this entry here is just about this question: What is the arrow theory of supersymmetry?
As an attempt to approach this exercise, I’ll introduce the concept of a supercategory, which is supposed to be to that of a supergroup like categories are to groups. I feel that this concept helps extracting some of essence of what is going on.
It turns out that this is closely related to another structure which has appeared in 2-dimensional QFT, that of G-equivariant categories.
It’s an exercise. I can’t be sure that I am on the right track. But I would like to share the following, as I proceed.
In the pdf
I give the following definition, and try to indicate why I think it is useful.
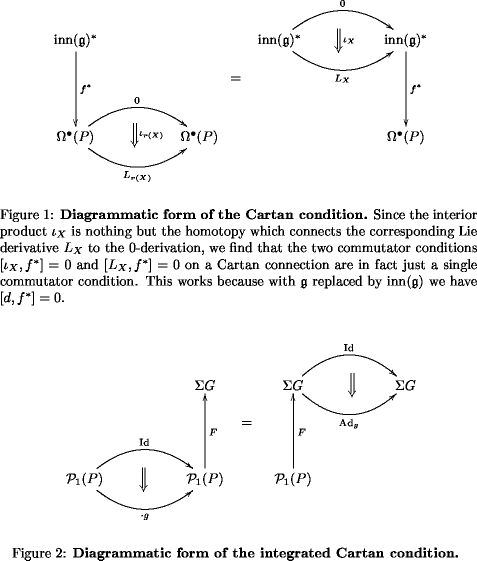
Definition. A super category is a diagram in such that
Personally, I find it helpful to think of as the “flow of a (odd) vector field” on , using the philosophy of What is a Lie derivative really?
Definition. Given a supercategory , a grading and a grading operator on is a subcategory preserved by , together with a nontrivial transformation the “fermion number operator” (think ) such that is central and involutive with respect to the horizontal composition of natural transformations.
Here is to be thought of as the subcategory of which contains exactly the grading-preserving morphisms.
In the usual QFT applications, we expect to see monoidal supercategories, which are braided for QFTs in dimensions two or higher and symmetrically braided in dimension three or higher. The notion of braided monoidal supercategories naturally leads over to the -equivariant fusion categories considered by Turaev and Kirillov.
In
-equivariant monoidal categories
there is an attempt to understand the structure here as a generalization of the concept of -tuply stablized -categories:
an ordinary braided monoidal category is the same as a one-object, one-morphism 3-category. What, in this sense, is a braided monoidal supercategory?
It seems to be the answer is this:
like an ordinary braided monoidal catgeory is a 3-category which in lowest degrees looks like the trivial 2-group, a braided monoidal supercategory is a 3-category which in lowest degree looks like the strict 2-group that comes from the crossed module I am calling this generalization of stabilization of -categories currently -stabilization. So the claim would be that braided monoidal supercategories come from -stabilized 3-categories, with the above strict 2-group.
Indepently of its appearance here in the context of supersymmetry, I would very much enjoy to hear any comments on this generalized notion of stabilization. Has it been considered anywhere?

Re: Supercategories
What confuses me here is that you envisage supercategories as generalizing supergroups. I don’t know what a supergroup is , but it doesn’t seem that a supercategory generalizes one. A supercategory is “a thing”, and not “a collection of things”… this is weird.
, but it doesn’t seem that a supercategory generalizes one. A supercategory is “a thing”, and not “a collection of things”… this is weird.