The n-Category Café

I am very glad that David Roberts joined me on the quest for inner peace – I mean: for inner automorphisms. I very much enjoyed this fruitful exchange. All by email, of course, and intercontinental, as befits a true blog community.

David has a bunch more notes on how everything and more works in the world of simplicial groups, making in particular the relations to Brano Jurčo’s work Crossed Module Bundle Gerbes; Classification, String Group and Differential Geometry more manifest.

We are grateful to Jim Stasheff for accompanying this capital $\mathrm{INN}(G_{(n)})$ endeavour with his guidance, and for making us relate it, by the mapping cone construction, more closely to the lower case $\mathrm{inn}(g_{(n)})$ business, which we have been involved in recently.

Related entries:

I started thinking about $\mathrm{INN}(G_{(2)})$ in my first entry titled $n$-Curvature. There the point was that we can understand the differential 2-cocycles given by Breen and Messing as morphisms $$I \stackrel{\mathrm{tra}}{\to} \mathrm{curv}$$ of 3-functors, where $$\mathrm{curv} : P_3(X) \to \Sigma \mathrm{INN}(G_{(2)})$$ plays the role of the 3-curvature of the pseudo transport 2-functor $\mathrm{tra}$, following the general mechanism described in Sections, States, Twists and Holography.

The trivializability of $\mathrm{INN}(G_{(2)})$ is crucial here: it makes $\mathrm{curv}$ a flat 3-transport, which is the Bianchi identity in this context, as described in the second entry called $n$-Curvature as well as in Curvature, the Atiyah Sequence and Inner Automorphisms.

But this relation to 3-curvature is not mentioned in the present text. In fact, at the moment I am not completely sure how it relates conceptually to the fact – which we do discuss – that $\mathrm{INN}(G_{(2)})$ plays the role of the universel $G_{(2)}$-2-bundle. It feels a litte embarrassing, since there ought to be an obvious relation. But at the moment it escapes me.

$\Sigma(\mathrm{INN}(G_{(2)}))$-3-transport is supposed to give the right notion of parallel transport in particular for spinning strings, being the integrated version of the 3-connections discussed in terms of Lie $n$-algebras in Connections on String-2-Bundles, following the general mechanism described in Chern Lie (2n+1)-algebras.

(But notice that there seem to be also much more mundane applications: in The $n$-Café quantum conjecture I indicated how ordinary $U(1)$-bundles with connection can be conceived in terms of $\mathrm{INN}(\mathbb{Z} \to \mathbb{R})$-transport, thereby making the appearance of “phases” (i.e. elements in $U(1)$) a phenomenon emerging from more ordinary ingredienty like the integers and the reals. )

In fact, the realization described in Derivation Lie 1-Algebras of Lie $n$-Algebras that the Lie $(n+1)$-algebra $$\mathrm{inn}(g_{(n)})$$ of inner derivations of any Lie $n$-algebra $g_{(n)}$ arises as the mapping cone of the identity on $g_{(n)}$ motivated David Roberts and myself, greatly influenced by Jim Stasheff’s guidance, to pursue what is now advertized as one of the two main results of our text: that $\mathrm{INN}(G_{(2)})$ is indeed the nonabelian mapping cone, in the sense of Conduché, of the identity on $G_{(2)}$.

Finally, on a more speculative note, it seems remarkable that the construction of short exact sequences of Lie $(2n+1)$-algebras for every transgressive Lie $(2n+1)$-cocycle is very much controlled by the exact sequence $$\mathrm{Disc}(G) \to \mathrm{INN}(G) \to \Sigma G$$ of groupoids, for $G$ any Lie (1-)group, which plays the role of the universal $G$-bundle.

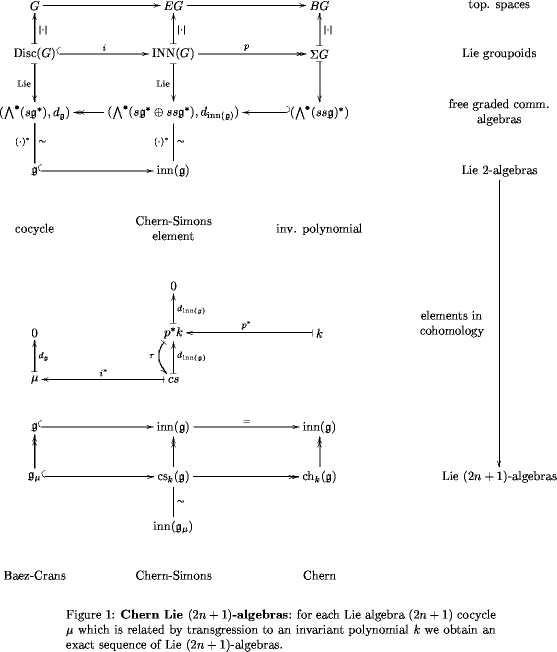
This makes one naturally wonder if this entire construction has a counterpart when we replace the sequence $\mathrm{Disc}(G) \to \mathrm{INN}(G) \to \Sigma G$ by the sequence $$\mathrm{Disc}(G_{(2)}) \to \mathrm{INN}(G_{(2)}) \to \Sigma G_{(2)}$$ for $G_{(2)}$ any strict Lie 2-group, which plays the role of the universal $G_{(2)}$-2-bundle.

This should involve something like a categorification of the concept of a Lie algebra cocycle, namely a Lie 2-algebra cocycle, as well as the related notions of transgression and invariant polynomials.

I have the vague suspicion that this is what will finally allow to put the supergravity Lie 3-algebra in its proper home, using the fact that the Poincaré Lie algebra, which the supergravity Lie 3-algebra is an extension of, being a semidirect sum, really wants to be regarded as a strict Lie 2-algebra. But this I still haven’t figured out yet.