Local Nets from 2-Transport

December 9, 2007

Posted by Urs Schreiber

$MathML-enabled post (click for more details).$

While listening to AQFT talks last Friday I further developed the thoughts that I started talking about in

Oberwolfach CFT, Arrival Night, Algebra of Observables and Sheaves of Observables.

I wrote up a note in which the passage from $n$ -dimensional functorial QFT to the corresponding AQFT local net of observables is described in more detail:

On nets of local operators from 2-transport

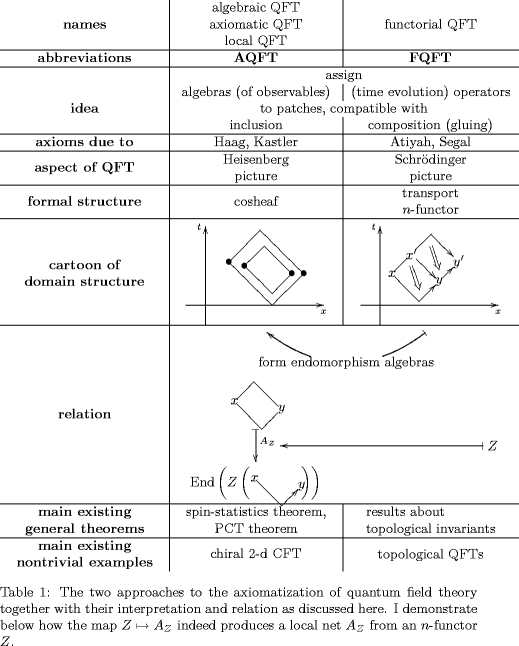
Abstract. I would like to understand how the axioms of a local net of observable algebras follow from those of a transport $n$ -functor with values in $n$ -vector spaces. I suggest that local nets of algebras result when applying to an $n$ -vector transport a categorified version of the transition from the Schrödinger to the Heisenberg picture of quantum mechanics.

Here I consider some simple aspects of this question for $n=2$ . I show that every extended 2-dimensional QFT gives rise to a net of local monoids on 2-dimensional Minkowski space. The construction has an obvious generalization to arbitrary $n$ .

$MathML-enabled post (click for more details).$

Introduction.

Nets of operator algebras (you can find details for a 1-dimensional net, which is slightly different from what I am considering here, discussed in the entry CFT in Oberwolfach, Monday morning) are functors from subcategories of open subsets of pseudo-Riemannian spaces to a poset of subalgebras of some ambient algebra, usually that of bounded operators on some Hilbert space.

Using the pseudo-Riemannian structure, one singles out those pairs of subsets which are spacelike separated. A net of operators is called local if the subalgebras assigned to spacelike separated subsets commute with each other.

Nets of local operator algebras have been introduced in order to formalize the concept of the algebra of observables in quantum field theory.

Out of the study of these structures a large subfield of mathematical physics has developed, which is equivalently addressed as algebraic quantum field theory, or as axiomatic quantum field theory or as local quantum field theory, but usually abbreviated as AQFT.

To my mind, all three of these terms as such would equally well describe also what is probably the main alternative parallel development, as endeavours towards giving quantum field theory a good axiomatic framework: the study of representations of cobordism categories.

While this approach did apparently not receive a canonical name so far, I am used to referring to it as \emph{functorial quantum field theory}. Here I shall abbreviate that as FQFT.

An obvious question is: What is the precise relation between AQFT and FQFT? I am not aware of any explicit attempt to answer this. To a large extent, developments in AQFT and FQFT have been, in the past, rather disconnected.

The most successful – strikingly successful – application of AQFT has actually been to chiral 2-dimensional conformal field theory. Here AQFT has provided a rich collection of results, notably important classification results. (On the other hand it is still unclear, as far as I am aware, how to realize the main motivating example, 4-dimensional gauge theory of Yang-Mills type, in the language of AQFT.)

The most well known application of FQFT is to topological quantum field theory (TQFT): the theory of representations of categories of cobordisms up to diffeomorphism. This goes so far that some people have expressed the believe that FQFT = TQFT instead of FQFT $\supset$ TQFT. While this is actually not the case – since whenever we have a category of cobordisms with extra structure (conformal, Riemannian) the notion of FQFT on it makes sense – it is true that the tractability of FQFT away from the topological realm drops sharply.

But progress is visible. The closest possible point of contact between AQFT and FQFT obtained so far is possible the description of full 2-dimensional conformal field theory in terms of a topological QFT internal to the representation category of a chiral net, as given by Fuchs, Runkel and Schweigert (FRS).

As indicated in Towards 2-functorial CFT how at least parts of the topological aspect of the FRS description arises from a “local trivialization” of an $(n=3)$ extended FQFT transport 3-functor. The discussion to follow can be regarded as providing also the connection between this $n$ -functor and the chiral nets. But many details remain to be better understood.

In any case, it is clear that both AQFT and FQFT are relevant for understanding what quantum field theory really is. Since there is just one reality, there should be a way to relate them systematically.

Here I shall try to present evidence which suggests that the situation is as indicated by the following slogan:

AQFT is to FQFT like the Heisenberg picture of quantum mechanics is to the Schrödinger picture. Forming endomorphism algebras provides a systematic map from FQFT to AQFT.

For this to work, it is important to understand FQFT as what is sometimes called extended functorial QFT: originally FQFT was conceived as being about functors from cobordisms categories to some category of vector spaces. But later it was realized that, more generally, one wants to model extended cobordsisms, which live in higher categories. Hence an extended $n$ -dimensional functorial quantum field theory is an $n$ -functor.

Posted at December 9, 2007 4:51 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1530

17 Comments & 3 Trackbacks

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

This is very interesting Urs. I’d like to know : how restrictive is it that you are using diamond shaped regions instead of more general open sets?

Also, you define the FQFT as a 2-functor from the path 2-category to Vect. However the path 2-category only contains lightlike paths. Can you do it for the “full” path 2-category? I guess it should be the one which only contains timelike paths.

Posted by: Bruce Bartlett on December 10, 2007 10:49 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

how restrictive is it that you are using diamond shaped regions instead of more general open sets?

I think one would reduce the discussion of arbitrary subsets to those causal ones: each arbitrary subset has the smallest causal set that it sits inside. So we assign to an arbitrary set the algebra corresponding to that smallest causal subset, I think.

This is related to the time-slice axiom, which is usuallay demanded of a local net when one is working with arbitrary subsets:

if $O_1 \subset O_2$ and $O_1$ contains a Cauchy surface of $O_2$ , then the algebras already coincide, $A(O_1) = A(O_2)$ .

(Hopefully some AQFT expert chimes in to correct what needs correction here.)

you define the FQFT as a 2-functor from the path 2-category to Vect

Well, not quite. One would have to consider a 2-functor to 2Vect, eventually, with some suitable notion of 2Vect. Possibly one factoring through the bicategory of von-Neumann algebras, bimodules and bimodule homomorphisms.

For toy examples very remote from “reality” we might consider 2-functors to $\mathbf{B}Vect$ : the one-object 2-category with a single object $\bullet$ and $End(\bullet) = Vect$ .

(This would make best sense if we also discretized the domain, such that $Obj(P_2(X)) = \mathbb{Z}^2$ , in which case, I think, actually a reasonably interesting toy example would be obtained.)

In any case, the 2-functor $Z$ would assign to paths something that looks more or less like a vector space, yes. This we think of as the vector space of states on that path.

But in my notes I wanted to evade that issue entirely, concentrating just on the structure underlying the situation. For that reason I didn’t actually make any assumption on the codomain 2-category at all, and merely derived a “local net of monoids”, namely the endomorphism monoids of the values of $Z$ on paths.

In real-life examples these monoids should actually be algebras with plenty of extra structure (C^*, von Neumann, factors,…)

Can you do it for the “full” path 2-category? I guess it should be the one which only contains timelike paths.

I think the central conclusion which I presented, namely that the 2-functoriality of $Z$ alone induces the axioms of a local net on the collection of the endomorphism algebras of its values on paths is pretty robust as far as the nature of the 1-morphisms is concerned. But the 2-morphisms need to know about the causality structure somehow, lest there is no chance they can induce the locality axiom.

Clearly there are plenty of things that would need to be done now. The points you mention belong to them. Also the equivariance under the Poincaré group action needs to be incorporated. And ultimately probably the general situation described on p. 6-7 in The generally covariant locality principle.

Have to run now. Lunch :-)

Posted by: Urs Schreiber on December 10, 2007 12:00 PM | Permalink | Reply to this

Re: Local Nets from 2-Transport

Mmm… diamonds :)

Posted by: Eric on December 11, 2007 3:38 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

Mmm… diamonds :)

Indeed.

I know there is something at our fingertips. It is big. And beautiful. But it is dark, I still cannot entirely see it.

But I keep groping.

Posted by: Urs Schreiber on December 11, 2007 1:29 PM | Permalink | Reply to this

Re: Local Nets from 2-Transport

But I keep groping.

I have faith in you :)

The discussion on “tovariance” is very interesting and you can sense the interconnections closing in on each other. Very fun to watch. For some reason, “tovariance” reminds me of an itching feeling I always had that there was some kind of duality (if that is the right word) between continuum theories and discrete theories and your comments made me wonder if that duality (or whatever the right word is) could be related to a choice of “topos”. I never grocked what “topos” was all about, but the term kept coming up all over the place in things I always felt were interrelated, e.g. NCG, synthetic geometry, discrete geometry, etc. It seems the “truth” is “arrow theory”, something that I’m still sadly not anywhere closer to understanding.

Keep up the fight! :)

Posted by: Eric on December 12, 2007 3:50 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

some kind of duality (if that is the right word) between continuum theories and discrete theories and your comments made me wonder if that duality (or whatever the right word is) could be related to a choice of “topos”.

Yes! Or: essentially yes!

You wouldn’t want to call it a duality unless passing back and forth gets you back where you started. Usually this will not be the case. But it might be the case.

And, I think, the choice, in general, is some choice of context. Whether we demand that context to have the properties of a topos will depend on some details.

Up to these details, what you just said is pretty much what I said in the entry The Principle of General Tovariance and in particular in this comment. There I said

for a big chunk of physics, we want at least three things:

a) an object in our ambient category which plays the role of parameter space

b) another object in our ambient category which plays the role of target space

c) the internal hom object between these two objects: the space of fields.

There are a couple of different ambient categories – some of them happening to be topoi (but all of them playing a different role compared to the topoi that for instance Döring and Isham consider) – that have immediate practical relevance:

a) we might interpret the above in the context of categories internal to finite sets. This is the right choice for instance if we want to describe finite group field theory, as in Simons’s published and Bruce-and-Simon’s unpublished work.

b) we might interpret the above in the world of $\infty$ -groupoids internal to either Top or sheaves on manifolds or the like. This would be the right choice for more sophisticated applications than finite group field theory. Most everything ever considered in physics should live here.

c) essentially equivalently but more tractable, we don’t internalize to Lie ∞-groupoids but to their Lie $\infty$ -algebroids. Most everything ever considered in QFT has actually (more or less secretly) been spelled out here.

I think it is important not to confuse internalization in a topos with internalization in general.

All of the machinery of a physical theory should be internal to some context. The backend of the physical theory, namely that part which “interfaces with reality”, the part where we determine how to extract propositions about the physical system under study, that part should not be just internal to an arbitrary context, but to a topos. Simply because a topos is precisely the sort of context in which the notion of a proposition makes sense.

Together with John Baez, I therefore formulated a principle which I am thinking of, in all modesty, as a refinement and improvement over the proposed “principle of general tovariance”:

Principle: When formulating geometry and physics, follow the principle of concept and context (formalize internally, as much as possible). When you reach the point where you want to address the measurement problem of quantum mechanics, make sure that the context has the properties of a topos, in order to be able to extract the logic of observations predicted by the model.

Posted by: Urs Schreiber on December 12, 2007 11:08 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

the “truth” is “arrow theory”, something that I’m still sadly not anywhere closer to understanding.

It’s just a fancy word for the basic idea of math: abstraction.

Given some concept that works well, you step back and analyze what it is that makes it work. To which degree does it depend on the context you are working in, to which degree is it independent of that.

Then you say: whenever the context has these and those properties, my concept here makes sense in that context.

I keep giving that extremely simple but important example from physics:

in the study of systems that arise as “sigma-models” (including pretty much every fundamental system that you can think of, but not including weird non-fundamental things like the kicked top or the like) the concept is this:

you have a thing, usually thought of as a “space”, and called parameter space

you have another thing called target space

you then want to form the thing of maps from parameter space to target space (and call that the space of fields).

The point here is: with parameter space and target space being things of sorts, also the collection of maps between them needs to be such a thing.

So this concept “sigma-model” makes sense whenever the context which we interpret it in satisfies the requirement that

in this context the collection of maps from one thing to another is itself a thing.

Such contexts are very well known. They are called closed categories.

So, the concept of a sigma-model (at least the simplified version of this concept that I am discussing here) makes sense in every closed category.

For continuum physics one would usually take this context to be the category of sheaves on manifolds, or something like that, which is a closed category of “smooth spaces” in which the collection of maps from one smooth space to another smooth space is itself a smooth space.

(And, incidentally, the category of sheaves on manifolds happens to be a topos. But this seems to be a “coincidence” of sorts. It is not the crucial property of a topos that we are making use of here (the existence of a subobject classifier $\Omega$ ), but the closedness of the category.)

For discrete physics one would use another context. The category of simplicial sets, maybe, or of cubical sets (though, I must admit, I am not sure if cubical sets form a closed category). Maybe vaguely: the category of “discrete spaces”, whichever way you want to model that.

If you ensure that this category is closed, in that the collections of morphisms from one “discrete space” to another forms itself a discrete space, then you can interpret the concept “sigma model” in that context.

That’s a (simple) example for what I’d call “arrow theory”. And what saner people call “internalization”.

Posted by: Urs Schreiber on December 12, 2007 11:29 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

Eric wrote:

It seems the “truth” is “arrow theory”, something that I’m still sadly not anywhere closer to understanding.

Someday someone should write a clear, simple explanation of what Urs is doing. But maybe we should wait until Urs ‘succeeds’ in some widely agreed-upon sense. Right now his cauldron is bubbling and brewing, spitting out lots of good math… but I’m not sure the meal is cooked yet.

Urs wrote:

I must admit, I am not sure if cubical sets form a closed category.

They should. In fact, as long as your cubical sets are just functors $f: C^{op} \to Set$ for some category $C$ , you’re bound to get a topos of cubical sets. After all, $hom(C^{op},Set)$ is always a topos, and a topos is always cartesian closed.

Marco Grandis and Luca Mauri investigate 3 choices for $C$ . which give three somewhat different definitions of cubical sets:

Marco Grandis and Luca Mauri, Cubical sets and their site.

The idea is that the objects of $C$ are cubes, one for each dimension $n = 0,1,2, \dots$ . The morphisms should include ‘face inclusions’ (inclusions of cubes in higher-dimensional ones) and ‘degeneracies’ (ways of squashing down cubes to a lower-dimensional ones). That way, any cubical set

$F : C^{op} \to Set$

will have a set of $n$ -cubes $F(n)$ for each $n$ , and each $n$ -cube will have a bunch of lower-dimensional faces and a bunch of higher-dimensional ‘degeneracies’.

You may be more comfy with simplicial sets, which use a different choice of $C$ . But, the abstract nonsense is very similar, including the fact that we get a topos.

Grandis and Lauri also consider the option of adding extra morphisms to $C$ . But if only include faces and degeneracies, $C$ is what Grandis and Mauri call the restricted cubical site. They describe it in 5 equivalent ways!

The most obvious description is this. Think of the $n$ -cube as the set of its corners. A corner of the $n$ -cube is just an $n$ -tuple of bits (0’s and 1’s). So, the $n$ -cube is just the set $2^n$ , consisting of all $n$ -tuples of bits.

The allowed morphisms $f: 2^n \to 2^m$ are just functions that delete some bits in our $n$ -tuple and insert some new bits, without changing the order of the bits we started with.

For example, the four obvious face inclusions from the 1-cube to the 2-cube are these functions $f: 2^1 \to 2^2$ :

$0 \mapsto 00 , 1 \mapsto 10$ $0 \mapsto 01, 1 \mapsto 11$ $0 \mapsto 00, 1 \mapsto 01$ $0 \mapsto 10 , 1 \mapsto 11$

There are some mind-boggling beautiful abstract descriptions, too!

Posted by: John Baez on December 13, 2007 1:30 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

Urs wrote: “I must admit, I am not sure if cubical sets form a closed category.”

They should. In fact, as long as your cubical sets are just functors $f: C^{op} \to Set$ for some category $C$ , you’re bound to get a topos of cubical sets. After all, $hom(C^{op}, Set)$ is always a topos, and a topos is always cartesian closed.

That’s true of course, but there is more than one option for the monoidal structure. In particular, for at least one flavor of cubical sets that I know of, let’s say “vanilla”, the site $C$ of cubes carries a monoidal structure which may roughly be described as the “walking monoidal category with an interval”.

Here, the “interval” is an object $x$ equipped with two endpoints

$d_0, d_1: I \to x$

where $I$ is the monoidal unit, and a common retraction $s: x \to I$ of these endpoints (so $s \circ d_0 = 1_I = s \circ d_1$ ). The site of cubes is the initial monoidal category equipped with such structure. (For this flavor of cube, there are no symmetries or connections.)

The presheaf category $Set^{C^{op}}$ carries a Day convolution product induced from the monoidal product on $C$ , and in answer to Urs, this monoidal category is biclosed. This is a general feature of Day convolution on presheaf categories generated from a monoidal site; it therefore holds just as well for the more exotic flavor of monoidal cubical site that Grandis and Mauri consider.

Posted by: Todd Trimble on December 13, 2007 2:43 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

Todd wrote:

That’s true of course, but there is more than one option for the monoidal structure. In particular, for at least one flavor of cubical sets that I know of, let’s say “vanilla”, the site $C$ of cubes carries a monoidal structure which may roughly be described as the “walking monoidal category with an interval”.

Good point.

I’d never looked hard at Grandis and Mauri’s paper until I wrote the comment you just replied to. But, your “vanilla” cubical site $C$ is what they call the “restricted cubical site”. And, among their 5 descriptions of this category, there were these:

“the free strict monoidal category with an assigned internal bipointed object”

and

“the classifying category of the monoidal theory of bipointed objects”

which remind me a lot of what you’re saying.

Posted by: John Baez on December 13, 2007 6:07 PM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

Right now his cauldron is bubbling and brewing, spitting out lots of good math… but I’m not sure the meal is cooked yet.

Certainly not. Also, it’s not a small elephant I would like to see cooked.

It was quite a while ago that I started thinking about how extended functorial QFT should be connected to AQFT, and the main idea was clear early on: it’s about what “Schrödinger picture” and “Heisenberg picture” and their transition really means.

But it took hearing that AQFT talk last week to finally trigger the materialization of the explicit construction, which I presented here.

(And it’s quite nice, isn’t it: explicitly relating the concept of “locality” in AQFT to $n$ -functoriality and the exchange law, as it should be.)

Posted by: Urs Schreiber on December 13, 2007 11:38 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

I never grocked what “topos” was all about

Actually, it’s a very simple idea formulated in very scary words.

It’s just about the “arrow theory”, i.e. the abstract concept of a characteristic function, which is a concept that is, literally, taught in elementary school.

Namely, a subset $S \subset K$ of a bigger set $K$ is uniquely given by its characteristic function $\chi_{S} : K \to \{0,1\}$ $\chi_S : k \mapsto \left\lbrace \array{ 1 & if k \in S \\ 0 & otherwise } \right. \,.$

This is so very obvious and trivial, that most people wouldn’t spend much time thinking about it.

But those who followed Arnold Ross’s motto to think deeply about simple things found that, when thought deeply about, the concept of a characteristic function is, in fact, itself rather deep.

You arrive at topos theory simply by taking the concept of a characteristic function and forgetting that it is a statement about sets.

More generally, it could happen that, in some context to be specified, there are things $K$ which may have sub-things $S \subset K$ sitting inside them, and such that to every sub-thing of $K$ there uniquely corresponds an arrow from the big thing $K$ to some special thing $\Omega$ $(S \subset K) \leftrightarrow (\chi_S : K \to \Omega) \,.$

In the motivating example, the “things” were sets, the “arrows” were functions between sets and the “special thing” $\Omega$ was the two-element set $\{0,1\}$ .

But there might be other contexts in which the relation $(S \subset K) \leftrightarrow (\chi_S : K \to \Omega)$ makes sense. If it does, the context is called a topos.

That’s it.

These simple ideas become powerful once one realizes that the business called logic is essentially the study of characteristic functions.

When we come from that point of view, we’d regard the set $K$ as a set of “states” (for instance the set of configurations of a physical system) and we regard a function $F : K \to \{0,1\}$ as a proposition about these states $F : k \mapsto \left\lbrace \array{ 1 & if the proposition is true for k \\ 0 & otherwise } \right. \,.$

For instance, to stay in the class of examples that we were talking about in The Principle of General Tovariance, the proposition $F$ might be:

$F$ : the system has an energy in between 5 and 10 Joule

But this also means means:

$F$ is simply the characteristic function of the subset of configurations of the system whose energy is in between 5 and 10 Joule.

So in summarry we find that, in the context of sets, $\array{ subsets \\ = \\ characteristic functions \\ = \\ propositions } \,.$

This means that if we pick any other context in which

subsets = characteristic functions,

namely a topos, we may just as well interpret everything we do in that topos as being about propositions.

And that’s what people do.

As a slogan:

A topos is a context in which sub-things correspond to chracteristic arrows, and hence the concept of a proposition makes sense.

Posted by: Urs Schreiber on December 12, 2007 10:43 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

From the peanut gallery: Thank you, Urs, for this wonderful, simple topos explanation with easy-to-understand examples. They are few and far between. I should tear it out and paste it to the inside cover of my copy of Conceptual Mathematics; A first introduction to categories by Lawvere and Schanuel. As I lumber down the runway trying to achieve take-off speed and climb even a few feet above the ground, I can use all the help I can get. And thank you, Eric, for asking the question. You guys all set an impossible goal for me to strive for, but the trip is worth the effort.

Posted by: Charlie C on December 12, 2007 8:46 PM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

Hi Charlie,

Keep up the good work and don’t be discouraged. I remember when Urs was first learning differential forms and “I” could help “him” with stuff. Ah, the good ol’ days :) From there, he quickly leapfrogged me and if you hang around with these guys long enough, I have no doubt you’ll leapfrog me too (not that that is such a hurdle). I’ve long ago thrown in the towel and this cafe is my only connection left to anything scientific (until I can get Urs interested in modeling yield curve dynamics as a Black-Scholes equation on “yield curve space”) :)

And Urs,

I second Charlies words of thanks. Those explanations were so clear, I can almost fool myself into believing I understood them :)

If what you described is what “topos” is really trying to explain, then “topoi” have been close to my heart from the beginning without me knowing it. It would be fun to go back over our discrete geometry stuff and interpret it in terms of characteristic functions.

Given some countable set of “nodes” $e_i$ , then we have a countable set of “characteristic functions” $e^j$ with

(1)

e^j(e_i) = \delta^j_i.

The sum of characteristic functions is the unit element

(2)

1 = \sum_j e^j

The product of characteristic functions is defined in the obvious way

(3)

(e^j e^k)(e_i) = e^j(e_i) e^k(e_i)

which can be written as

(4)

e^j e^k = \delta^{jk} e^j.

Look familiar? :)

Then you can introduce the differential of characteristic functions satisfying

(5)

d(e^j e^k) = (de^j) e^k + e^j (de^k) = \delta^{jk} de^j

and

(6)

d^2 = 0

where

(7)

[de^j,e^k] \ne 0

since otherwise $e^i de^j = 0$ for all $i$ and $j$ .

An (dual?) edge (or morphism?) from $e_i$ to $e_j$ can then be represented as

(8)

e^{ij} = e^i (de^i) e^j = -e^i (de^j) e^j.

Then you’re off and running. We could have called our paper “differential topos” or something :)

And to throw in one additional whacky thought for good measure, you could argue (if you were whacky and lacking brain cells) that differential topoi must be noncommutative.

Posted by: Eric on December 13, 2007 5:59 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

If what I wrote makes ANY sense (which would be miraculous), then since topos describe “logic” then a differential topoi would describe “differential logic”. For example, what is something that connects “propositions”? “States” are like nodes of a graph and “Propositions” are dual to states (and hence like “dual nodes” of a graph). “Morphisms” (edges) as mappings from one state (node) to another (node) makes sense, but what is dual to a “morphism”? The “differential” of a “proposition” is dual to morphisms between states.

I know I’m totally off and have the whole concept totally confused, but does anything in there make the least bit of sense? If so, I think I might be starting to understand “arrow theory” a little bit. It’s kind of like graph calculus framed in the language of logic (or vice versa). Life cannot be that good, so I’m almost surely spewing random nonsense.

Posted by: Eric on December 13, 2007 6:18 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

$MathML-enabled post (click for more details).$

Eric wrote:

we have a countable set of “characteristic functions”

[…]

“differential topos” or something

But notice: here you are using the topos of sets and remain well within its boundaries. Using a bunch of characteristic functions in Set to do something is different from constructing a new topos.

Posted by: Urs Schreiber on December 13, 2007 11:43 AM | Permalink | Reply to this

Re: Local Nets from 2-Transport

See? That is why I should stick to lurking :)

Posted by: Eric on December 14, 2007 4:06 AM | Permalink | Reply to this

Read the post The Concept of a Space of States, and the Space of States of the Charged n-Particle
Weblog: The n-Category Café
Excerpt: On the notion of topos-theoretic quantum state objects, the proposed definition by Isham and Doering and a proposal for a simplified modification for the class of theories given by charged n-particle sigma-models.
Tracked: January 10, 2008 10:32 AM

Read the post What has happened so far
Weblog: The n-Category Café
Excerpt: A review of one of the main topics discussed at the Cafe: Sigma-models as the pull-push quantization of nonabelian differential cocycles.
Tracked: March 27, 2008 2:20 PM

Read the post Relation between AQFT and Extended Functorial QFT
Weblog: The n-Category Café
Excerpt: On how to obtain from any extended d-dimensional QFT a local net of observables.
Tracked: May 20, 2008 9:56 AM

The n-Category Café

Skip to the Main Content

December 9, 2007