Theorems Into Coffee IV
Posted by John Baez
I’m in Paris now. I’ve spent this week attending a conference on Algebraic Topological Methods in Computer Science. Yesterday during one of the breaks my host, Paul–André Melliès, introduced me to a student I’d seen somewhere before. I didn’t catch the guy’s name, but his eyes glittered strangely as we sipped our coffee and talked, and then I realized: it was Samuel Mimram, winner of the first Theorems Into Coffee challenge! In this paper:
- Samuel Mimram, Presentation of a game semantics for first-order propositional logic, Thm. 14, page 22.
he proved the result I sought, namely:
Theorem: is the PROP for bicommutative bimonoids.
So, I handed him an elegant handmade Korean envelope containing 20 euros — to be spent only on coffee.
I’m not sure how my offered prize of 15 dollars turned into 20 euros. I must have been in a good mood.
Earlier at the same conference I spoke to Eugenia Cheng about her work on the Theorems into Coffee problems, and we wound up studying this paper by Steve Lack:
-
Steve Lack, Composing
PROPs, Theory and Applications of Categories 13 (2004), 147–163.
Abstract: A PROP is a way of encoding structure borne by an object of a symmetric monoidal category. We describe a notion of distributive law for PROPs, based on Beck’s distributive laws for monads. A distributive law between PROPs allows them to be composed, and an an algebra for the composite PROP consists of a single object with an algebra structure for each of the original PROPs, subject to compatibility conditions encoded by the distributive law. An example is the PROP for bialgebras, which is a composite of the PROP for coalgebras and that for algebras.
It’s very nice, and Lack probably deserves several kilos of coffee. Let me quickly sketch some of his results before proposing the next Theorems Into Coffee problem.
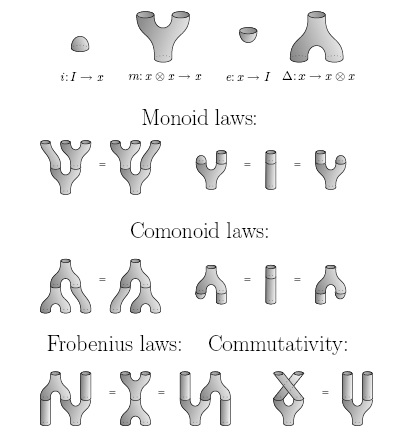
I’ve already explained PROPs and their algebras, but let me remind you of the official definition:
Definition: A PROP is a strict symmetric monoidal category with natural numbers as objects, for which the tensor product of objects and is . Given a symmetric monoidal category , an algebra of in is a symmetric monoidal functor , and a morphism of algebras is a symmetric monoidal natural transformation between such functors. There is a category of algebras of in .
However, it’s sometimes convenient to relax our definition a bit and consider any symmetric monoidal category that’s equivalent to a PROP to again be a PROP. This amounts to saying:
Definition: A relaxed PROP is a symmetric monoidal category with an object such that every object is isomorphic to one of the form .
If we then define algebras and morphisms between algebras as before, it’s clear that for every relaxed PROP there is a PROP with an equivalent category of algbras. So, we’re not losing anything, or gaining anything… except that sometimes it’s easier or more fun to describe the relaxed version of a PROP.
For example, I’ve already mentioned a PROP called , where the morphisms from to are matrices of natural numbers, and composing morphisms is done by matrix multiplication. This is nice, but there’s a more conceptual way to think about it as a relaxed PROP: namely, the category where the objects are finite sets, the morphisms are spans of finite sets, and we compose spans by pullback. I call this category .
(Actually, to be perfectly honest, I’ve just described a bicategory rather than a category, since composition of spans is associative only up to isomorphism! But we can take isomorphism classes of spans and get a category — and that’s what I’ll do. So, just for today, I’m secretly using ‘span’ to mean ‘isomorphism class of span’.)
In Section 5.3 of his paper, Steve Lack proves a result equivalent to Samuel Mimram’s result mentioned above:
Theorem: is the relaxed PROP for bicommutative bimonoids.
By this I mean that the category of algebras of in any symmetric monoidal category is equivalent to the category of bicommutative bimonoids in .
The interesting thing is that Lack has a very conceptual way to prove this sort of result, not involving string diagrams (as in Mimram’s proof) or matrices (as in Simon Wadsley’s). Instead, he uses a way of tensoring two PROPs given a rule that says how to slide operations of one past operations of the other. This rule should probably be called a ‘commutative law’ or ‘braiding’, but the term ‘distributive law’ is traditional, since the old-fashioned distributive law
is an example: it tells you how to switch from adding first and then multiplying to multiplying first and then adding!
In particular, Lack starts by proving this:
Theorem: is the relaxed PROP for commutative monoids.
where is the category of finite sets and functions. It’s then easy to see:
Theorem: is the relaxed PROP for cocommutative comonoids.
Then, using a certain distributive law to tensor these two PROPs, he shows
Theorem: is the relaxed PROP for bicommutative bimonoids.
Even if you don’t quite follow what’s going on, this should have a ring of plausibility. Every operation for a bicommutative bimonoid can be achieved by first doing a bunch of comultiplications and then a bunch of multiplications. Similarly, every span in looks like this:
so we’re first doing a morphism in and then a morphism in . A morphism in is just what we need to describe a bunch of comultiplications; a morphism in is just what we need to describe a bunch of multiplications!
Charmingly, Lack also shows:
Theorem: is the relaxed PROP for commutative separable algebras.
If I remember correctly, a separable algebra is one where the bilinear form is nondegenerate, where means left multiplication by . This makes into a Frobenius algebra with the special property that comultiplication followed by multiplication is the identity!
So, a commutative separable algebra is a specially nice Frobenius algebra — maybe just a commutative Frobenius algebra where comultiplication followed by multiplication is the identity.
Note: I’ve slipped into terminology that people use in the category of vector spaces, like calling a monoid an ‘algebra’. But, everything I’m saying makes sense in any symmetric monoidal category. So, you might prefer to cross out ‘algebra’ wherever you see it, and write in ‘monoid’. Go ahead — just don’t damage your computer screen!
But the point is this:
It’s really easy for beginners to get mixed up between bialgebras and Frobenius algebras, since they both have a multiplication and comultiplication, and some classic examples, like the group algebra of a finite group, are both bialgebras and Frobenius algebras. Now we’re seeing a deep relationship between the two, which shows that the beginner’s confusion is not purely stupid.
(There’s at least one other deep relationship, too. A bialgebra may be defined as an algebra that’s also a coalgebra, such that all the coalgebra operations are algebra homomorphisms. A Frobenius algebra may be defined as an algebra that’s also a coalgebra, such that all the coalgebra operations are -bimodule homomorphisms!)
Lack also describes the PROP for bialgebras… or, if you prefer, bimonoids. This was going to be my next coffee problem, since James Dolan and I had worked out this PROP after quite a bit of struggle and confusion, and I wanted someone to give a nice proof. Here’s the answer:
First, let be the relaxed PROP where the objects are finite sets and the morphisms are functions where each fiber is equipped with a linear ordering. Lack shows:
Theorem: is the relaxed PROP for monoids.
The point is that we don’t know how to multiply a bunch of guys in a monoid unless we know what order they’re in. Similarly:
Theorem: is the relaxed PROP for comonoids.
and using a certain distributive law to tensor the two:
Theorem: is the relaxed PROP for bimonoids.
This PROP is a bit strange. A morphism in this PROP is just a span in , but we don’t compose these spans by pullback! Instead, we need to insert a ‘fiendish twist’. You can see this as a permutation called in the very last diagram of Lack’s paper — a permutation that turns the usual pullback square into a pentagon.
This fiendish twist arises from the fact that there are two natural ways to make the cartesian product of totally ordered sets into a totally ordered set: the lexicographic ordering and the reverse lexicographic ordering.
And, it’s this ‘fiendish twist’ that’s the really interesting thing about the PROP for bimonoids. It gave James and Eugenia and me many hours of suffering and delight!
Alas, I’m getting too worn out to explain it properly here, so let me just say this: Ponder the PROP for bimonoids, try to describe it as above, think about how to compose the operations, and you will discover the fiendish twist.
Now let me pose the fourth Theorems Into Coffee problem — for a prize of 15 dollars worth of coffee, under the usual terms and conditions:
Coffee Problem: Give an elegant description of the PROP for Hopf algebras.
This is more open-ended than the previous ones…

Re: Theorems Into Coffee IV
Here’s another question: what about ?
(I should admit that what I’m calling , Lack calls , written in blackboard bold.)