Division Algebras and Supersymmetry
Posted by John Baez
I’ve been in love with the octonions for over a decade now. They seem downright distasteful when you first meet them: an 8-dimensional algebra where division is allowed, but multiplication is nonassociative! Only later do you realize that they’re deeply connected to a wide range of mysterious and exotic things: the icosahedron, the exceptional Lie groups, the exceptional Jordan algebra… and the way superstring theory and super-Yang–Mills theory love to live in 10 dimensions.
I wrote a paper on the octonions back in 2001, where I tried to assemble all the clues I’d found. But I didn’t get far in relating the octonions to supersymmetry. I just explained the basic facts: how octonions are naturally tied to 10-dimensional Minkowski spacetime.
Now I’m lucky to have a brave graduate student who can do calculations like a physicist and proofs like a mathematician: John Huerta. Since March — when we finished our review article on the algebra of grand unified theories — we’ve been digging into the relation between octonions and supersymmetry. As so often the case in this game, the clues are already available, lurking in existing papers. The trick is assembling them into a clear story that people can understand without going on a lengthy and painful quest.
- John Baez and John Huerta, Division algebras and supersymmetry — latest version with all known corrections or arXiv version.
It’s not quite done yet, but it’s close. As always, comments and corrections would be appreciated.
In a way, the story is very simple. In Minkowski spacetime of any dimension, there’s an operation
that takes two spinors and turns them into a vector. There’s also an operation
whereby a vector acts on a spinor and gives another spinor. In fact these two operations are just two views of the same thing: the basic interaction between spinors and vectors. We see this interaction — very literally, we see it — whenever light hits an electron in our eyes. The photon is a vector, the electron is a spinor, and the absorption process involves the operation . In Feynman diagram language, it looks like this:
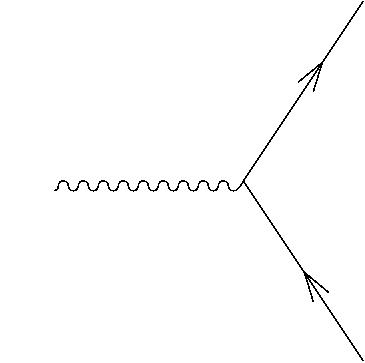
Now, given a spinor , we can define a new spinor by combining the above two maps:
And then comes something magic:
Theorem: for all if and only if the dimension of spacetime is 3, 4, 6, or 10.
Our paper gives a proof of the ‘if’ part. The idea is this: these four magic dimensions are 2 more than the dimensions of the normed division algebras and . We can use the division algebras to describe spinors and vectors in these magic dimensions. A special feature of the normed division algebras make the identity true. Namely, in these algebras the associator
is completely antisymmetric.
The proof is just algebra, and you don’t need to know any physics to follow it. So every mathematician in the universe should read this portion of the paper (Section 2).
We also explain how the identity gives rise to supersymmetry in Yang–Mills theory in dimensions 3, 4, 6, and 10. This part takes a bit more physics know-how — or at least, differential geometry.
By the way, this identity also shows up when checking supersymmetry for the Green-Schwarz Lagrangian of the classical superstring! So, it really rules the world… at least if you believe in supersymmetry.
Also by the way, I’ve been very sloppy above about left-handed versus right-handed spinors, and also Weyl, Majorana and Majorana–Weyl spinors. The paper is not sloppy in this way.
Lastly, on a more personal note: this is the last paper I need to write for a while! I did a calculation and discovered that after this one is done, I’ll have put 471 pages of papers on the arXiv since December 29th of last year. Spending all my time finishing half-written papers, some of which have been hanging over my head for years, has made me stressed-out, irritable and gloomy. But putting them off, which I’d been doing earlier, made me feel even worse. So it’s a great relief to be done, and I plan to live a happy-go-lucky, carefree, irresponsible life from now on.

Re: Division Algebras and Supersymmetry
I think that there are sign errors in the proof of Proposition 2 on Page 3. It should read:
“Since (ab)∗ = b∗a∗ , we have [a, b, c]∗ = -[c∗ , b∗ , a∗ ]. By alternativity this equals
[a∗, b∗ , c∗ ],
which in turn equals
−[a, b, c] by the above proposition. So, [a, b, c] is purely imaginary.”
Yours has the opposite signs written for [c∗ , b∗ , a∗ ] and [a∗, b∗ , c∗ ].