Apart from the whisky-session, anything noteworthy?
(This question is meant to be addressing anyone who attended. I am aware that John might be offline travelling across the continents.)
I am looking at the abstracts.
I have some idea of what John was talking about in “Duality in Logic and Physics”.
John Barrett’s abstract is
John Barrett: State sum models, induced gravity and the spectral action
I will give a new proposal for the spectral action for gravity coupled to matter, taking into account the phenomenon of induced gravity. This is then used to give some perspectives for the construction of a quantum theory of gravity coupled to matter using state sum models based on a tricategory.
Is “spectral action” here meant in the sense of Connes, Chamseddine et al? A functional on a space of spectral triples that evaluates to something close to the Einstein-Hilbert action coupled to this and that in the case that the Dirac operator of the triple is one for an ordinary Riemannian manifold?
What tricategory does he consider?
Louis Crane’s abstract begins with
Louis Crane, The category of spacetime regions
The purpose of this talk is to propose a connection between the spin foam approach to quantum gravity and a branch of abstract homotopy theory called model category theory.
Ah! See -categories enter the field of state sum models for quantum gravity.
It continues:
The spin foam approach models regions in spacetime by four dimensional simplicial complexes. The quantum theory of the metric on them is constructed by putting representations of the Lorentz group on the triangulation and combining them in a specific way, called a categorical state sum. Recently a technical advance has removed the problems that plagued the theory, so that a finite computational theory of quantum general relativity seems to be available. The deeper interpretational problems remain: what do the specific complexes mean? Are they triangulations of an underlying point set, or Feynman diagrams of a fundamental theory? If they are just approximations, how does the exact theory emerge? How does the Bekenstein bound relate to this picture? How does the classical limit of the models approach general relativity?
Any specific answers to these questions?
And then:
What we are going to propose is that the state sum models on different simplicial complexes can be modified to fit together to form what is called a model category.
What are the weak equivalences?
We can then incorporate the Bekenstein bound into the model by using a technique from model category theory called localization. The flow of information from a system to its exterior would be a map in the category,
Hm, above it sounded as if the objects of the model category are supposed to be state sum models on different simplicial complexes. How would a morphism of such encode “the flow of information from a system to its exterior”??
and the localization of a model of the system with respect to this map would give a simplicial complex on which the exact effective theory would be computed.
Hm, does this refer to taking a state sum model on some simplicial complex and then passing to a fibrant-cofibrant replacement?
Does anyone have more details?







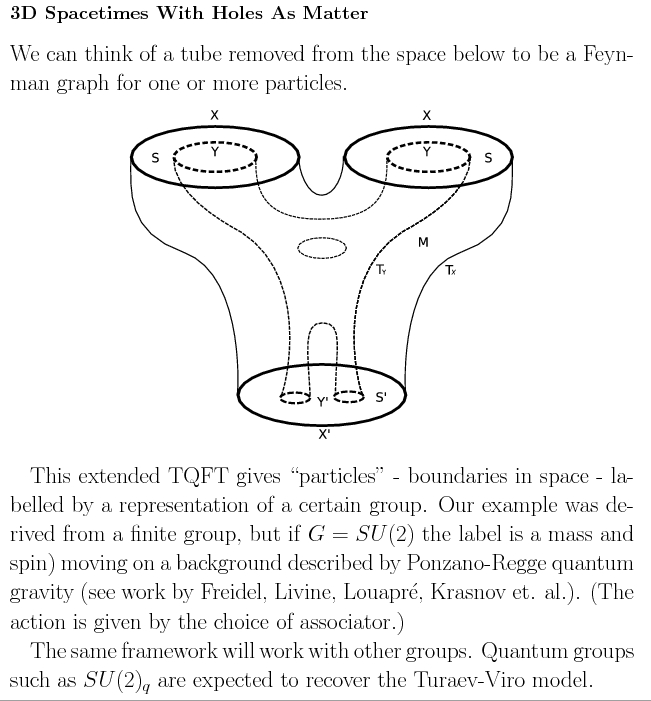

Re: The Quantum Whisky Club
Hi folks, here’s a pic of John liveblogging for the above post…!