Heron’s Formula
Posted by John Baez
guest post by J. Scott Carter
An undergraduate student, David Mullens, and I recently posted a paper that presents a 4-dimensional proof of Heron’s formula. (Caution: it’s about 2.5 megabytes in size.)
You may recall from your high school geometry class that Heron’s formula tells how to compute the area of a triangle given its side lengths. The form that I want to present the formula is as follows:
where indicates the area of the triangle, and the side lengths are , and . By convention we choose variables so that is no greater than which is no greater than . Traditionally, Heron’s formula is stated in terms of the semi-perimeter, but our purpose is to demonstrate that two hyper-volumes (4-dimensional analogues of volume) are actually scissors congruent.
Our motivations came from various conversations in various places. So I will relate the personal details before the technical details.
Abhijit Champanerkar and I indicated in this paper a higher dimensional interpretation of the fact that the integral of an th power (over the unit interval) is the -dimensional volume of a pyramidal structure whose base is the -cube. We did not know of the paper of Nils Barth, Computing Cavalieri’s Quadrature Formula By a Symmetry of the n-Cube, American Mathematical Monthly, 111 (2004), no. 9, 811-813, who had discovered essentially the same thing, so we have let our manuscript sit on the arXiv.
The proof that Barth gives and that we give is a nice dinner-time or tea-time story that can be related to the mathematician who is higher-dimensionally inclined. During one such conversation in Hanoi, Dylan Thurston asked us if we knew of a -dimensional proof that the sum of the cubes of consecutive integers is the square of the corresponding triangular number. From the point of view of using Bernoulli numbers to sum th powers, the context of Dylan’s question is quite natural. Dylan reported the proof which he, Dave Bayer, and Walter Neumann had discovered at a dinner conversation. The proof involved splitting the cube into two prisms, taking the cone on each and reassembling them into the hyper-solid that is a triangle times a triangle.
The conversation with Dylan stimulated me to use a -dimensional projection of a right isosceles triangle times the same as a model for some artistic sketches that were made in homage to the artist Tony Robbin. These appear here . At a conference on art and math in Tampa, Florida, I showed some of these works as part my slides and mentioned the mathematics of the preceding two paragraphs to John H. Conway over dinner. At that point, Conway mentioned that he sought a 4-dimensional proof of Heron’s formula.
Mullens, who is a mathematics and statistics major at the University of South Alabama, had taken to posting short problems on a hallway blackboard in a “Good Will Hunting” sort of a way. The problems were various jewels from a variety of math problem solving books that we keep available in the department. A few of these had to do with applications of Heron’s formula, and so I gave Mullens the Heron’s formula problem to work upon.
The proof in our paper relies upon a scissors congruence proof of the Pythagorean Theorem. Any such proof is sufficient, but we explicitly use the one in which a square with edge length is decomposed into four right triangles (with legs of length and ) and a central square of edge length , as indicated here for example.
It is fairly easy to see that the distributive law is a scissors congruence, and we spent some time in the paper to discuss the scissors congruence properties when negative edge lengths are involved.
Our major lemma is that if polygons and are respectively scissors congruent to and , then the hyper-solids and are scissors congruent. This result follows, roughly, from the fact that cartesian products distribute over unions. More explicitly, we examine dihedral angles between facets of the hyper-solids. Within the figures, we develop in detail the scissors congruence for the product of two proofs of the Pythagorean theorem.
Finally, we examine the high school algebra proofs in terms of the scissors congruences outlined above. The expression , where is the area of the triangle, represents the volume of four hyper-parallelograms (parallelogram times parallelogram), each of which is decomposed into four copies of a triangle times triangle. The expression is the hyper-volume of a hyper-rectangle. It is decomposed into pieces via the distributive law. All but nine terms in this expression cancel. Some of those nine terms will further decomposed using the proof of the Pythagorean theorem.

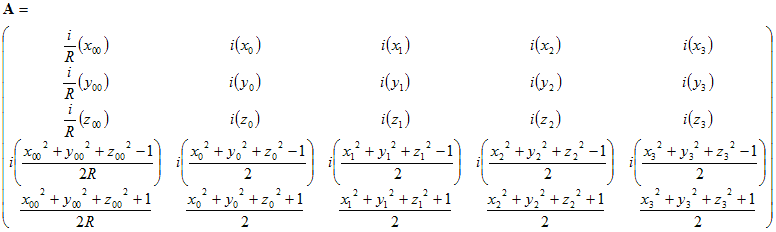
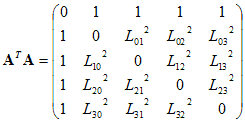
Re: Heron’s Formula
Readers who enjoy higher-dimensional proofs by dissection should go back and look at our blog entry on Categorifying Nichomachus of Gerasa’s Equation.
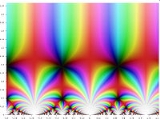
Here’s a pretty picture from Scott Carter’s new paper showing how the usual dissection of a square into triangles gives a dissection of a hypercube into four shapes, each the product of two triangles.
It’s about the simplest picture in the paper!