The Tenfold Way (Part 1)
Posted by John Baez
There are 10 of each of these things:
Associative real super-division algebras.
Classical families of compact symmetric spaces.
Ways that Hamiltonians can get along with time reversal () and charge conjugation () symmetry.
Dimensions of spacetime in string theory.
It’s too bad nobody took up writing This Week’s Finds in Mathematical Physics when I quit. Someone should have explained this stuff in a nice simple way, so I could read their summary instead of fighting my way through the original papers. I don’t have much time for this sort of stuff anymore!
Luckily there are some good places to read about this stuff:
Todd Trimble, The super Brauer group and super division algebras, April 27, 2005.
Shinsei Ryu, Andreas P. Schnyde, Akira Furusaki and Andreas W. W. Ludwig, Topological insulators and superconductors: tenfold way and dimensional hierarchy, June 15, 2010.
Gregory Moore and Dan Freed, Twisted equivariant matter, January 7, 2013.
Gregory Moore, Quantum symmetries and compatible Hamiltonians, December 15, 2013.
Let me start by explaining the basic idea, and then move on to more fancy aspects.
Ten kinds of matter
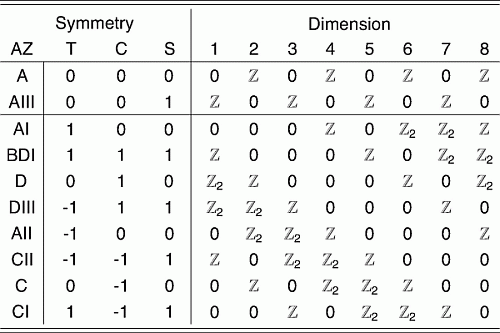
The idea of the ten-fold way goes back at least to 1996, when Altland and Zirnbauer discovered that substances can be divided into 10 kinds.
The basic idea is pretty simple. Some substances have time-reversal symmetry: they would look the same, even on the atomic level, if you made a movie of them and ran it backwards. Some don’t — these are more rare, like certain superconductors made of yttrium barium copper oxide! Time reversal symmetry is described by an antiunitary operator that squares to 1 or to -1: please take my word for this, it’s a quantum thing. So, we get 3 choices, which are listed in the chart under as 1, -1, or 0 (no time reversal symmetry).
Similarly, some substances have charge conjugation symmetry, meaning a symmetry where we switch particles and holes: places where a particle is missing. The ‘particles’ here can be rather abstract things, like phonons - little vibrations of sound in a substance, which act like particles — or spinons — little vibrations in the lined-up spins of electrons. Basically any way that something can wave can, thanks to quantum mechanics, act like a particle. And sometimes we can switch particles and holes, and a substance will act the same way!
Like time reversal symmetry, charge conjugation symmetry is described by an antiunitary operator that can square to 1 or to -1. So again we get 3 choices, listed in the chart under as 1, -1, or 0 (no charge conjugation symmetry).
So far we have 3 × 3 = 9 kinds of matter. What is the tenth kind?
Some kinds of matter don’t have time reversal or charge conjugation symmetry, but they’re symmetrical under the combination of time reversal and charge conjugation! You switch particles and holes and run the movie backwards, and things look the same!
In the chart they write 1 under the when your matter has this combined symmetry, and 0 when it doesn’t. So, “0 0 1” is the tenth kind of matter (the second row in the chart).
This is just the beginning of an amazing story. Since then people have found substances called topological insulators that act like insulators in their interior but conduct electricity on their surface. We can make 3-dimensional topological insulators, but also 2-dimensional ones (that is, thin films) and even 1-dimensional ones (wires). And we can theorize about higher-dimensional ones, though this is mainly a mathematical game.
So we can ask which of the 10 kinds of substance can arise as topological insulators in various dimensions. And the answer is: in any particular dimension, only 5 kinds can show up. But it’s a different 5 in different dimensions! This chart shows how it works for dimensions 1 through 8. The kinds that can’t show up are labelled 0.
If you look at the chart, you’ll see it has some nice patterns. And it repeats after dimension 8. In other words, dimension 9 works just like dimension 1, and so on.
If you read some of the papers I listed, you’ll see that the ’s and ’s in the chart are the homotopy groups of the ten classical series of compact symmetric spaces. The fact that dimension works like dimension is called Bott periodicity.
Furthermore, the stuff about operators , and that square to 1, -1 or don’t exist at all is closely connected to the classification of associative real super division algebras. It all fits together.
Super division algebras
In 2005, Todd Trimble wrote a short paper called The super Brauer group and super division algebras.
In it, he gave a quick way to classify the associative real super division algebras: that is, finite-dimensional associative real -graded algebras having the property that every nonzero homogeneous element is invertible. The result was known, but I really enjoyed Todd’s effortless proof.
However, I didn’t notice that there are exactly 10 of these guys. Now this turns out to be a big deal. For each of these 10 algebras, the representations of that algebra describe ‘types of matter’ of a particular kind — where the 10 kinds are the ones I explained above!
So what are these 10 associative super division algebras?
3 of them are purely even, with no odd part: the usual associative division algebras and .
7 of them are not purely even. Of these, 6 are Morita equivalent to the real Clifford algebras and . These are the superalgebras generated by 1, 2, 3, 5, 6, or 7 odd square roots of -1.
Now you should have at least two questions:
What’s ‘Morita equivalence’? — and even if you know, why should it matter here? Two algebras are Morita equivalent if they have equivalent categories of representations. The same definition works for superalgebras, though now we look at their representations on super vector spaces (-graded vector spaces). For physics what we really care about is the representations of an algebra or superalgebra: as I mentioned, those are ‘types of matter’. So, it makes sense to count two superalgebras as ‘the same’ if they’re Morita equivalent.
1, 2, 3, 5, 6, and 7? That’s weird — why not 4? Well, Todd showed that is Morita equivalent to the purely even super division algebra . So we already had that one on our list. Similarly, why not 0? is just . So we had that one too.
Representations of Clifford algebras are used to describe spin-1/2 particles, so it’s exciting that 8 of the 10 associative real super division algebras are Morita equivalent to real Clifford algebras.
But I’ve already mentioned one that’s not: the complex numbers, , regarded as a purely even algebra. And there’s one more! It’s the complex Clifford algebra . This is the superalgebra you get by taking the purely even algebra and throwing in one odd square root of -1.
As soon as you hear that, you notice that the purely even algebra is the complex Clifford algebra . In other words, it’s the superalgebra you get by taking the purely even algebra and throwing in no odd square roots of -1.
More connections
At this point things start fitting together:
You can multiply Morita equivalence classes of algebras using the tensor product of algebras: . Some equivalence classes have multiplicative inverses, and these form the Brauer group. We can do the same thing for superalgebras, and get the super Brauer group. The super division algebras Morita equivalent to serve as representatives of the super Brauer group of the real numbers, which is . I explained this in week211 and further in week212. It’s a nice purely algebraic way to think about real Bott periodicity!
As we’ve seen, the super division algebras Morita equivalent to and are a bit funny. They’re purely even. So they serve as representatives of the plain old Brauer group of the real numbers, which is .
On the other hand, the complex Clifford algebras and serve as representatives of the super Brauer group of the complex numbers, which is also . This is a purely algebraic way to think about complex Bott periodicity, which has period 2 instead of period 8.
Meanwhile, the purely even and underlie Dyson’s ‘three-fold way’, which I explained in detail here:
- John Baez, Division algebras and quantum theory.
Briefly, if you have an irreducible unitary representation of a group on a complex Hilbert space , there are three possibilities:
The representation is isomorphic to its dual via an invariant symmetric bilinear pairing . In this case it has an invariant antiunitary operator with . This lets us write our representation as the complexification of a real one.
The representation is isomorphic to its dual via an invariant antisymmetric bilinear pairing . In this case it has an invariant antiunitary operator with . This lets us promote our representation to a quaternionic one.
The representation is not isomorphic to its dual. In this case we say it’s truly complex.
In physics applications, we can take to be either time reversal symmetry, , or charge conjugation symmetry, . Studying either symmetry separately leads us to Dyson’s three-fold way. Studying them both together leads to the ten-fold way!
So the ten-fold way seems to combine in one nice package:
- real Bott periodicity,
- complex Bott periodicity,
- the real Brauer group,
- the real super Brauer group,
- the complex super Brauer group, and
- the three-fold way.
I could throw ‘the complex Brauer group’ into this list, because that’s lurking here too, but it’s the trivial group, with as its representative.
There really should be a better way to understand this. Here’s my best attempt right now.
The set of Morita equivalence classes of finite-dimensional real superalgebras gets a commutative monoid structure thanks to direct sum. This commutative monoid then gets a commutative rig structure thanks to tensor product. This commutative rig — let’s call it — is apparently too complicated to understand in detail, though I’d love to be corrected about that. But we can peek at pieces:
We can look at the group of invertible elements in — more precisely, elements with multiplicative inverses. This is the real super Brauer group .
We can look at the sub-rig of coming from semisimple purely even algebras. As a commutative monoid under addition, this is , since it’s generated by and . This commutative monoid becomes a rig with a funny multiplication table, e.g. . This captures some aspects of the three-fold way.
We should really look at a larger chunk of the rig , that includes both of these chunks. How about the sub-rig coming from all semisimple superalgebras? What’s that?
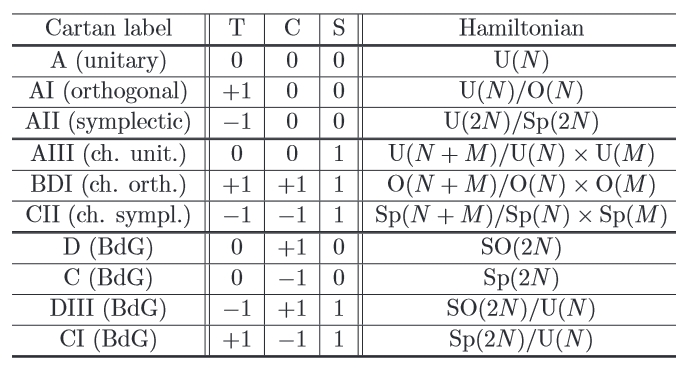
And here’s another question: what’s the relation to the 10 classical families of compact symmetric spaces? The short answer is that each family describes a family of possible Hamiltonians for one of our 10 kinds of matter. For a more detailed answer, I suggest reading Gregory Moore’s Quantum symmetries and compatible Hamiltonians. But if you look at this chart by Ryu et al, you’ll see these families involve a nice interplay between and , which is what this story is all about:
The families of symmetric spaces are listed in the column “Hamiltonian”.
All this stuff is fitting together more and more nicely! And if you look at the paper by Freed and Moore, you’ll see there’s a lot more involved when you take the symmetries of crystals into account. People are beginning to understand the algebraic and topological aspects of condensed matter much more deeply these days.
The list
Just for the record, here are all 10 associative real super division algebras. 8 are Morita equivalent to real Clifford algebras:
is the purely even division algebra .
is the super division algebra , where is an odd element with .
is the super division algebra , where is an odd element with and .
is the super division algebra , where is an odd element with and .
is , the algebra of quaternionic matrices, given a certain -grading. This is Morita equivalent to the purely even division algebra .
is given a certain -grading. This is Morita equivalent to the super division algebra where is an odd element with and .
is given a certain -grading. This is Morita equivalent to the super division algebra where is an odd element with and .
is given a certain -grading. This is Morita equivalent to the super division algebra where is an odd element with .
is Morita equivalent to so we can stop here if we’re just looking for Morita equivalence classes, and there also happen to be no more super division algebras down this road. It is nice to compare and : there’s a nice pattern here.
The remaining 2 real super division algebras are complex Clifford algebras:
is the purely even division algebra .
is the super division algebra , where is an odd element with and .
In the last one we could also say “with ” — we’d get something isomorphic, not a new possibility.
Ten dimensions of string theory
Oh yeah — what about the 10 dimensions in string theory? Are they really related to the ten-fold way?
It seems weird, but I think the answer is “yes, at least slightly”.
Remember, 2 of the dimensions in 10d string theory are those of the string worldsheet, which is a complex manifold. The other 8 are connected to the octonions, which in turn are connected to the 8-fold periodicity of real Clifford algebra. So the 8+2 split in string theory is at least slightly connected to the 8+2 split in the list of associative real super division algebras.
This may be more of a joke than a deep observation. After all, the 8 dimensions of the octonions are not individual things with distinct identities, as the 8 super division algebras coming from real Clifford algebras are. So there’s no one-to-one correspondence going on here, just an equation between numbers.
Still, there are certain observations that would be silly to resist mentioning.

Re: The Ten-Fold Way
Of course, the real fun starts with the exceptional cases, i.e. G/H for G an exceptional group. The condensed matter guys haven’t really considered these cases but there already exists an interpretation within supergravity via toroidal M-theory compactifications.