The n-Category Café

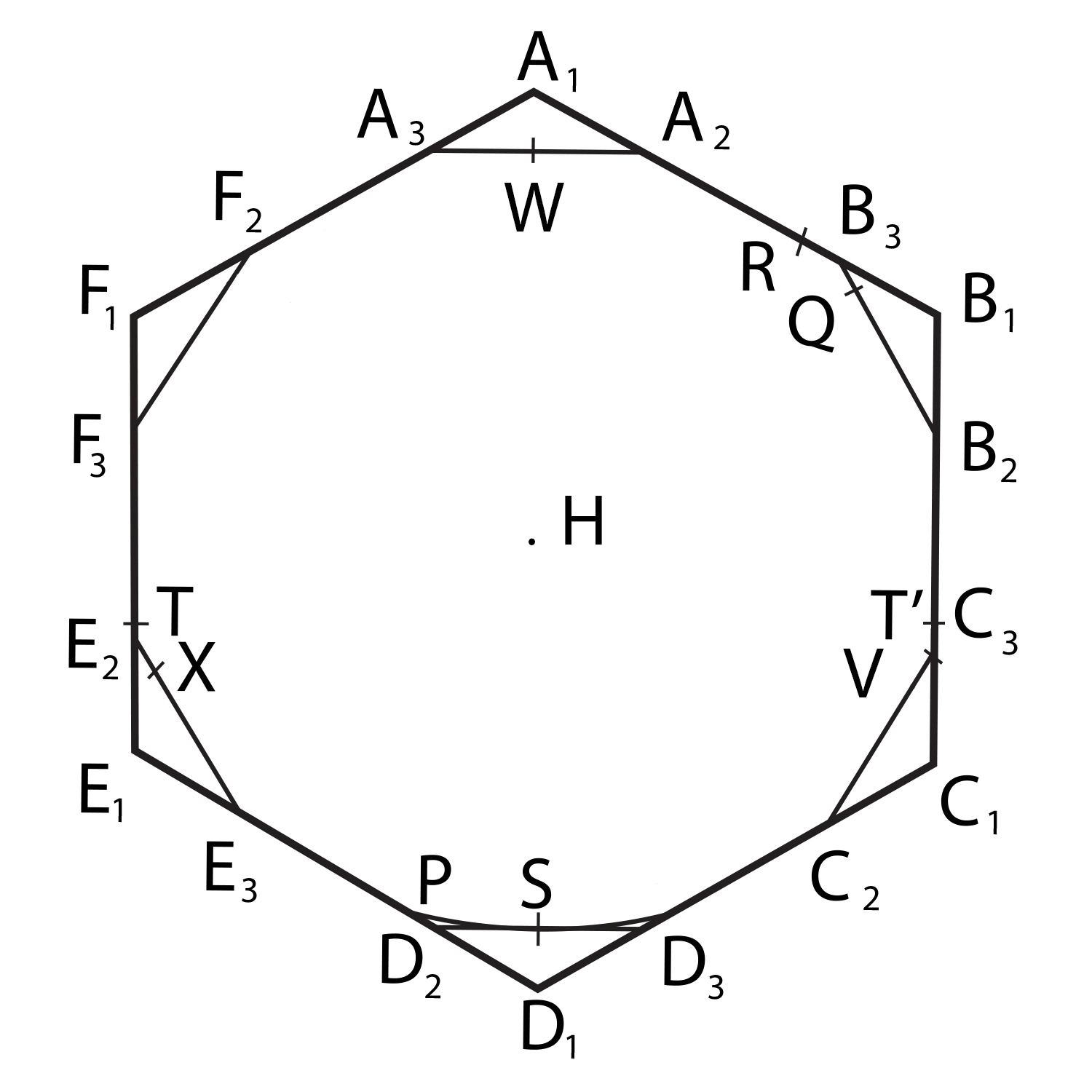
I’m not sure that this is entirely on-topic, but I’ve been pondering ways to approach the construction of a universal covering systematically, and I came up with a method that I think is quite interesting … although alas it gives a pretty useless area of about 0.85.

Any set $S$ of constant width 1 touches each side of a regular hexagon of width 1 at precisely one point. Each point of contact determines the one on the opposite side as well, so there is only a 3-parameter space of contact points; call the parameters $\alpha, \beta, \gamma$. Naively, 3 of the points can lie anywhere on their sides of the hexagon, but there’s an additional constraint that no pair of points can be separated by a distance greater than 1, which turns out to confine any pair of the three parameters to a certain intersection of ellipses.

Now, the set $S$ must lie inside the intersection of the six disks of radius 1 centred on the contact points; if we call that intersection of disks $D(\alpha, \beta, \gamma)$, then the union of $D(\alpha, \beta, \gamma)$ over the entire parameter space will give a universal covering. I haven’t checked, but I think that’s probably the entire hexagon.

However, we can do a bit better than that quite easily: the 12-element symmetry group of the hexagon acts on the parameter space of 3-tuples $(\alpha, \beta, \gamma)$, and there’s a natural partition of the parameter space into fundamental domains of that action. So the union of $D(\alpha, \beta, \gamma)$ over a single fundamental domain should also be a universal covering, once you take into account the possibility of applying the symmetries of the hexagon to the set you want to cover, in order to bring the contact points into the fundamental domain.

And the resulting set (which could probably be described analytically quite easily, but so far I’ve only constructed numerically) has an area of about 0.85.

But there might be some clever way to improve it …

I thought that with all the people reading this blog who like constructive mathematics, there would be 50 comments by now. But maybe the language of ‘computable’ mathematics is sufficiently different from that of constructive mathematics that it seems off-putting? (Or maybe my post, where I was thinking out loud about a rather technical issue, was not well crafted to lure people into a discussion.)

Anyway, to me the great ‘miracle’ is the Blaschke selection theorem, which says that the space $\mathcal{C}$ of convex subsets of some ball in $\mathbb{R}^n$, with its Hausdorff metric, is compact. A quick proof is here:

• G. Baley Price, On the completeness of a certain metric space with an application to Blaschke’s selection theorem.

This means that searching through all these convex subsets, which seems initially like a hopeless task, is not so bad if we’re trying to find the maximum value of some continuous function

$$f : \mathcal{C} \to \mathbb{R}$$

The function must be bounded and attain a maximum. What I’m wanting is an effective — that is a computable — version of this result. For this I think it’s enough for $f$ to be sequentially computable and computably uniformly continuous, and for $\mathcal{C}$ to be computably compact — as defined in my blog article.

I just noticed that kind of result could give a rigorous version of Philip Gibbs’ calculation of the number $a$ using simulated annealing. He took a bunch of convex shapes in the plane with diameter 1 and wiggled them around trying to find the convex set of least area that contained all of them. One problem with this strategy is that he couldn’t tell if he’d considered enough shapes to draw a conclusion about all such shapes.

However, if the space of convex shapes of diameter 1 is computably compact, we can find for any $\epsilon$ a finite list of such shapes $x_i$ such that any such shape has Hausdorff distance $\le \epsilon$ from one of these shapes. And then I think we’ll know that any convex set that you can fit all these shapes $x_i$ into will almost hold every shape of diameter 1. Here almost means that they may poke out a distance at most $\epsilon$. And this should be a big step toward rigorously computing the number $a$.

Here’s a possible slight strengthening of “computability structure”: ask that the countable dense subset $X_i$ is computably dense; that is, ask that there be a computable function $H$ such that $$\{ X_i | i \lt H(n)\}$$ is a $\frac{1}{n}$-net. Until someone tells me this is already called something else (or follows from something more natural), I’ll call it “computably generated”.

I initially hoped this would follow from something else natural, (e.g. asking that the identity function should be computable), but I’m starting to despair. For example, I shouldn’t be surprised if there were shufflings of $\mathbb{Q}$ supported on (say) the unit interval, and listed the rationals in $[0,1]$ in such a clumpy way that you’d have to wait for a busy-beaver to finish to get a net of desired fineness.

There are definitely compact metric spaces that can’t be computably generated; For instance, let $\Theta$ be your favourite busy beaver function; then there’s a fine ultrametric on $$\prod_n \{ j \leq \Theta (n) \} ]$$ $$d(x,y) = \frac{1}{1 + min \{ j | x_j \neq y_j \} }$$ but any $\frac{1}{2+k}$-net must have size much larger than $\Theta(k)$. ((Of course, it’s more than possible that we don’t even have a computability structure on this space)).

Anyways, the point of asking for computable generation is that, for a computable-uniformly-continuous function $f$, it should then be possible to compute a finite $\varepsilon$-net that covers each preimage $f^{-1} [ \frac{p}{q} \pm \delta ]$, and contained in $f^{-1} ] \frac{p}{q}\pm 2\delta [$.

Philip, I’m not sure that my approach here leads anywhere useful. So far all I’ve seen is that going to the trouble of shrinking the parameter space to a fundamental domain of the symmetry group can turn out to make no difference at all!

In the mean time, I think I’ve found a simple and rigorously provable reduction of the cover from the paper:

I claim that you can remove the area between the red arc (part of a circle centred on $F_3$) and the two straight edges of the original cover that this arc intersects, $C_3 C_2$ and $C_2 D_1$.

Why? Any curve of constant width 1 that fits inside the original cover must have a pair of points on its boundary that lie on two lines, parallel to the line segments $F_2 F_3$ and $C_2 C_3$, and are a distance of 1 apart. The rightmost point of this pair must lie to the left of $C_2 C_3$, since the whole of triangle C has been removed from the cover, and hence the leftmost point of the pair must lie to the left of $F_3 F_2$.

That means the curve must contain a point in the triangle F. And because the curve has diameter 1, it cannot contain any point whose distance from triangle F is greater than 1. But the region outside the red arc contains only points that are at a greater distance than 1 from any point in triangle F.

Now, crucially, I believe this reduction should be perfectly compatible with Reduction 3 in your paper, where in Case (3) you consider curves that don’t enter the reflected triangles E’ or C’. A mirror-image version of the argument I just gave means that any curve meeting those conditions can’t enter the reflection of the region I’ve just excluded, and hence you can safely reflect such curves without them entering the excluded region. So Reduction 3 still goes through without a hitch.

And all of this argument can be repeated with the area outside the green arc. Together, this leads to a reduction of about $6 \times 10^{-7}$, and brings the upper bound on the cover area down to 0.8441147. And there’s at least one further (very tiny) reduction, since the arc that was originally centred at O in the original cover can also be shifted a small distance along the edge to the point where the red arc meets the edge.

The best way to post pictures here is just to use an HTML img tag referring to a file that you’ve uploaded elsewhere. Or for a large number of images you could just give a link.

I claimed that there’s “at least one further (very tiny) reduction”, since the arc that was centred at O in the original cover can have its centre shifted a small distance along the edge $C_2 D_1$ to the point where the red arc meets that edge.

This turns out to be not so very tiny: it actually more than doubles the reduction, and puts an upper bound on the area of 0.8441140. This is despite it being necessary to increase the slant angle $\sigma$ a tiny bit, in order to keep satisfying the condition that the angle WYQ is larger than a right angle.

If you fix the sign of any single one of the six delta parameters in this diagram:

… then that restricts the region that a curve of constant width 1 inscribed in the hexagon can occupy, to something isometric to this:

In that image I’ve fixed $\delta_1 \ge 0$, but you can get all the other signs and all the other deltas by rotating and or reflecting the same set.

There are three arcs on the boundary here, not just two! The one up the top is the Sprague reduction, the one on the left is the one I argued for here, and the third one, on the right, arises for essentially the same reason as the Sprague reduction: it’s due to the restriction of the point of contact of the curve of constant width to just part of one of the hexagon edges, because of the truncated corner.

Now in this particular case, you can say “so what?” about the third arc, because it lies inside a corner that’s going to be chopped off entirely. But for a general choice of a delta parameter and a sign, that’s not going to be the case, so this third arc need not generally be irrelevant.

I haven’t figured out all the consequences of this, but I’ll see how far I get trying to follow through Philip’s suggestion to break everything down by the signs of the deltas, intersect the sets associated with that choice of signs (imposing the extra restriction $\alpha_1 \le 0$ when $\delta'_1 \ge 0$ and $\delta'_3 \ge 0$), and then take the convex hull of the union of all those intersections.

Ah, we can even go one better, and remove the regions outside four arcs, not three!

This incorporates a second-order effect of a previous truncation: the restriction of the contact point along the top-left edge of the hexagon in turn restricts the contact point along the bottom-right edge, giving us another arc.

And all of this is a flow-on effect of truncating the original bottom-left corner.

Greg, you have made a lot of progress. You are right that you can remove the area outside the arc centred on $F_3$ and use that to improve the area removed around $A$. You can also remove the area outside the arc centred on $B_3$ shown on your diagrams, and there is a third area outside an arc centred on $C_3$ which you must have noticed.

These reductions were already included in my paper http://vixra.org/abs/1401.0219 but the calculations there may not all be accurate. In the joint paper we wanted a simpler clearer proof with no errors so we did not include these reductions. It is good that you have rediscovered them. You are now ready to move onto the next level!

Below are the ten cases that need to be considered distinguished by the signs of the deltas. The red regions show where a curve of constant width does not enter in each case. Triangles $E$ and $C$ are always removed. Every such curve can fit into one of these cases but there are lines of reflection that allow the curves to be transformed. We have to find the best rules for when to reflect (or sometimes rotate) to make a subcover for each case. The union of all ten subcovers will then be a full universal cover.

Each case is a logical puzzle and some are more difficult than others. My best solution used hints from the numerical simulations that more area can be removed near $A$ and near $E_2$ (see figure 26 in the paper) and the area of the best cover I have is 0.844093595. I dont know if it is the best possible but as I said earlier there is also scope for setting lower limits assuming a slanted covering.

Philip wrote here:

… the area of the best cover I have is 0.844093595

Using what ought to be an equivalent approach, the best cover I find has an area of 0.844112132640. This is puzzling, because unless I’ve made a conceptual error or a programming error, this ought to be a lower bound for all covers that can be built simply by choosing signs for the $\delta$ and $\alpha$ parameters.

So at this point I’m not sure if we’re intending to describe exactly the same set, and the discrepancy in areas is due to floating point round-off error, or if we’ve reached different conclusions about the smallest set of this kind that is a universal cover.

To try to resolve this, I’ll describe my calculations in some detail. Philip, please bear with me as I repeat a lot of things that you already know, but I want to try to give an account that’s reasonably self-contained, in case any interested bystander feels like checking it for errors of logic or geometrical reasoning. (It’s probably too much to hope that any third party will leap in and try to reproduce the actual numerical calculations.)

We’re considering curves of constant width 1 that have been translated and rotated to fit inside a regular hexagon of width 1. For each such curve, we can measure six parameters:

The parameters $\alpha_1, \alpha_2, \alpha_3$ measure the distance from the centres of the hexagon’s edges to the points where the curve makes contact with those edges (the red points on the diagram, though the diagram does not include any actual curve). There are only 3 such parameters, rather than 6, because if the curve makes contact with edge $E$ at a certain point $P$, it must make contact with the edge parallel to $E$ at the unique point that is a distance of 1 from $P$.

The $\delta$ parameters relate to two copies of the original hexagon: one that has been rotated counter-clockwise by an angle of $\frac{\pi}{6}+\sigma$ (where for the moment $\sigma$ is a free parameter), and another that is the reflection of that rotated one, in any of the original hexagon’s axes of symmetry. (In the diagram, I’ve used reflection in the blue line to map certain named features to their primed reflections, following the notation in the joint paper. Philip uses a different notation in his diagrams here, giving triangles the same letter, primed, when they intersect, which is probably more sensible … but in any case, in what follows I’ll avoid triangle names and just refer to the $\delta$ parameters on the diagram.)

The parameters $\delta_1, \delta_2, \delta_3$ measure the perpendicular distance from the edges of the rotated hexagon to the two supporting lines for the curve (the dashed lines on the diagram) that are parallel to each pair of those rotated edges. Similarly, the parameters $\delta'_1, \delta'_2, \delta'_3$ measure the same thing for the rotated-and-reflected hexagon.

Now, suppose we’re handed a particular curve of constant width 1, placed inside the hexagon. We measure its nine parameters, which might initially have any of 512 possible 9-tuples of signs. (We’ll be sloppy and just treat 0 as positive by fiat.) However, by rotating and/or reflecting the curve using any of the 12 isometries of the hexagon, we can change the 9 signs and guarantee that they always end up in a smaller set of possibilities than the initial 512.

The advantage of this is seen most dramatically in the choice that was made by Pál (see here, and the linked paper for details), who showed that you can always rotate a curve so that $\delta_1 \gt 0$ and $\delta_3 \gt 0$. If you do that, then the curve will always fit inside a hexagon that has had two corners cut off: the regions where $\delta_1 \lt 0$ and $\delta_3 \lt 0$.

Let’s take it as self-evident that it will always be good to retain Pál’s choice of restrictions (if we didn’t, we’d end up merely making minor tweaks to the full hexagon, having lost the huge reduction of the cover’s area that comes from cutting off two corners). We then have just 128 9-tuples of signs for the parameters, and we can ask what further restrictions are possible.

The 12-element isometry group of the hexagon acts on the set of 9-tuples of signs by moving them on 52 orbits. Some of these orbits will, of course, take the 9-tuples outside the set of 128 defined by Pál’s restriction, so we simply focus on the portions of each orbit that continue to obey that restriction.

If we do this, it turns out that 14 of the 128 9-tuples of signs have just one 9-tuple in their restricted orbit. This means we’re stuck with them. The others fall into 38 orbits of various sizes: 19 of size 2, 2 of size 3, 16 of size 4 and 1 of size 6, which in principle means we have:

$$2^{19} \times 3^2 \times 4^{16} \times 6 = 1.21597189939003392 \times 10^{17}$$

choices for a selection of 52 9-tuples of signs into which we could rotate any curve. Fortunately, it turns out that we don’t need to check anything remotely connected to this terrifying number.

To go further, we need to talk about the specific subsets of the hexagon that will cover any curve that has a restriction on the sign of one of its parameters. If we restrict the sign of a $\delta$ parameter, we get a restricted cover like this:

If we restrict the sign of an $\alpha$ parameter, we get a restricted cover like this:

In these images, arcs of circles of radius 1 that form part of the boundary are marked by drawing dashed lines from their endpoints to the centre of the circle of which they are part.

For the $\delta$-sign restricted cover, it’s obvious that we can cut one corner off the hexagon, but why are there arcs on parts of the boundary? The reason is that if you draw a supporting line $L_C$ for the cover $C$ at any point on its boundary, then a curve of constant width 1 that sits inside the cover will itself have two supporting lines, $L_1$ and $L_2$, a distance of 1 apart, that are parallel to $L_C$. The one closest to $L_C$ must lie on the interior side of $L_C$, in order for the curve to be inside the cover; call that one $L_1$. But this means that $L_2$ must lie a distance of 1 or more away from $L_C$. It then follows that some point of the curve (the point that lies on $L_2$) must lie in the subset of $C$ that is a distance of 1 or more from the line $L_C$; call that subset $C_1$. But since the curve has diameter 1, no point of the curve can lie anywhere in $C$ that is a distance of more than 1 from $C_1$.

For the $\delta$-sign restricted cover, putting a support line along the edge created by the truncation makes $C_1$ into the triangle at the opposite corner of the hexagon. This restricts the cover to points that lie within a circle of radius 1 centred at one corner of that triangle. But as we move the support line around the shape, we get three other arcs as well.

Something similar happens with the $\alpha$-sign restricted cover, except that rather than excising a two-dimensional region, we’ve omitted one half-edge of the hexagon by declaring that no curve can touch it. Putting a support line $L_C$ along the opposite edge gives us a $C_1$ that consists of the non-omitted half-edge, and no point of the curve can lie at a greater distance of 1 from that half-edge. Then as we move the support line around we get the other three arcs.

Depending on the particular parameter number and sign, the restricted covers will just be rotated and/or reflected versions of the two I’ve drawn above (though in the case of the $\delta$ parameters, the covers will also depend on the value of $\sigma$ that’s being used; in the diagrams above I’ve used a huge 12 degrees for the sake of clarity).

To restrict ourselves to any particular 9-tuple of signs, we take the intersections of the appropriate 9 individual restricted covers, one for each parameter. No curve with the nominated 9-tuple of signs for its 9 parameters will lie outside that intersection.

The final task, then, is to choose 52 such 9-tuples of signs, in a way that minimises the area of the convex hull of the union of all 52 9-fold-intersections of restricted covers. This will be a universal cover, because we have chosen one 9-tuple from each of the 52 orbits. Whatever original 9-tuple of signs we have for a curve – which could be anything in the full set of 512 possibilities – there will be some rotation and/or reflection of the hexagon that brings it to one of our chosen 52.

Now, the bad news was that there are, in principle:

$$2^{19} \times 3^2 \times 4^{16} \times 6 = 1.21597189939003392 \times 10^{17}$$

ways to choose a 9-tuple on each orbit. The good news comes if we start by focusing on the 14 9-tuples where we have no choice, because there is only one element in the orbit (subject to the Pál restriction). We can take the 14 associated restricted covers and form the convex hull of their union; we will call this the “compulsory hull” because we have no choice, we must include it.

But the nice surprise that saves us from a combinatorial nightmare is this: if we take the convex hull of the union of this “compulsory hull” with each of the $128-14=114$ restricted covers corresponding to the 9-tuples where we need to make a choice, it turns out that in every orbit but one, there is at least one 9-tuple whose restricted cover is already contained within the compulsory hull. Obviously, then, for those $52-14-1=37$ orbits, we should choose one such 9-tuple … and it will make no difference at all to the final union which such 9-tuple we choose.

That leaves the single orbit with no restricted cover inside the compulsory hull. And this orbit only contains two 9-tuples.

Now, my claim that certain restricted covers were subsets of the compulsory hull is something I checked across a range of angles of interest for $\sigma$, from 0.5 degrees to 1.5 degrees. So anywhere in that range the same logic applies: we will get the minimal area for the final cover by choosing between the two 9-tuples in the sole orbit where we have a meaningful choice to make. So we compute the areas of the final cover for each of these two choices for a range of angles. It turns out that one choice is better across the whole range, and for an angle of $\sigma = 1.0424$ degrees, the smaller cover has a total area of 0.844112132640. It looks like this:

And in fact, this set is exactly the same as the set that’s obtained by making the choices in the joint paper: $\delta_1 \gt 0, \delta_3 \gt 0$ and when $\delta'_1 \gt 0$ and $\delta'_3 \gt 0$ we choose $\alpha_1 \lt 0$. None of the finer-grained decisions about the other four parameters end up offering any further reduction. The only reason the area is slightly less than the area in the joint paper (0.8441153) is that (a) in that paper, not all the regions-outside-arcs that could be removed by restricting the sign of each parameter were removed, and (b) the cover here uses a value for $\sigma$ low enough to cause a certain angle to be less than a right angle, which in the joint paper was ruled out (I guess because it would have complicated the proof).

Philip, your ten diagrams show a representative from each of the ten orbits of the action of the symmetry group on the 6-tuples of $\delta$ parameter signs. But in order to compare covers, could you state explicitly what restrictions you’re imposing on the $\alpha$ parameters in each of these ten cases, and what value you’re using for $\sigma$ for your best cover? That will tell me if we’re talking about the same sets.

Also, if there are further reductions you’re exploiting beyond those shown in the two diagrams I give above, for a restriction on a delta sign and a restriction on an alpha sign, can you explain what they are? If not, we ought to be working with exactly the same sets and doing the same things with them, so we ought to end up agreeing, up to any differences in floating point round-off.

OK, I’ve just realised that there’s at least one potential problem with my analysis here. I was assuming that we could take the restricted covers we get by choosing signs for each parameter, individually, and then simply intersect them to get the restricted cover for curves where we have chosen signs for multiple parameters.

And of course those intersections are covers for the appropriately restricted curves … but they’re not as small as they could be! The various excisions we made from the original sets by running a support line around them won’t necessarily include all the excisions we can make from the intersection. For example:

The set with an outline in red shows the intersection of the nine sets we get when we individually choose the signs of each of the nine parameters to be positive. But if we draw a support line along the lower right-hand truncation that we’ve made in order that $\delta_3 \gt 0$, the line parallel to it a distance of 1 away (the green line in the upper left) defines a portion of the original cover (the small region inside the red set that lies to the left of that green line), within which there must be some point of any curve that fits in the cover. So any part of the cover at a distance greater than 1 from that region (i.e. any part outside the two green arcs) is superfluous.

So I’ll need to go back and redo my whole analysis, taking care to remove as much as possible from each of these sets corresponding to a 9-tuple of signs.

Having used the supporting line method to trim excess regions from the restricted covers for the 9-tuples of parameter signs, I can still only bring the area of the final cover down from my previous value of 0.844112132640 to 0.844112120469, a reduction of about $1.2 \times 10^{-8}$.

Some of the individual restricted covers can be trimmed by quite large amounts: up to an enormous 0.00195152. But the “compulsory hull” of all the restricted covers associated with 9-tuples of sign choices that need to be included in the final cover is only reduced by $1.2 \times 10^{-8}$, hence the final result.

It took me nearly three years to get round to it but here finally is a write-up of how I get the improved upper bound of 0.844093595

An Upper Bound for Lebesgue’s Universal Covering Problem

Hello Greg Egan,

I find your idea of computable function over convex shapes very interesting. I had an idea for such a function and I would be very interested on your feedback. My background is in engineering so I may lack mathematical rigor and tackle the problem more on the algorithmic side.
I emphasize on three assumptions that I cannot prove, hopefully there are sound arguments for those.

Hope you find it interesting

Here it goes:

I. Simulation procedure

Two preliminary (unproven) assumptions:

*Every convex shape of diameter 1 is contained in a shape of constant width 1 (noted CWS)

*Every CWS can be approximated at an arbitrary precision by a CWS with a finite n number of “pinching points” (noted PP) For further information on PPs and an algorithm to construct CWS: http://cgm.cs.mcgill.ca/~athens/cs507/Projects/2001/BB/cs507/

So we focus on CWS with a finite n number of PPs

Trivially, every such shape has an odd number of PPs, and each of the points is at a distance 1 of exactly 2 other PPs, such as we can link them as an arbitrarily shaped star: http://cgm.cs.mcgill.ca/~athens/cs507/Projects/2001/BB/cs507/5.gif

The star we extract from the shape is a graph with exactly 1 cycle. n-3 consecutive angles (by walking the graph) formed at the vertices, entirely characterize the shape. Only n-3 is due to the fact that only N-1 points characterize the shape, as the last one is equidistant to PP1 and PPn-1 and closer to other PPs

So we can encode any shape with n PPs by a n-3 tuple of real numbers each belonging to [0, pi/3] (pi/3 because the only shape which can have a pi/3 angle is trivially the reuleux triangle)

Now for the simulation we just have to iterate with a sufficient precision on all possible tuples in lexical order.

II. Estimation of errors

Three types of errors:

1. Sampling error Error due to sampling when iterating over tuples (missing shapes between chosen values)

2. Left shapes error When having iterated through all shapes with number of PPs <= n, all shapes with PPs > n are left. How well were they approximated by the shapes we already iterated through?

3. Approximation of minimal cover At each step we compute an approximation of a minimal cover for a set of shapes

III. Estimation of computation complexity and optimisation proposals

1: Computation complexity To iterate through all shapes of n points with e precision on angles: (pi/3e)^(n-3) steps. At each step we calculate the minimal coverage by rotating and translating current shape relatively to the others (let’s suppose that this is a constant number of steps)

Which brings us to O((1/e)^n) steps for computing the cover of all shapes with number of PPs <= n

2: Parallel computation

*Unproven assumption (to challenge): The minimal coverage for a finite set of convex shapes has additive structure. For two shapes A and B, we define sum of A and B as the minimal coverage of A and B. We suppose that we have partial associativity: if we have a set S1 of shapes with area > A and another set S2 with area <= A we assume that sum(S1) + sum(S2) = sum(S1 union S2)

We can massively parallelize the computation as addition of independent set of shapes can be done on separate nodes and then aggregated.

I will try to make some simulations as I have most of the code to generate arbitrary shapes already. Keep you posted.