The n-Category Café

Here’s the story:

A subset of the plane has diameter 1 if the distance between any two points in this set is $\le 1$. You know what a circle of diameter 1 looks like. But an equilateral triangle with edges of length 1 also has diameter 1:

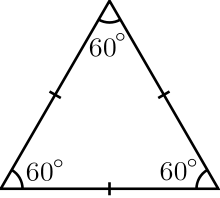
After all, two points in this triangle are farthest apart when they’re at two corners.

Note that this triangle doesn’t fit inside a circle of diameter 1:

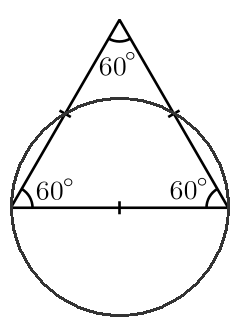
There are lots of sets of diameter 1, so it’s interesting to look for a set that can contain them all.

In 1914, the famous mathematician Henri Lebesgue sent a letter to a pal named Pál. And in this letter he challenged Pál to find the convex set with smallest possible area such that every set of diameter 1 fits inside.

More precisely, he defined a universal covering to be a convex subset of the plane that can cover a translated, reflected and/or rotated version of every subset of the plane with diameter 1. And his challenge was to find the universal covering with the least area.

Pál worked on this problem, and 6 years later he published a paper on it. He found a very nice universal covering: a regular hexagon in which one can inscribe a circle of diameter 1. This has area

$$\frac{\sqrt{3}}{2} = 0.86602540 \dots$$

But he also found a universal covering with less area, by removing two triangles from this hexagon—for example, the triangles C₁C₂C₃ and E₁E₂E₃ here:

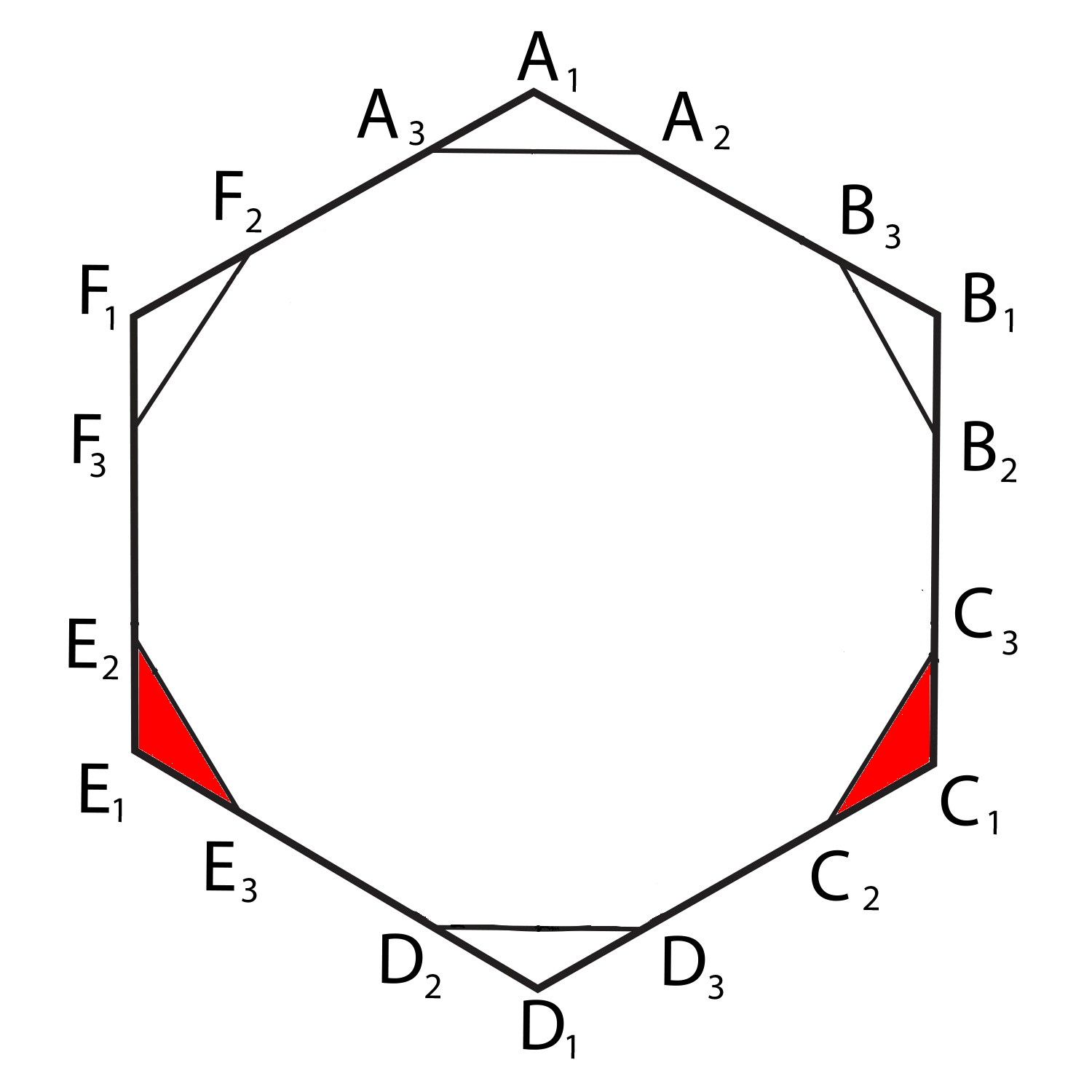
Our paper explains why you can remove these triangles, assuming the hexagon was a universal covering in the first place. The resulting universal covering has area

$$2 - \frac{2}{\sqrt{3}} = 0.84529946 \dots$$

In 1936, Sprague went on to prove that more area could be removed from another corner of Pál’s original hexagon, giving a universal covering of area

$$0.8441377708435 \dots$$

In 1992, Hansen took these reductions even further by removing two more pieces from Pál’s hexagon. Each piece is a thin sliver bounded by two straight lines and an arc. The first piece is tiny. The second is downright microscopic!

Hansen claimed the areas of these regions were $4 \cdot 10^{-11}$ and $6 \cdot 10^{-18}$. However, our paper redoes his calculation and shows that the second number is seriously wrong. The actual areas are $3.7507 \cdot 10^{-11}$ and $8.4460 \cdot 10^{-21}$.

Philip Gibbs has created a Java applet illustrating Hansen’s universal cover. I urge you to take a look! You can zoom in and see the regions he removed:

• Philip Gibbs, Lebesgue’s universal covering problem.

I find that my laptop, a Windows machine, makes it hard to view Java applets because they’re a security risk. I promise this one is safe! To be able to view it, I had to go to the “Search programs and files” window, find the “Configure Java” program, go to “Security”, and add

http://gcsealgebra.uk/lebesgue/hansen

to the “Exception Site List”. It’s easy once you know what to do.

And it’s worth it, because only the ability to zoom lets you get a sense of the puny slivers that Hansen removed! One is the region XE₂T here, and the other is T′C₃V:

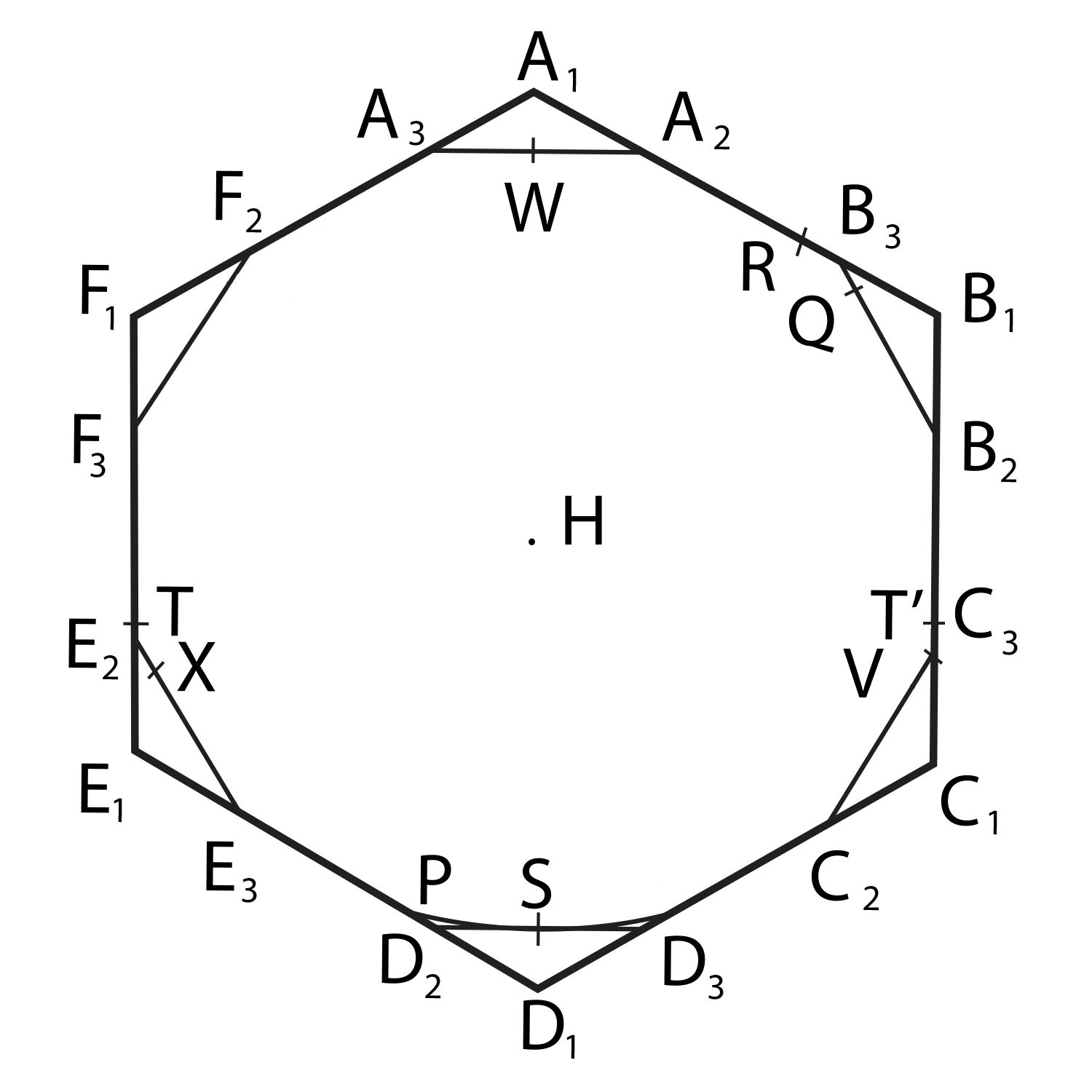
You can use this picture to help you find these regions in Philip Gibbs’ applet. But this picture is not in scale! In fact the smaller region, T′C₃V, has length $3.7 \cdot 10^{-7}$ and maximum width $1.4 \cdot 10^{-14}$, tapering down to a very sharp point.

That’s about a few atoms wide if you draw the whole hexagon on paper! And it’s about 30 million times longer than it is wide. This is the sort of thing you can only draw with the help of a computer.

Anyway, Hansen’s best universal covering had an area of

$$0.844137708416 \dots$$

This tiny improvement over Sprague’s work led Klee and Wagon to write:

it does seem safe to guess that progress on [this problem], which has been painfully slow in the past, may be even more painfully slow in the future.

However, our new universal covering removes about a million times more area than Hansen’s larger region: a whopping $2.233 \cdot 10^{-5}$. So, we get a universal covering with area

$$0.844115376859 \dots$$

The key is to slightly rotate the dodecagon shown in the above pictures, and then use the ideas of Pál and Sprague.

There’s a lot of room between our number and the best lower bound on this problem, due to Brass and Sharifi:

$$0.832$$

So, one way or another, we can expect a lot of progress now that computers are being brought to bear. Philip Gibbs has a heuristic computer calculation pointing toward a value of

$$0.84408$$

so perhaps that’s what we should shoot for.

Read our paper for the details! If you want to check our work, we’ll be glad to answer lots of detailed questions. We want to rotate the dodecagon by an amount that minimizes the area of the universal covering we get, so we use a program to compute the area for many choices of rotation angle:

• Philip Gibbs, Java program.

The program is not very long—please study it or write your own, in your own favorite language! The output is here:

• Philip Gibbs, Java program output.

and as explained at the end of our paper, the best rotation angle is about $1.3^\circ$.