Configurations of Lines and Models of Lie Algebras (Part 2)
Posted by John Baez
To get deeper into this paper:
- Laurent Manivel, Configurations of lines and models of Lie algebras.
we should think about the 24-cell, the Dynkin diagram, and the Lie algebra that it describes. After all, its this stuff that underlies the octonions, which in turn underlies the exceptional Lie algebras, which are the main subject of Manivel’s paper.
Remember that the root lattice of is called the lattice: it consists of vectors in with integer entries that sum to an even number.
I’m interested in so I’m interested in the root lattice: 4-tuples of integers that sum to an even number! If you like the Hurwitz integral quaternions these are essentially the same thing multiplied by a factor of 2.
The shortest nonzero vectors in the lattice are the roots. There are 16 like this:
and 8 like this:
The roots form the vertices of a regular polytope in 4 dimensions. It’s called the 24-cell because it not only has 24 vertices, it also has 24 octahedral faces: it’s self-dual.
One thing we’re seeing here is that we can take the vertices of a 4-dimensional cube, namely :
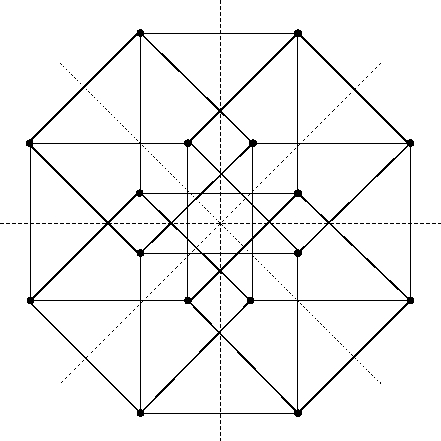
and the vertices of a 4-dimensional orthoplex, namely and permutations:
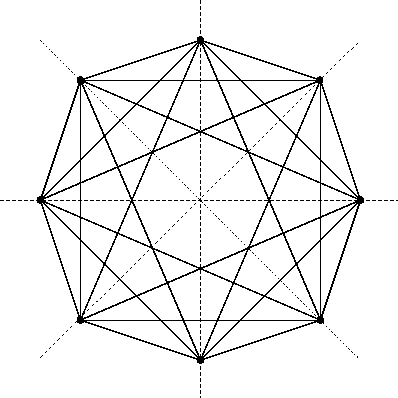
and together they form the vertices of a 24-cell:

(In case you forgot, an orthoplex or cross-polytope is the -dimensional analogue of an octahedron, a regular polytope with vertices.)
However, we can go further! If you take every other vertex of an -dimensional cube — that is, start with one vertex and then all its second nearest neighbors and their second nearest neighbors and so on — you get the vertices of something called the -dimensional demicube. In 3 dimensions, a demicube is a regular tetrahedron, so you can fit two tetrahedra in a cube like this:

But in 4 dimensions, a demicube is an orthoplex! This is easy to see: if we take these points
and keep only those with an even number of minus signs, we get
which are the 8 vertices of an orthoplex.
So, we can take the vertices of a 24-cell and partition them into three 8-element sets, each being the vertices of an orthoplex!
And this has a nice representation-theoretic significance:
the vertices of the first orthoplex correspond to the weights of the 8-dimensional vector representation of ;
the vertices of the second correspond to the weights of the 8-dimensional left-handed spinor representation of ;
the vertices of the third correspond to the weights of the 8-dimensional right-handed spinor representation of
Here I’m being a bit sneaky, identifying the weight lattice of with the root lattice. In fact it’s twice as dense, but it ‘looks the same’: it’s the same up to a rescaling and rotation. The weight lattice contains a 24-cell whose vertices are the weights of the vector, left- and right-handed spinor representations. But the root lattice, which is what I really had been talking about, contains a larger 24-cell whose vertices are the roots — that is, the nonzero weights of the adjoint representation of on itself.
Now, you may wonder which is the ‘first’ orthoplex, which is the ‘second’ one and which is the ‘third’, but it doesn’t matter much since there’s a symmetry between them! This is triality. The group acts on as outer automorphisms, and thus on the weight lattice and root lattice. So, it acts as symmetries of the 24-cell — and it acts by permuting the 3 orthoplexes!
But here’s the cool thing that Manivel focuses on. Suppose we take the 24-cell whose vertices are the roots of . Any orthoplex in here consists of 4 pairs of opposite roots along 4 orthogonal axes. So, it gives a root system of type . In other words, it picks out a copy of in .
This Lie subalgebra
acts on by the adjoint action. It acts on itself, and it acts on the rest of via the representation
where each copy of acts on just one factor of (in the obvious way). The weights of this ‘rest of’ form the vertices of a 4-dimensional cube.
So, we’re getting a nice vector space isomorphism
which is based on how the vertices of a 24-cell can be partitioned into the vertices of an orthoplex and a cube. But in fact we’re getting 3 such isomorphisms, related by triality!
If we call the 4 copies of here , we can write
Also, we can write the three 8-dimensional irreducible representations of as
Note that they come from the three ways of partitioning a 4-element set into two 3-element sets.
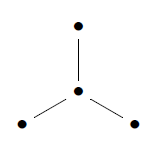
Manivel calls this description of the four-ality description, but I prefer to speak of tetrality. How is tetrality related to triality? The Dynkin diagram of has symmetry, which yields triality:
But the corresponding extended or affine Dynkin diagram has symmetry, which yields tetrality:
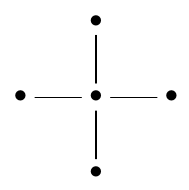
One reason the affine Dynkin diagram is important is that maximal-rank Lie subalgebras of a Lie algebra with Dynkin diagram are obtained by deleting a dot from the corresponding affine Dynkin diagram . If we delete the middle dot of we get a disconnected diagram with 4 separate dots, which is the diagram for . This is why shows up as a maximal rank Lie subalgebra of .
The relation between tetrality and triality, I believe, is that there’s a homomorphism coming from the 3 ways of partitioning a 4-element set into 2-element sets.
This is a good place to stop, though we’re really just getting started.


Re: Configurations of Lines and Models of Lie Algebras (Part 2)
Just because the very-symmetric 24-cell left me scratching my head — not everything that looks like a square is a square.