Topological Crystals (Part 2)
Posted by John Baez
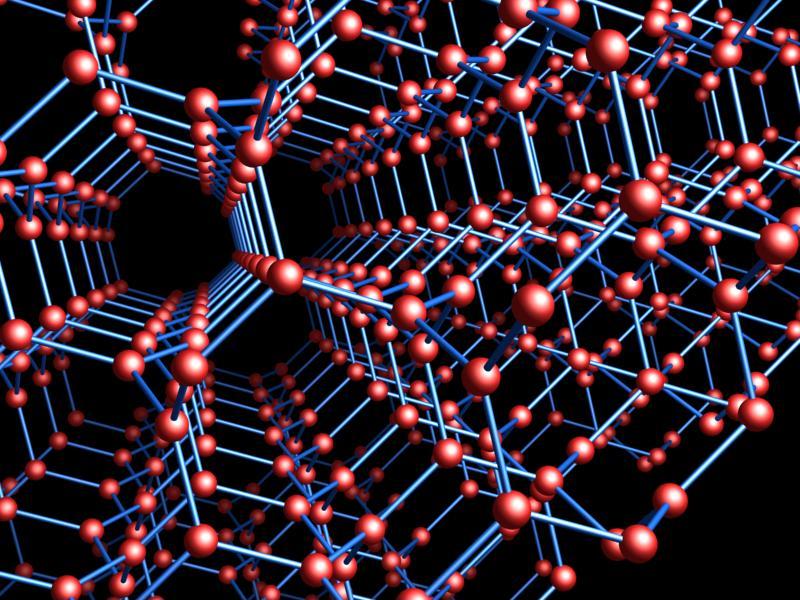
We’re building crystals, like diamonds, purely from topology. Last time I said how: you take a graph and embed its maximal abelian cover into the vector space .
Now let me back up and say a bit more about the maximal abelian cover. It’s not nearly as famous as the universal cover, but it’s very nice.
The basic idea
By ‘space’ let me mean a connected topological space that’s locally nice. The basic idea is that if is some space, its universal cover is a covering space of that covers all other covering spaces of . The maximal abelian cover has a similar universal property — but it’s abelian, and it covers all abelian connected covers. A cover is abelian if its group of deck transformations is abelian.
The cool part is that universal covers are to homotopy theory as maximal abelian covers are to homology theory.
What do I mean by that? For starters, points in are just homotopy classes of paths in starting at some chosen basepoint. And the points in are just ‘homology classes’ of paths starting at the basepoint.
But people don’t talk so much about ‘homology classes’ of paths. So what do I mean by that? Here a bit of category theory comes in handy. Homotopy classes of paths in are morphisms in the fundamental groupoid of . Homology classes of paths are morphisms in the abelianized fundamental groupoid!
But wait a minute — what does that mean? Well, we can abelianize any groupoid by imposing the relations
whenever it makes sense to do so. It makes sense to do so when you can compose the morphisms and in either order, and the resulting morphisms and have the same source and the same target. And if you work out what that means, you’ll see it means .
But now let me say it all much more slowly, for people who want a more relaxed treatment. After all, this is a nice little bit of topology that could be in an elementary course!
The details
There are lots of slightly different things called ‘graphs’ in mathematics, but in topological crystallography it’s convenient to work with one that you’ve probably never seen before. This kind of graph has two copies of each edge, one pointing in each direction.
So, we’ll say a graph has a set of vertices, a set of edges, maps assigning to each edge its source and target, and a map sending each edge to its inverse, obeying
and
for all .
That inequality at the end will make category theorists gag: definitions should say what’s true, not what’s not true. But category theorists should be able to see what’s really going on here, so I leave that as a puzzle.
For ordinary folks, let me repeat the definition using more words. If and we write , and draw as an interval with an arrow on it pointing from to . We write as , and draw as the same interval as , but with its arrow reversed. The equations obeyed by say that taking the inverse of gives an edge and that . No edge can be its own inverse.
A map of graphs, say , is a pair of functions, one sending vertices to vertices and one sending edges to edges, that preserve the source, target and inverse maps. By abuse of notation we call both of these functions .
I started out talking about topology; now I’m treating graphs very combinatorially, but we can bring the topology back in.
From a graph we can build a topological space called its geometric realization. We do this by taking one point for each vertex and gluing on one copy of for each edge , gluing the point to and the point to , and then identifying the interval for each edge with the interval for its inverse by means of the map . Any map of graphs gives rise to a continuous map between their geometric realizations, and we say a map of graphs is a cover if this continuous map is a covering map. For simplicity we denote the fundamental group of by , and similarly for other topological invariants of . However, sometimes I’ll need to distinguish between a graph and its geometric realization .
Any connected graph has a universal cover, meaning a connected cover
that covers every other connected cover. The geometric realization of is connected and simply connected. The fundamental group acts as deck transformations of , meaning invertible maps such that . We can take the quotient of by the action of any subgroup and get a cover .
In particular, if we take to be the commutator subgroup of , we call the graph the maximal abelian cover of the graph , and denote it by . We obtain a cover
whose group of deck transformations is the abelianization of . This is just the first homology group . In particular, if the space corresponding to has holes, this is a free abelian group on generators.
I want a concrete description of the maximal abelian cover! I’ll build it starting with the universal cover, but first we need some preliminaries on paths in graphs.
Given vertices in , define a path from to to be a word of edges with for some vertices with and . We allow the word to be empty if and only if ; this gives the trivial path from to itself. Given a path from to we write , and we write the trivial path from to itself as . We define the composite of paths and via concatenation of words, obtaining a path we call . We call a path from a vertex to itself a loop based at .
We say two paths from to are homotopic if one can be obtained from the other by repeatedly introducing or deleting subwords of the form where . If is a homotopy class of paths from to , we write . We can compose homotopy classes and by setting .
If is a connected graph, we can describe the universal cover as follows. Fix a vertex of , which we call the basepoint. The vertices of are defined to be the homotopy classes of paths where is arbitrary. The edges in from the vertex to the vertex are defined to be the edges with . In fact, there is always at most one such edge. There is an obvious map of graphs
sending each vertex of to the vertex of . This map is a cover.
Now we are ready to construct the maximal abelian cover . For this, we impose a further equivalence relation on paths, which is designed to make composition commutative whenever possible. However, we need to be careful. If and , the composites and are both well-defined if and only if and . In this case, and share the same starting point and share the same ending point if and only if and . If all four of these equations hold, both and are loops based at . So, we shall impose the relation only in this case.
We say two paths are homologous if one can be obtained from another by:
repeatedly introducing or deleting subwords where , and/or
repeatedly replacing subwords of the form by those of the form , where and are loops based at the same vertex.
My use of the term ‘homologous’ is a bit nonstandard here!
We denote the homology class of a path by . Note that if two paths , are homologous then and . Thus, the starting and ending points of a homology class of paths are well-defined, and given any path we write . The composite of homology classes is also well-defined if we set .
We construct the maximal abelian cover of a connected graph just as we constructed its universal cover, but using homology classes rather than homotopy classes of paths. And now I’ll introduce some jargon that should make you start thinking about crystals!
Fix a basepoint for . The vertices of , or atoms, are defined to be the homology classes of paths where is arbitrary. Any edge of , or bond, goes from some atom to the some atom . The bonds from to are defined to be the edges with . There is at most one bond between any two atoms. Again we have a covering map
The homotopy classes of loops based at form a group, with composition as the group operation. This is the fundamental group of the graph . (It depends on the basepoint , but I’ll leave that out out of the notation just to scandalize my colleagues. It’s so easy to live dangerously when you’re an academic!)
Now, this fundamental group is isomorphic to the usual fundamental group of the space associated to . By our construction of the universal cover, is also the set of vertices of that are mapped to by . Furthermore, any element defines a deck transformation of that sends each vertex to the vertex .
Similarly, the homology classes of loops based at form a group with composition as the group operation. Since the additional relation used to define homology classes is precisely that needed to make composition of homology classes of loops commutative, this group is the abelianization of . It is therefore isomorphic to the first homology group of the geometric realization of !
By our construction of the maximal abelian cover, is also the set of vertices of that are mapped to by . Furthermore, any element defines a deck transformation of that sends each vertex to the vertex .
So, it all works out! The fundamental group acts as deck transformations of the universal cover, while the first homology group acts as deck transformations of the maximal abelian cover!
Puzzle for experts: what does this remind you of in Galois theory?
We’ll get back to crystals next time.

Re: Topological Crystals (Part 2)
I guess by Hurewicz that something like this will works only for the first nonzero homotopy group. Do you have a version for other homology groups? Abelianization isn’t going to be obviously helpful any more.
(Stupid, basic question: is ordinary homology representable? I know ordinary cohomology is representable, by Eilenberg-Mac Lane spaces, so I’m sure I should know this.)