The n-Category Café

Throughout this paper, Kelly works in the enriched context. Where normally we like to think of there being a set of arrows between any two objects of a category, Kelly wants us to think of there being an object of arrows. This object of arrows can live in any suitably nice category, which here will mean a symmetric monoidal closed and cocomplete (and later, locally finitely presentable) category. We call this category our base category, and denote it by the letter $\mathcal{V}$.

For the rest of this blog post, we will work from the $\mathcal{V}$-point of view. When I say “category”, I will mean $\mathcal{V}$-category, and same for “functor” and “natural transformation”. For the most part, this will work smoothly. But the crucial notion of being “filtered”, which we will come to later, is only defined over the category of sets. I’ll try and be explicit about this when it comes up. For a brief intro to the $\mathcal{V}$-point of view, see the previous blog post which introduces enrichment and its limits.

Understanding Objects by Looking at Figures in Them

When we work with a mathematical structure $X$, we often like to do so in terms of its elements. In our base category, it suffices to look at the points of $X$, the maps $1 \to X$. But, in more general categories $\mathcal{C}$, we may need to consider figures $S \to X$ of a more general shape.

Remark For the rest of this post, I will use the term “figure in $X$” to mean a morphism $S \to X$ in a category, and “shape” to mean the domain of a figure. By an “incidence relation” between shapes, I just mean morphisms between them. A somewhat more common name for “shape” would be “test space”, but I find the word “shape” to be more cozy.

Yoneda’s lemma tells us that we lose no information if we use figures of an arbitrary shape.

Lemma (Yoneda’s Lemma) In any category, morphisms $X \to Y$ naturally correspond to functions which take figures in $X$ to figures of the same shape in $Y$ which respect the incidence relations between the shapes.

However, it will often be the case that general shapes are just too complicated to work with. After all, we are trying to study an object in a category; a general morphism into it can be no less complicated. Even worse, there are often so many general shapes that they cannot be collected into a set (if we are working in a large category). It would be very nice to have a small subcategory $\mathcal{G} \hookrightarrow \mathcal{C}$ of “tractable shapes” that we could restrict our attention to. “Tractable” is not a technical term, but more of a suggestive name like “nice”.

Such a subcategory would induce a functor $\mathcal{C}(\mathcal{G}, -) : \mathcal{C} \to \mathcal{V}^{\mathcal{G}^{\text{op}}}$ sending an object of $\mathcal{C}$ to its functor of “figures with tractable shape”. If we can glue together the objects of $\mathcal{C}$ (that is, if $\mathcal{C}$ is cocomplete), then this functor will have a left adjoint given by taking the weighted colimit of the inclusion $\mathcal{G} \hookrightarrow \mathcal{C}$. We can think of this left adjoint as gluing together a bunch of tractable shapes into an object of $\mathcal{C}$. Let’s look at a few examples of this kind of arrangement.

• As I mentioned above, it suffices to work with points (that is, figures $1 \to X$ of shape $1$) when we are in the base category. This should mean that if we take our category of “tractable shapes” to be just the subcategory containing the monoidal unit $1$, we will recover all of our base category. And indeed, $\mathcal{V}(1, -) : \mathcal{V} \to \mathcal{V}^{1^{\text{op}}}$ is an isomorphism of categories! Its inverse sends an object $W : 1^{\text{op}} \to \mathcal{V}$ of points to the copower $W \cdot 1$, the $W$-indexed sum of points.
• Let’s work over sets, and consider the category of graphs $\mathcal{C}$ (to be specific, by “graph” I mean a symmetric relation). It no longer suffices to just look at points $\ast \to X$ (figures in $X$ whose shape is a single point $\ast$), since there can be many graphs with the same set of points. Nor can we just look at figures whose shape is a single edge $\ast - \ast$, since many graphs have the same set of edges. But if we keep in mind the incidence relations between these two shapes, which is just that the point $\ast$ lies in the edge $\ast - \ast$ in two ways, then we can recover the whole of our graph $X$. We let $\mathcal{G} = \{\ast \rightrightarrows (\ast - \ast) \}$ be our subcategory of tractable shapes, and we find that $\mathcal{C}(\mathcal{G}, -) ; \mathcal{C} \to \mathcal{V}^{\mathcal{G}^{\text{op}}}$ is fully faithful. Its adjoint is the functor which glues a bunch of edges onto a bunch of points, and that it is fully faithful means that any morphism of graphs is determined by its actions on the points and edges.
• Now let’s look at an example where our object $X$ is seriously intractable. Working over sets again, let $\mathcal{C}$ be the category of topological spaces. As above, a topological space $X$ is not determined by its points. We can try to get a grip on $X$ by modeling it with triangles. Higher dimensional triangles are called simplices, and they are particularly nice spaces, so we can take our tractable objects $\mathcal{G}$ to be the subcategory of simplices and their incidence relations. Then the $\mathcal{C}(\mathcal{G}, -) : \mathcal{C} \to \mathcal{V}^{\mathcal{G}^{\text{op}}}$ sends a topological space to its singular simplicial set, and its left adjoint gives the geometric realization of an abstract simplicial set. In this case, $\mathcal{C}(\mathcal{G}, -)$ is only faithful; there are spaces (like Cantor’s space) which aren’t well studied by looking at triangles in them.

For this program of looking at “tractable shapes” to work out, we will need the objects of $\mathcal{C}$ to be suitably determined by the figures of tractable shape inside them. We will take “suitably determined” to mean that we can test if a morphism is an isomorphism by checking if it induces a bijection on figures of tractable shape.

Definition Let $\mathcal{C}$ be cocomplete and let $\mathcal{G} \hookrightarrow \mathcal{C}$ be a subcategory. We say that $\mathcal{G}$ is a strong generator of $\mathcal{C}$ if $\mathcal{C}(\mathcal{G}, -)$ is conservative (that is, if it reflects isomorphisms).

So, we are looking for a strong generator $\mathcal{G}$ consisting of “tractable” objects of $\mathcal{C}$. But what does “tractable” mean?

Let’s consider an algebraic example, say, the category $\mathcal{C} = \text{Grp}$ of groups (as a set-category). We often study algebras by looking at the equations that elements in them satisfy. For example, a group is abelian if $ab = ba$ for every two elements $a$ and $b$ in it. These finite sets of relations between elements can be seen as figures in the group; the shape of these figures is a finitely presented group, generated by the elements and quotiented by the relations in question. For example, the commuting pairs in a group are precisely the figures (homomorphisms) of shape (with domain) $\langle a, b \mid ab = ba \rangle$.

In this algebraic setting, it seems reasonable to take “tractable” to mean finitely presentable. By finitely presentable, I mean admitting a finite presentation in terms of generators and relations in the usual sense. Here is a categorical way to describe a presentation in terms of generators and relations: we have a set of generators and a set of relations together with two homomorphisms from the free algebra on the relations to the free algebra on the generators taking a relation to the left and right hand sides of the equality that represents it. Then, to be presented by such a presentation means to be a coequalizer of those two arrows. For example, the group $\langle a, b \mid ab = ba\rangle$ above is given by the coequalizer of $\langle c \rangle \rightrightarrows \langle a , b \rangle$ where the left arrow sends $c$ to $ab$ and the right sends $c$ to $ba$.

Interestingly, there is an abstract categorical definition of finite presentability which doesn’t mention generators or relations at all!

Theorem In a category of algebras $\mathcal{C}$ (say, models of a Lawvere theory), an algebra $A$ is finitely presentable if and only if the hom functor $\mathcal{C}(A, -)$ commutes with filtered colimits.

Finite Shapes and Gluing Them Together

Given the above abstract definition of finite presentability, we will take “tractable” to mean “finitely presentable” in the abstract categorical sense. Let’s explain precisely what this is now.

Definition A set-category $\mathcal{D}$ is filtered if every functor $\mathcal{J} \to \mathcal{D}$ with $\mathcal{J}$ finite has a cocone.

The colimit of a diagram $\mathcal{D} \to \mathcal{C}$ is filtered if $\mathcal{D}$ is.

A functor $\mathcal{C} \to \mathcal{B}$ is finitary if it commutes with filtered colimits.

An object $G$ in $\mathcal{C}$ is finitely presentable (or f.p.) if $\mathcal{C}(G, -) : \mathcal{C} \to \mathcal{V}$ is finitary. We denote by $\mathcal{C}_f$ the (full) category of f.p. objects in $\mathcal{C}$.

Finitely presentable objects are “morally finite”, relative to whatever category they are in. A good grounding example occurs in the truth value enriched setting.

Theorem Let $\Omega$ be the order of open sets in a topological space $X$, considered as a category over the truth values. If $K \subseteq X$ is a subset, then the functor $U \mapsto K \subseteq U$ is finitary if and only if $K$ is compact.

Proof Commuting with filtered colimits means $$K \subseteq \bigcup_i U_i \iff \exists i (K \subseteq U_i)$$ for each filtered family of open sets $(U_i)_i$. We can complete any open cover to a filtered cover by throwing in finite unions of opens in the cover; if the functor is finitary, then one such finite union contains $K$, so $K$ is compact.

If $K$ is compact, any open cover (including one that is filtered) contains a finite subcover; since the cover is filtered, there is open set in it containing the finite cover, which shows that the functor is finitary.

It’s reasonable to think of compact sets as “topologically finite”. Representing a finitary functor makes an object “finite” in the category in question. For example, a finitely presentable set is finite.

Claim A finitely presentable set is finite.

Proof If $X$ is finitely presentable, then $\text{Set}(X,-)$ commutes with filtered colimits. Every set is the filtered colimit of its finite subsets, so in particular $\text{Set}(X,X) \cong \text{colim}\text{Set}(X, n)$. But then the identity of $X$ factors through one of its finite subsets, so $X$ is finite.

It would be good to show further that every finite set is finitely presentable. We can do even better by showing that gluing together finitely many finite shapes gives us a finite shape. But first, we should make sure we know what “finitely many” means in the enriched context.

Definition A weight $W : \mathcal{D} \to \mathcal{V}$ is finite when

• $\mathcal{D}$ has finitely many objects (up to isomorphism),
• $\mathcal{D}(i, j)$ is f.p. for all $i$ and $j$ in $\mathcal{D}$, and
• $W_i$ is f.p. for all $i$ in $\mathcal{D}$.

Finite (co)limits are those whose weights are finite.

Lemma (4.41) For $\mathcal{C}$ cocomplete, $\mathcal{C}_f$ is closed under finite colimits.

Corollary A set is finite if and only if it is finitely presentable.

Proof We saw that finitely presentable sets are finite, so it remains to show that finite sets are finitely presentable. But a finite set is a finite coproduct of the set $1$, and $1$ is finitely presentable because $\text{Set}(1, X) \cong X$ commutes with filtered colimits.

Now that we have a good formal definition of “tractable”, we can define those categories whose objects are suitably determined by the tractable figures within them.

Definition A category $\mathcal{C}$ is locally finitely presentable (l.f.p.) when

• it is cocomplete, and
• there is a small subcategory $\mathcal{G} \hookrightarrow \mathcal{C}$ so that the induced $\mathcal{C}(\mathcal{G}, -)$ is finitary and conservative.

Note that $\mathcal{C}(\mathcal{G}, -)$ being finitary implies that $\mathcal{G} \hookrightarrow \mathcal{C}_f$, since we can calculate colimits in $\mathcal{V}^{\mathcal{G}^{\text{op}}}$ pointwise.

Since being finitary relies on a definition over the category of sets, there can be subtle differences between the objects which are finitely presented over sets versus objects that are finitely presented over the base $\mathcal{V}$. For example, the monoidal unit $1$ is always finitely presentable over $\mathcal{V}$, since $\mathcal{V}(1, X) \cong X$. But over sets, it might not be, since the set of points of an object in $\mathcal{V}$ might be ill-behaved. Kelly gives a good example of this: in the category of actions of a group $G$, the monoidal unit $G$ is always finitely presentable over the actions, but it is only finitely presentable over sets if $G$ is finite.

For more on these subtleties, see section 5 of the paper; from now on, we will assume that our base $\mathcal{V}$ is l.f.p. over sets and that moreover the f.p. objects in $\mathcal{V}$ are the same whether taken over $\mathcal{V}$ or over sets. This occurs if and only if the monoidal unit of $\mathcal{V}$ is f.p. over sets and the tensor product of two f.p.-over-sets objects is f.p. over sets (see 5.5 in the paper). Kelly calls this situation being “l.f.p. as a monoidal closed category”, and so we will as well.

Now, Kelly proves some serious theorems about l.f.p. categories.

Theorem (7.2) Let $\mathcal{C}$ be l.f.p. with strong generator $\mathcal{G} \hookrightarrow \mathcal{C}_f$. Then

• $\mathcal{C}_f$ is the closure of $\mathcal{G}$ under finite colimits,
• $\mathcal{C}_f$ is dense in $\mathcal{C}$, meaning that $\mathcal{C}(\mathcal{C}_f,-)$ is fully faithful.
• $\mathcal{C}(\mathcal{C}_f, -)$ is also finitary.
• $\mathcal{C}$ is complete.

This theorem shows that the finite shapes in a category whose objects are determined by some particular subcategory $\mathcal{G}$ of finite “tractable” shapes are precisely those shapes which can be glued together out of finitely many “tractable” shapes from $\mathcal{G}$. For example, working over sets, we see that the finitely presentable graphs are precisely the finite colimits of the point and the edge, that is, precisely the finite graphs. We can also deduce that the finitely presentable simplicial sets are those which have a finite number of simplices.

Rather surprisingly, we also find that $\mathcal{C}$ is complete. Perhaps this is not so surprising though; if we know how to glue our objects together out of finite shapes, then we can form families of objects by forming families of these shapes. So, l.f.p. categories are very nice categories indeed. As a corollary of this theorem, Kelly gives a few more characterizations of l.f.p. categories that show that the choice of generators $\mathcal{G}$ is not essential.

Corollary (7.3) The following are equivalent for a cocomplete category $\mathcal{C}$:

• $\mathcal{C}$ is locally finitely presentable,
• $\mathcal{C}_f$ is small and strongly generating,
• $\mathcal{C}_f$ is small and dense,
• $\mathcal{C}$ is a reflective subcategory of $\mathcal{V}^{\mathcal{G}^{\text{op}}}$ with finitary inclusion, for some $\mathcal{G}$.

Here we see that the l.f.p. categories are reflective subcategories of presheaf categories. Since presheaf categories are always fantastically nice (inheriting, as they do, most of the nice structure of the base), l.f.p. categories are fantastically nice as well. For example, in the category of sets, finite limits commute with filtered colimits. In a l.f.p. category over an l.f.p. base, we can deduce the same.

Lemma (4.9) Let $\mathcal{C}$ be a l.f.p. category over an l.f.p. (as a monoidal closed category) base. Then finite limits commute with filtered colimits in $\mathcal{C}$.

Furthermore, l.f.p. categories satisfy two really nice adjoint functor theorems. Before we can express them, we need to mention that the above discussion of filtered colimits and f.p. objects can be repeated with “finite” (that is, “less than $\aleph_0$”) being replaced by “less than $\kappa$” for any regular cardinal $\kappa$.

Theorem (7.8, 7.9) Let $\mathcal{C}$ and $\mathcal{B}$ be l.f.p. and let $F : \mathcal{C} \to \mathcal{B}$ be a functor. Then

• $F$ is a left adjoint if and only if it commutes with colimits, and
• $F$ is a right adjoint if and only if it and commutes with limits and $\kappa$-filtered colimits for some regular cardinal $\kappa$.

As an example, let $\mathcal{C}$ be the category of graphs over sets, and let $F = \mathcal{C}(\ast, -)$ be the functor of points. As a covariant representable, $F$ commutes with limits, and since colimits of graphs are constructed pointwise, it also commutes with colimits. Therefore, $F$ has both a left and a right adjoint, given by forming the discrete graph with no edges and the complete graph with all possible edges.

An Aside: Essentially Algebraic Theories

As an aside, let’s discuss the notion of an essentially algebraic theory. A theory is algebraic when it involves equations between functions of finitely many variables, and therefore may be interpreted in any category with finite products. A theory is essentially algebraic when it involves equations between partial functions of finitely many variables (whose domains are carved out by equations). Therefore, an essentially algebraic theory may be interpreted in any category with finite limits. The theory of categories is an example of an essentially algebraic theory which is not algebraic; composition is only defined for some pairs of morphisms.

Definition An essentially algebraic theory $\mathcal{T}$ is a small finitely complete category.

A model of an essentially algebraic theory $\mathcal{T}$ is a left exact functor $M : \mathcal{T} \to \mathcal{C}$. Being left exact (or, shortly, lex) means commuting with finite limits.

A moral of this story is that a lot of what works for Lawvere theories over sets works for enriched essentially algebraic theories. In particular, we can take the free finite completion $\mathcal{L}_{\mathcal{C}}$ of a category $\mathcal{C}$, which by definition satisfies the following universal property: $$\text{Lex}(\mathcal{L}_{\mathcal{C}}, \mathcal{B}) \simeq \mathcal{V}\text{-Cat}(\mathcal{C}, \mathcal{B})$$ for f.c. $\mathcal{B}$. In particular, $\mathcal{L}_1 \cong \mathcal{V}_f^{\text{op}}$, so we see that $$\text{Lex}(\mathcal{V}_f^{\text{op}}, \mathcal{V}) \simeq \mathcal{V}\text{-Cat}(1, \mathcal{B}) \cong \mathcal{B}.$$ Therefore, we can see $\mathcal{V}_f^{\text{op}}$ as the “theory of an object”; its models are just objects.

An algebra of an essentially algebraic theory is a model in the base category. Kelly gives the following characterization of algebras of theories.

Corollary (6.11) Let $M : \mathcal{T} \to \mathcal{V}$ be a functor from an essentially algebraic theory $\mathcal{T}$. Then the following are equivalent:

• $M$ is left exact, and hence an algebra.
• $M$ is a filtered colimit in $\mathcal{V}\text{-Cat}(\mathcal{T}, \mathcal{V})$ of representables.
• $M$ is an element of the filtered-colimit completion of $\mathcal{T}^{\text{op}}$ (as the completion of $\mathcal{T}^{\text{op}} \hookrightarrow \mathcal{V}\text{-Cat}(\mathcal{T}, \mathcal{V})$ under filtered colimits).

The appearance of filtered colimits in this theorem suggests that our brief aside into essentially algebraic theories is anything but an aside.

That Wasn’t an Aside!

In this section, we will see that locally finitely presentable categories and essentially algebraic theories are closely intertwined. In fact, we will show that essentially algebraic theories present l.f.p. categories, and that this gives rise to a duality between a doctrine of theories and a doctrine of l.f.p. categories. I’m using the word “doctrine” here to mean just a “theory of theories”. Thus, categories whose objects are glued together out of finite shapes are precisely the categories of algebras for essentially algebraic theories.

We begin with the following theorem.

Lemma (7.2) Let $\mathcal{C}$ be l.f.p.. Then $\mathcal{C} \simeq \text{Lex}(\mathcal{C}_f^{\text{op}}, \mathcal{V})$.

Proof By $6.11$, this is equivalent to $\mathcal{C}$ being the filtered-colimit completion of $\mathcal{C}_f^{\text{op}}$, which holds by (the rest of) $7.2$.

Since this says that $\mathcal{C}$ is the category of algebras of $\mathcal{C}_f^{\text{op}}$, we can see $\mathcal{C}_f^{\text{op}}$ as “the theory of an object of $\mathcal{C}$”. As an example, this shows that the essentially algebraic theory of groups is equivalent to the opposite of the category of finitely presentable groups. Since a finitely presentable group is a coequalizer of finitely generated free groups, left exact functors out of this category are determined by their actions on the finitely generated free groups. We ran into the fact that the opposite of the category of finitely generated free groups determines the Lawvere theory of groups before; we are seeing this fact again, but in some more generality.

Now, let’s turn out attention to the restriction and extension of scalars between theories. Let $F : \mathcal{T} \to \mathcal{T}'$ be a lex functor between theories. Since composites of lex functors are lex, we get a functor $$F^\ast : \text{Lex}(\mathcal{T}', \mathcal{V}) \to \text{Lex}(\mathcal{T}, \mathcal{V})$$ by precomposition. This is the restriction of scalars functor; between theories of modules of rings it would be just that. We call functors $F^{\ast} : \text{Alg}_{\mathcal{T}'} \to \text{Alg}_{\mathcal{T}}$ induced in this way algebraic functors.

Corollary (9.5, 6.12) $F^\ast$ is finitary, and therefore $\text{colim}_F : \mathcal{V}\text{-Cat}(\mathcal{T}, \mathcal{V}) \to \mathcal{V}\text{-Cat}(\mathcal{T}', \mathcal{V})$ (by which I mean left Kan extension along $F$) descends to $F_{\ast} : \text{Lex}(\mathcal{T}, \mathcal{V}) \to \text{Lex}(\mathcal{T}', \mathcal{V})$ which is left adjoint to $F^\ast$.

Adjoint to the restriction of scalars, we get our usual extension of scalars functor. As a corollary, we get the following nice result.

Corollary The category of algebras of a theory $\mathcal{T}$ is a reflective subcategory of the category $\mathcal{V}^{\mathcal{T}}$ of copresheaves on it.

Proof $$\text{Alg}_{\mathcal{T}} \hookrightarrow \mathcal{V}\text{-Cat}(\mathcal{T}, \mathcal{V}) \cong \text{Lex}(\mathcal{L}_{\mathcal{T}}, \mathcal{V})$$ is algebraic, given by the reflection $\mathcal{L}_{\mathcal{T}} \to \mathcal{T}$ of $\mathcal{T} \hookrightarrow \mathcal{L}_{\mathcal{T}}$ sending formal limits to the actual limits in $\mathcal{T}$.

Now, a few sections ago we proved that reflective subcategories of presheaves were locally finitely presentable. Therefore, we can turn the previous corollary into the following theorem.

Theorem (9.8) For a finitary theory $\mathcal{T}$,

• the category $\text{Alg}_{\mathcal{T}}$ of $\mathcal{T}$-algebras is l.f.p.,
• $\text{Alg}_{\mathcal{T} f}$ is the essential image of $\mathcal{T}^{\text{op}} \hookrightarrow \text{Alg}_{\mathcal{T}}$, and
• $\text{Alg}_{\mathcal{T} f} \simeq \mathcal{T}^{\text{op}}$.

This theorem intertwines l.f.p. categories and essentially algebraic theories in the following precise way.

Corollary A category $\mathcal{C}$ is l.f.p. precisely when it is the category of algebras for a finitary theory (which is then equivalent to $\mathcal{C}_f^{\text{op}}$.)

In fact, we can say something more. Since categories of algebras are l.f.p., a functor $F^{\ast} : \text{Alg}_{\mathcal{T}'} \to \text{Alg}_{\mathcal{T}}$ has a left adjoint if it is finitary and continuous. If this occurs, then its adjoint $F_{\ast}$ preserves f.p. objects by the following calculation. $$\begin{aligned} \text{Alg}_{\mathcal{T}'}(F_{\ast}X, \colim -) &\cong \text{Alg}_{\mathcal{T}}(X, F^{\ast}\colim -) &\qquad\text{by adjointness,}\\ &\cong \text{Alg}_{\mathcal{T}}(X, \colim F^{\ast} -) &\qquad\text{by finitariness,}\\ &\cong \colim \text{Alg}_{\mathcal{T}}(X, F^{\ast}-) &\qquad\text{by f.p.}\\ &\cong \colim \text{Alg}_{\mathcal{T}'}(F_{\ast}X, -) &\qquad\text{by adjointness.} \end{aligned}$$

Therefore, $F_{\ast}$ restricts to a functor $\mathcal{T}^{\text{op}} \to \mathcal{T}'^{\text{op}}$, and as a left adjoint it is cocontinuous. Therefore, $F_{\ast} : \mathcal{T} \to \mathcal{T}'$ commutes with limits. We have shown that $F^{\ast}$ is algebraic precisely when it is finitary and continuous, and we can bundle all of this up into the following general theorem.

Theorem (9.14) Let

• $\mathcal{V}\text{-Th}$ be the $\mathcal{V}\text{-Cat}$ enriched category of theories and lex functors, and
• $\mathcal{V}\text{-lfp}$ be the $\mathcal{V}\text{-Cat}$ enriched category of l.f.p. $\mathcal{V}$-categories and finitary right adjoint functors.

Then

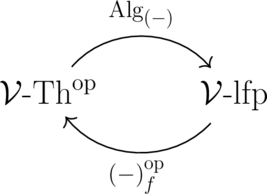
is a bi-equivalence.

Over sets, this bi-equivalence is called the Gabriel-Ulmer duality. Following Lawvere, we could call this contravariant bi-equivalence the “structure-semantics duality”. The structure map is the one which extracts the finite objects from an l.f.p. category, and the semantics map takes a theory to its category of algebras. In the language of this post, this bi-equivalence shows that categories whose objects can be glued together out of finite shapes and the suitably finite functors between them are presented by essentially algebraic theories. On this blog, David Corfield has discussed other variants of this sort of duality.

Concluding Thoughts

We’ve covered a lot of ground in this blog post, and we’ve still managed to skip out on big sections of Kelly’s paper. In particular, we missed section 5 relating finite presentability over a general base to finite presentability over sets, section 6 studying flatness of functors, section 8 concerning local finite presentability over sets in more detail, and section 10 which concerns sketches. Here are some of the things we did get to see.

• Weighted (co)limits as the enriched version of (co)limits.
• Objects being glued together out of figures of “tractable shape”.
• A definition of “finite” in the general categorical context.
• A characterization of the categories whose objects are glued together out of finite shapes.
• A general notion of “algebraic theory”, general enough to include the dual of the finite shapes.
• That the models of this theory (dual to the finite shapes) are precisely the objects of the category.