Coarse-Graining Open Markov Processes
Posted by John Baez
Kenny Courser and I have been working hard on this paper for months:
- John Baez and Kenny Courser, Coarse-graining open Markov processes.
It may be almost done. So, it would be great if you folks could take a look and comment on it! It’s a cool mix of probability theory and double categories.
‘Coarse-graining’ is a standard method of extracting a simple Markov process from a more complicated one by identifying states. We extend coarse-graining to open Markov processes. An ‘open’ Markov process is one where probability can flow in or out of certain states called ‘inputs’ and ‘outputs’. One can build up an ordinary Markov process from smaller open pieces in two basic ways:
- composition, where we identify the outputs of one open Markov process with the inputs of another,
and
- tensoring, where we set two open Markov processes side by side.
A while back, Brendan Fong, Blake Pollard and I showed that these constructions make open Markov processes into the morphisms of a symmetric monoidal category:
- A compositional framework for Markov processes, -Category Café, January 12, 2016.
Here Kenny and I go further by constructing a symmetric monoidal double category where the 2-morphisms include ways of coarse-graining open Markov processes. We also extend the previously defined ‘black-boxing’ functor from the category of open Markov processes to this double category.
But before you dive into the paper, let me explain all this stuff a bit more….
Very roughly speaking, a ‘Markov process’ is a stochastic model describing a sequence of transitions between states in which the probability of a transition depends only on the current state. But the only Markov processes talk about are continuous-time Markov processes with a finite set of states. These can be drawn as labeled graphs:
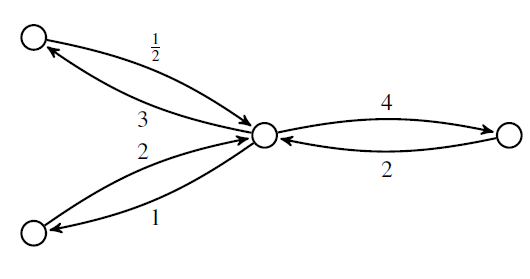
where the number labeling each edge describes the probability per time of making a transition from one state to another.
An ‘open’ Markov process is a generalization in which probability can also flow in or out of certain states designated as ‘inputs’ and outputs’:
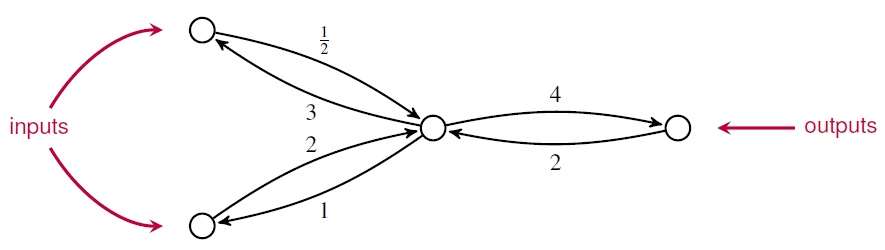
Open Markov processes can be seen as morphisms in a category, since we can compose two open Markov processes by identifying the outputs of the first with the inputs of the second. Composition lets us build a Markov process from smaller open parts — or conversely, analyze the behavior of a Markov process in terms of its parts.
In this paper, Kenny extend the study of open Markov processes to include coarse-graining. ‘Coarse-graining’ is a widely studied method of simplifying a Markov process by mapping its set of states onto some smaller set in a manner that respects the dynamics. Here we introduce coarse-graining for open Markov processes. And we show how to extend this notion to the case of maps that are not surjective, obtaining a general concept of morphism between open Markov processes.
Since open Markov processes are already morphisms in a category, it is natural to treat morphisms between them as morphisms between morphisms, or ‘2-morphisms’. We can do this using double categories!
Double categories were first introduced by Ehresmann. Since then, they’ve used in topology and other branches of pure math—but more recently they’ve been used to study open dynamical systems and open discrete-time Markov chains. So, it should not be surprising that they are also useful for open Markov processes..
As a bunch of you already know, a 2-morphism in a double category looks like this:

While a mere category has only objects and morphisms, here we have a few more types of things. We call and ‘objects’, and ‘vertical 1-morphisms’, and ‘horizontal 1-cells’, and a ‘2-morphism’. We can compose vertical 1-morphisms to get new vertical 1-morphisms and compose horizontal 1-cells to get new horizontal 1-cells. We can compose the 2-morphisms in two ways: horizontally by setting squares side by side, and vertically by setting one on top of the other.
In a ‘strict’ double category all these forms of composition are associative. In a ‘pseudo’ double category, horizontal 1-cells compose in a weakly associative manner: that is, the associative law holds only up to an invertible 2-morphism, the ‘associator’, which obeys a coherence law.
Kenny and I construct a double category with:
- finite sets as objects,
- maps between finite sets as vertical 1-morphisms,
- open Markov processes as horizontal 1-cells,
- morphisms between open Markov processes as 2-morphisms.
I won’t give the definition of item 4 here; you gotta read our paper for that! Composition of open Markov processes is only weakly associative, so is a pseudo double category.
This is how our paper goes. In Section 2 we define open Markov processes and steady state solutions of the open master equation. In Section 3 we introduce coarse-graining first for Markov processes and then open Markov processes. In Section 4 we construct the double category described above. We prove this is a symmetric monoidal double category in the sense defined by Mike Shulman. This captures the fact that we can not only compose open Markov processes but also ‘tensor’ them by setting them side by side.
For example, if we compose this open Markov process:
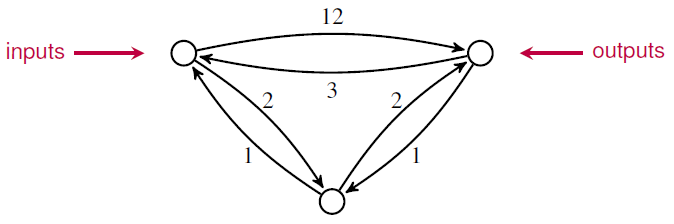
with the one I showed you before:

we get this open Markov process:
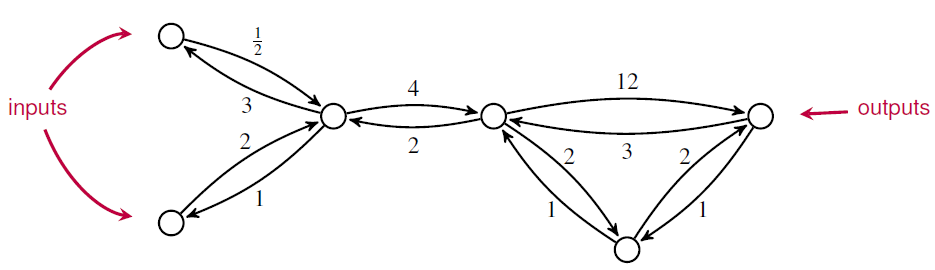
But if we tensor them, we get this:
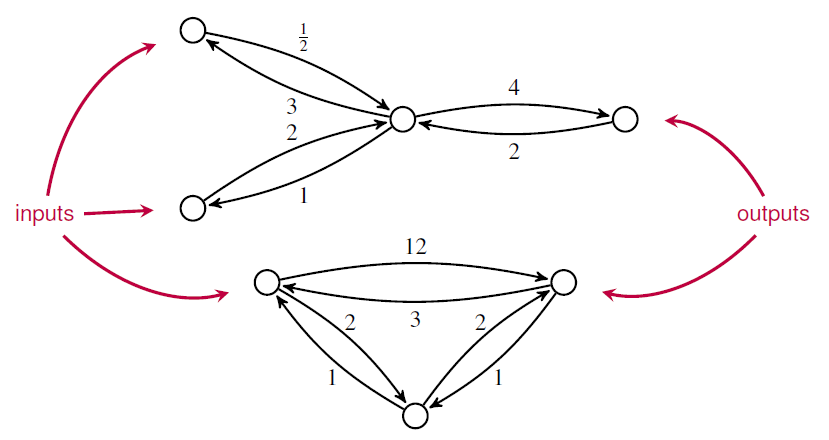
As compared with an ordinary Markov process, the key new feature of an open Markov process is that probability can flow in or out. To describe this we need a generalization of the usual master equation for Markov processes, called the ‘open master equation’.
This is something that Brendan, Blake and I came up with earlier. In this equation, the probabilities at input and output states are arbitrary specified functions of time, while the probabilities at other states obey the usual master equation. As a result, the probabilities are not necessarily normalized. We interpret this by saying probability can flow either in or out at both the input and the output states.
If we fix constant probabilities at the inputs and outputs, there typically exist solutions of the open master equation with these boundary conditions that are constant as a function of time. These are called ‘steady states’. Often these are nonequilibrium steady states, meaning that there is a nonzero net flow of probabilities at the inputs and outputs. For example, probability can flow through an open Markov process at a constant rate in a nonequilibrium steady state. It’s like a bathtub where water is flowing in from the faucet, and flowing out of the drain, but the level of the water isn’t changing.
Brendan, Blake and I studied the relation between probabilities and flows at the inputs and outputs that holds in steady state. We called the process of extracting this relation from an open Markov process ‘black-boxing’, since it gives a way to forget the internal workings of an open system and remember only its externally observable behavior. We showed that black-boxing is compatible with composition and tensoring. In other words, we showed that black-boxing is a symmetric monoidal functor.
In Section 5 of our new paper, Kenny and I show that black-boxing is compatible with morphisms between open Markov processes. To make this idea precise, we prove that black-boxing gives a map from the double category to another double category, called , which has:
- finite-dimensional real vector spaces as objects,
- linear maps as vertical 1-morphisms from to ,
- linear relations as horizontal 1-cells from to ,
- squares
obeying as 2-morphisms.
Here a ‘linear relation’ from a vector space to a vector space is a linear subspace . Linear relations can be composed in the usual way we compose relations. The double category becomes symmetric monoidal using direct sum as the tensor product, but unlike it is a strict double category: that is, composition of linear relations is associative.
Our main result, Theorem 5.5, says that black-boxing gives a symmetric monoidal double functor
As you’ll see if you check out our paper, there’s a lot of nontrivial content hidden in this short statement! The proof requires a lot of linear algebra and also a reasonable amount of category theory. For example, we needed this fact: if you’ve got a commutative cube in the category of finite sets:
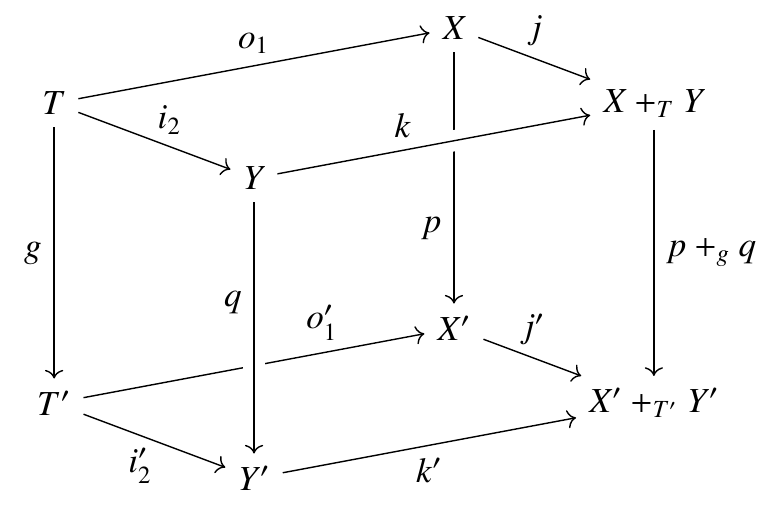
and the top and bottom faces are pushouts, and the two left-most faces are pullbacks, and the two left-most arrows on the bottom face are monic, then the two right-most faces are pullbacks. I think it’s cool that this is relevant to Markov processes!
Finally, in Section 6 we state a conjecture. First we use a technique invented by Mike Shulman to construct symmetric monoidal bicategories and from the symmetric monoidal double categories and . We conjecture that our black-boxing double functor determines a functor between these symmetric monoidal bicategories. This has got to be true. However, double categories seem to be a simpler framework for coarse-graining open Markov processes.
Finally, let me talk a bit about some related work. As I already mentioned, Brendan, Blake and I constructed a symmetric monoidal category where the morphisms are open Markov processes. However, we formalized such Markov processes in a slightly different way than Kenny and I do now. We defined a Markov process to be one of the pictures I’ve been showing you: a directed multigraph where each edge is assigned a positive number called its ‘rate constant’. In other words, we defined it to be a diagram
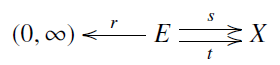
where is a finite set of vertices or ‘states’, is a finite set of edges or ‘transitions’ between states, the functions give the source and target of each edge, and gives the rate constant for each transition. We explained how from this data one can extract a matrix of real numbers called the ‘Hamiltonian’ of the Markov process, with two properties that are familiar in this game:
- if ,
- for all .
A matrix with these properties is called ‘infinitesimal stochastic’, since these conditions are equivalent to being stochastic for all .
In our new paper, Kenny and I skip the directed multigraphs and work directly with the Hamiltonians! In other words, we define a Markov process to be a finite set together with an infinitesimal stochastic matrix . This allows us to work more directly with the Hamiltonian and the all-important ‘master equation’
which describes the evolution of a time-dependent probability distribution .
Clerc, Humphrey and Panangaden have constructed a bicategory with finite sets as objects, ‘open discrete labeled Markov processes’ as morphisms, and ‘simulations’ as 2-morphisms. The use the word ‘open’ in a pretty similar way to me. But their open discrete labeled Markov processes are also equipped with a set of ‘actions’ which represent interactions between the Markov process and the environment, such as an outside entity acting on a stochastic system. A ‘simulation’ is then a function between the state spaces that map the inputs, outputs and set of actions of one open discrete labeled Markov process to the inputs, outputs and set of actions of another.
Another compositional framework for Markov processes was discussed by de Francesco Albasini, Sabadini and Walters. They constructed an algebra of ‘Markov automata’. A Markov automaton is a family of matrices with non-negative real coefficients that is indexed by elements of a binary product of sets, where one set represents a set of ‘signals on the left interface’ of the Markov automata and the other set analogously for the right interface.
So, double categories are gradually invading the theory of Markov processes… as part of the bigger trend toward applied category theory. They’re natural things; scientists should use them.

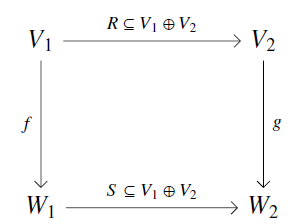
Re: Coarse-Graining Open Markov Processes
I’m getting ” /home/baez/coarse.pdf was not found on this server” when I click the link for the paper.