Re: How Much Work Can It Be To Add Some Things Up?
Here’s how I worked through this.
You didn’t write down an equation for adding three things, but I think it should have the form
That is, the function is a 2-cocycle on the monoid .
I think this already implies all the “higher” identities (i.e., all the ways for computing the work for adding numbers come out the same).
I figured you probably wanted , i.e., is a normalized 2-cocycle. Even if not, we can write , where is normalized 2-cocycle.
Let . Then is also a 2-cocycle (and is normalized). In fact, is biadditive:
and antisymmetric: . (Note that any biadditive is a 2-cocycle.)
Now, if is actually a 2-cocycle on the group , then I’m in good shape, because any such cocycle has the form
where is an anti-symmetric bilinear function and is a 2-coboundary, i.e., is some function and
I.e., group cohomology the group of alternating bilinear functions , and two 2-cocycles and represent the same cohomology class if their anti-symmetrizations coincide.
I’m not entirely sure it’s the same for , but let’s go with it for now.
If we also require that be symmetric (which I don’t think you actually specified), then clearly , so .
In which case, it comes down to having an such that . Clearly works, and presumably continuity forces this, by Alexander’s argument, giving .
I guess this remains the only answer even if we don’t require symmetry but enforce continuity, because there are no non-trivial continuous alternating 2-forms on (and therefore none such that ).
Re: How Much Work Can It Be To Add Some Things Up?
In the interests of categorification I wanted to look
at this problem with the restricted to the positive
integers. I thought it would be easy to prove something
like which we would expect from an entropy function. Then I fell into a rabbit hole…
Taking as unknown quantities the two-place functions
there is a system of linear equations generated by the 2-cocycle condition:
as well as the linearity condition
This is an infinite set of equations, but we can
truncate to the set of unknowns
for some upper bound
I also restrict to
For example, truncating at we have a linear
system which has solution the kernel of the following matrix
The columns are labelled by the unkown.
The kernel of this matrix has dimension 3.
Fixing I found there are 6 solutions:
Notice that for all of these so this is looking promising.
I did some numerics to push these calculations further.
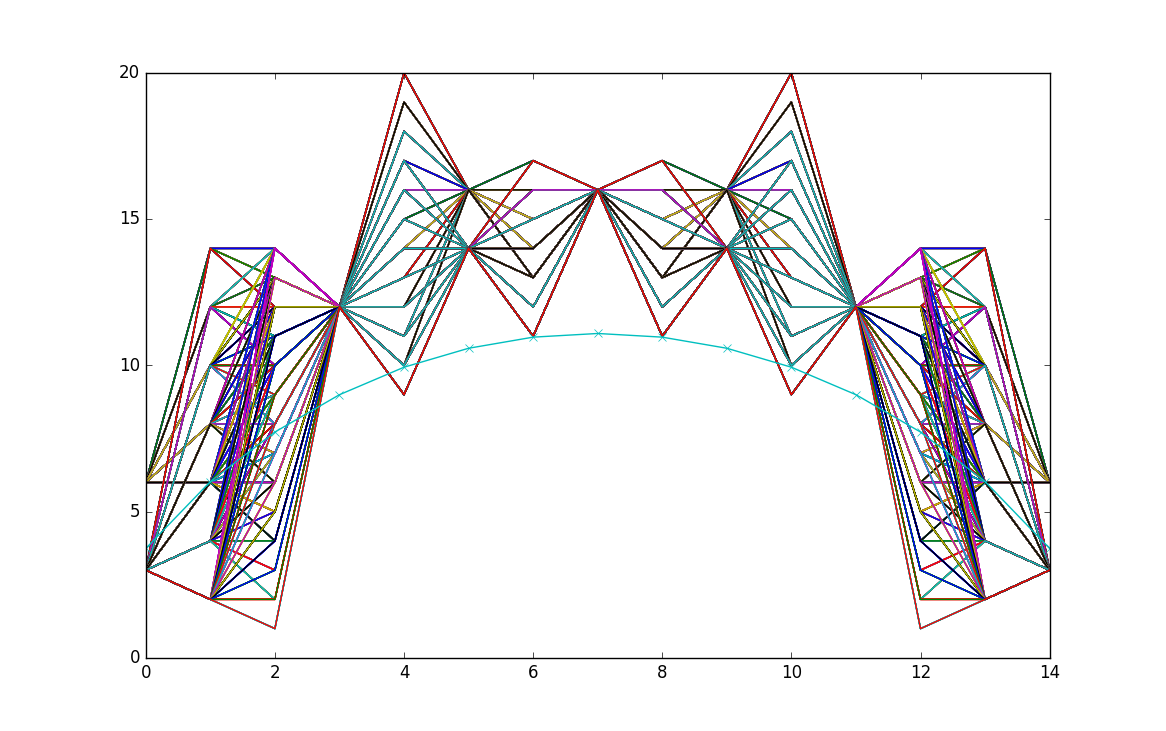
Here is a graph showing positive integer solutions
truncating at This time I fixed as there
are no solutions with
I have plotted only the values as compared to
the real solution for in cyan.
The x-axis is labelled by



Re: How Much Work Can It Be To Add Some Things Up?
Just to get the ball rolling, I’m going to pessimistically guess .