The n-Category Café

Joyal’s proof was published here:

André Joyal, Une théorie combinatoire des séries formelles. Advances in Mathematics 42 (1981), 1–82.

(I try not to link to Elsevier, as I’m permanently furious with them for draining universities of an obscene amount of our precious funds. But this is a free download. To balance my karma, let me remind you that many paywalled papers can be found on Sci-Hub for free. The most effective way to use Sci-Hub is to put the DOI of the paper you’re seeking into the search box; the text search function doesn’t seem to work very well.)

Doron Zeilberger stated Joyal’s argument concisely in one of his infamous opinions (number 108):

Going back to “beauty-bare”, nothing in set theory rivals the beauty of André Joyal’s lovely proof of Arthur Cayley’s theorem that the number of labeled trees, $T_n$, on $n$ vertices equals $n^{n-2}$. It is so beautiful that I can say it in words.

Let’s prove instead $n^2 T_n = n^n$ .

The left side counts doubly-rooted trees, which are labeled trees with a directed path (possibly of one vertex) of labeled vertices with some trees (possibly trivial one-vertex ones) hanging from them. On the other hand the right side counts the number of functions, $f$, from $\{1,\ldots,n\}$ into $\{1,\ldots,n\}$. If you draw the directed graph of such a function joining vertex $i$ to vertex $f(i)$, you would get a collection of cycles with some trees (possibly trivial one-vertex ones) hanging from them. So the left-side counts “lines of numbers” with hanging trees, and the right side counts “collection of cycles” with hanging trees. But “lines of numbers” are permutations in one-line notation, and “collection of cycles” are permutations in cycle-notation. QED!

If that’s crystal clear to you, great! You can stop reading here. But I wanted to state the argument in a more leisurely way, with pictures.

Let $X$ be a finite set. A tree on $X$ is an undirected graph with vertex-set $X$, such that there’s a unique non-backtracking path between any two vertices. Here’s a typical tree on a 22-element set $X$:

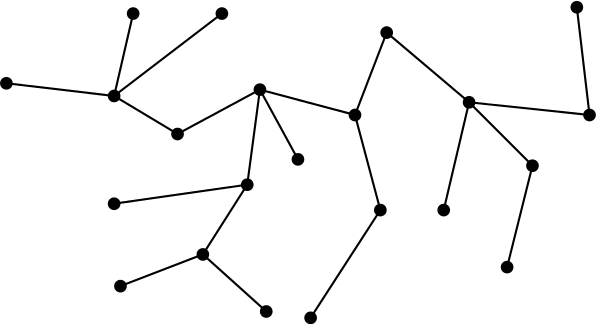
Category theorists and algebraists often use “tree” to mean rooted tree: one vertex is distinguished as special and conventionally placed at the bottom. But in the sense I’ll use the word here, trees don’t come with a distinguished vertex.

Cayley’s formula says that the number of trees on $X$ is $n^{n - 2}$, where $n$ is the cardinality of $X$. Joyal’s proof goes like this.

An equivalent statement is that the number of bipointed trees is $n^n$, where “bipointed” means that the tree comes equipped with an ordered pair of distinguished vertices (which are allowed to be the same). Here’s a bipointed tree on our 22-element set $X$, with the first distinguished vertex towards the left in brown and the second towards the right in pink (both circled):

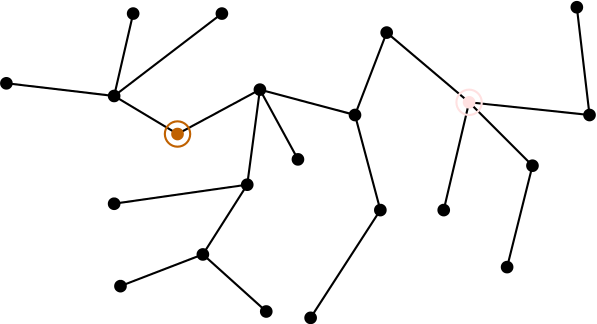
Joyal used the fabulous word vertebrate to mean bipointed tree, for reasons we’ll see in a moment. Since $n^n$ is the number of functions from $X$ to itself, Cayley’s formula says:

the number of vertebrates on $X$ is equal to the number of endofunctions of $X$.

That’s what we’ll show.

First note that by definition of tree, for any vertebrate on $X$ there’s a unique non-backtracking path from the first distinguished vertex to the second, here marked in blue:

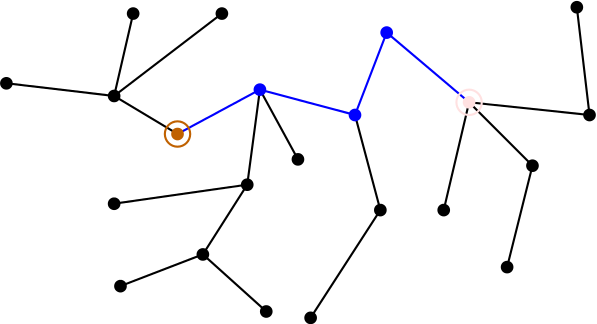
You can look at the tree as the skeleton of some fantastical creature, with the blue path as the backbone, and the vertices on it as vertebrae, with the first (brown) distinguished vertex at the head end and the second (pink) one at the tail end. Hanging off each vertebra is a rooted tree, the root being that vertebra. If you let your imagination roam free, you can picture each tree as a rather ornate limb. The most similar real-life creature I could come up with is the amazing leafy seadragon (whose existence I think I learned of from David Roberts):

Anyway, the blue path from the first distinguished vertex to the second determines a total order on the set of vertebrae. Once you’ve got that order, you might as well erase the edges between them, as they’re determined by the order. So a vertebrate amounts to a diagram like this:

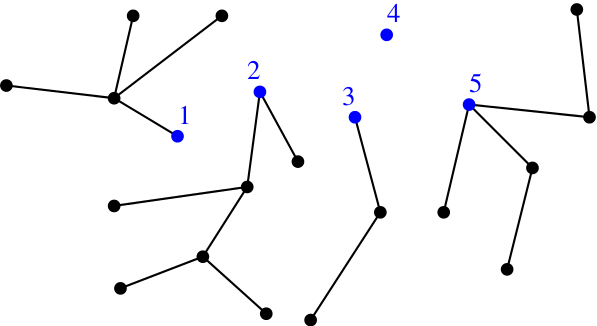
So far everything has been canonical: no arbitrary choices. The set of vertebrates on $X$ is in canonical one-to-one correspondence with diagrams of this type. But now we’re going to break that pattern, using an elementary observation:

the number of total orders on a finite set $S$ is equal to the number of permutations of $S$.

Of course, both are $(\# S)!$. There’s no canonical bijection between orders on and permutations of an abstract set $S$ — for if there were, which order would correspond to the identity permutation? But that’s OK: all we need here is that there’s some bijection.

So, let’s arbitrarily choose, for each $S \subseteq X$, a bijection between orders on $S$ and permutations of $S$. This done, we can replace the ordering of our five-element subset with a permutation of it. Which particular permutation it is depends on that arbitrary choice of bijection, but let’s say for sake of argument that it’s this one:

Hanging off each vertebra (yellow vertex) is a rooted tree. It makes no difference if we adorn its edges with arrows directed towards the root:

(There’s no choice involved in doing this.) Now what we’ve got is a directed graph with $X$ as its vertex-set, and with the property that each vertex is the source (tail) of exactly one arrow. This is nothing but a function $f: X \to X$! We seem to have also chosen a distinguished set of vertices, the yellow ones. But actually, they’re determined by $f$: they’re exactly the periodic points. So we lose no information if we throw away the colouring:

So what we have is precisely an endofunction of $X$.

We’ve now shown that the vertebrates (bipointed trees) on $X$ are in bijection with the endofunctions of $X$. Since there are $n^n$ such functions, where $n = \# X$, it follows that there are $n^n$ vertebrates on $X$, and therefore $n^{n - 2}$ unrooted trees on $X$. And that’s Joyal’s proof of Cayley’s theorem.

Of course, the argument I’ve given is pictorial and not entirely rigorous. I didn’t even define “tree” rigorously. Probably the best way to make it rigorous is via species, the concept that Joyal pioneered in that same paper.

I’m not going to give a full introduction to species here, but let me just say briefly how it works. A species is a functor from the category of finite sets and bijections to the category of sets. For example, there’s a species $Ord$ that assigns to each finite set the set of total orders on it. There are several ways of putting two species together to make a third, and in particular, species can be “composed”. We’ve essentially shown that

$$Tree_{\ast\ast} \cong Ord \circ Tree_{\ast},$$

where $Tree_{\ast\ast}$ is the species of vertebrates (bipointed trees), $Tree_{\ast}$ is the species of rooted (pointed) trees, and $\circ$ is composition. This isomorphism expresses the fact explained in the first few pictures above: that a vertebrate is the same thing as a collection of rooted trees, with a total order on them (1–5 in the example shown). On the other hand, we also have

$$End \cong Perm \circ Tree_{\ast},$$

where $End$ is the species of endofunctions and $Perm$ is the species of permutations. This isomorphism expresses the fact explained in the last few pictures above: that an endofunction is the same thing as a collection of rooted trees, with a permutation of them.

Now $Ord$ and $Perm$ are not isomorphic species; that is, as functors they are not naturally isomorphic. So we’re not going to conclude that $Tree_{\ast\ast}$ and $End$ are isomorphic species either. However, $Ord$ and $Perm$ are pointwise isomorphic, in the sense that $Ord(X)$ and $Perm(X)$ have the same number of elements for each finite set $X$ (namely, $(\# X)!$). It follows that $Tree_{\ast\ast}$ and $End$ are pointwise isomorphic too. In other words: on any finite set, there are the same number of vertebrates and endofunctions. That’s Cayley’s theorem.