Random Permutations (Part 7)
Posted by John Baez
Last time I computed the expected number of cycles of length in a random permutation of an -element set. The answer is wonderfully simple: for all .
As Mark Meckes pointed out, this fact is just a shadow of a more wonderful fact. Let be the number of cycles of length in a random permutation of an -element set, thought of as a random variable. Then as , the distribution of approaches a Poisson distribution with mean .
But this is just a shadow of an even more wonderful fact!
First, if we fix some number , and look at all the random variables , they converge to independent Poisson distributions as .
In fact we can even let as , so long as outstrips , in the following sense: . The random variables will still converge to independent Poisson distributions.
These facts are made precise and proved here:
- Richard Arratia and Simon Tavaré, The cycle structure of random permutations, The Annals of Probability 20 (1992), 1567–1591.
In the proof they drop another little bombshell. Suppose . Then the random variables and become uncorrelated as soon as gets big enough for a permutation of an -element set to have both a -cycle and a -cycle. That is, their expected values obey
whenever . Of course when it’s impossible to have both a cycle of length and one of length , so in that case we have
It’s exciting to me how the expected value pops suddenly from to as soon as our set gets big enough to allow both a -cycle and a -cycle. It says that in some sense the presence of a large cycle in a random permutation does not discourage the existence of other large cycles… unless it absolutely forbids it!
This is a higher-level version of a phenomenon we’ve already seen: jumps from to as soon as .
More generally, Arratia and Tavaré show that
whenever . But on the other hand, clearly
whenever , at least if the numbers are distinct. After all, it’s impossible for a permutation of a finite set to have cycles of different lengths that sum to more than the size of that set.
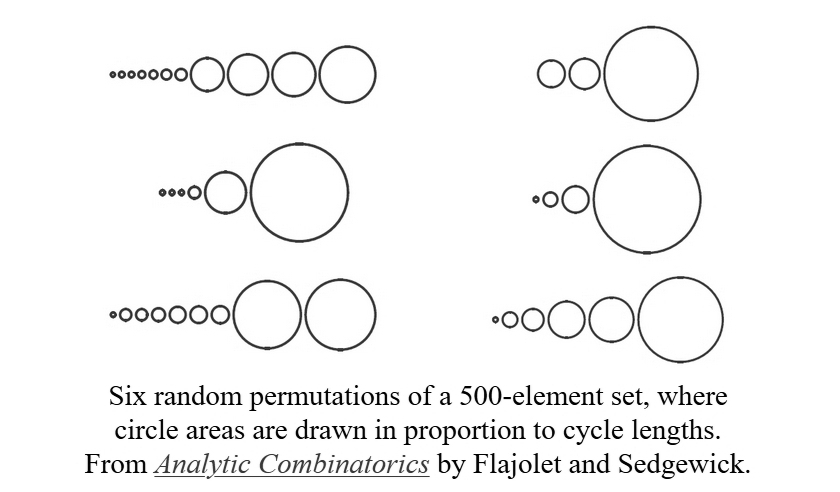
I’m trying to understand the nature of random permutations. These results help a lot. But instead of describing how they’re proved, I want to conclude with a picture that has also helped me a lot:
One can argue that Flajolet and Sedgewick should have used circumferences rather than areas to indicate cycle lengths: after all, the circumference is a kind of ‘cycle length’. That would have made the large cycles seem even larger compared to the puny ones.
Of course, experts on the visual display of quantitative information have a lot of opinions on these issues. But never mind! Let’s extract some morals from this chart.
We can see that a random permutation of a large set has rather few cycles on average. To be precise, the expected number of cycles in a random permutation of an -element set is .
We can also see that the lengths of the cycles range dramatically from tiny to large. To be precise, suppose . Then since the expected number of cycles of length is , the expected number of cycles of length between and is close to
Thus we can expect as many cycles of length between and as between and , or between and , etc.
So, I’m now imagining a random permutation of a large set as a way of chopping up a mountain into rocks with a wild range of sizes: some sand grains, some pebbles, some fist-sized rocks and some enormous boulders. Moreover, as long as two different sizes don’t add up to more than the size of our mountain, the number of rocks of those two sizes are uncorrelated.
I want to keep improving this intuition. For example, if and , are the random variables and independent, or just uncorrelated?

Re: Random Permutations (Part 7)
Maybe some of you can help me understand (and thereby prove) Equations 5 and 6 in Arratia and Tavare’s paper. They cite another paper for this equation, from a journal on population biology! But I think it should be easy and fun to figure out ourselves.
These equations concern the random variable that I was discussing: the number of cycles of length in a random permutation of an -element set. It’s a formula for expected values of products of such random variables.
We take a list of numbers and compute the expected value of the random variable
where the underline indicates ‘falling powers’:
Equation 5 says that
or in other words
if . It also says that if this inequality is violated, the expected value is . So, the main thing I need to understand is this equation.
But then, in Equation 6, they reformulate this equation very suggestively as follows, given that the inequality holds:
where the are independent Poisson distributions with means . To see why this reformulation works, I just need to see why
This must be a famous thing about Poisson distributions. I think I’ve even used it before in my own work. I bet one proof uses Dobiński’s formula for the number of partitions of an -element set. If we go this route, I’ll probably need to use the relation between partitions and permutations to figure out what’s really going on here.