Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

January 23, 2023

Question on Condensed Matter Physics

Posted by John Baez

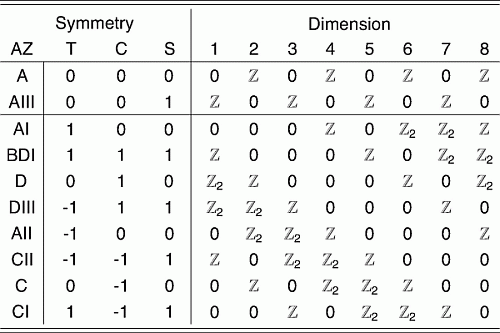
The tenfold way is a mathematical classification of Hamiltonians used in condensed matter physics, based on their symmetries. Nine kinds are characterized by choosing one of these 3 options:

  • antiunitary time-reversal symmetry with T 2=1T^2 = 1, with T 2=−1T^2 = -1, or no such symmetry.

and one of these 3 options:

  • antiunitary charge conjugation symmetry with C 2=1C^2 = 1, with C 2=−1C^2 = -1, or no such symmetry.

(Charge conjugation symmetry in condensed matter physics is usually a symmetry between particles - e.g. electrons or quasiparticles of some sort - and holes.)

The tenth kind has unitary “SS” symmetry, a symmetry that simultaneously reverses the direction of time and interchanges particles and holes. Since it is unitary and we’re free to multiply it by a phase, we can assume without loss of generality that S 2=1S^2 = 1.

What are examples of real-world condensed matter systems of all ten kinds?

I’ll take what I can get! If you know materials of a few of the ten kinds, that’s a start!

Posted at January 23, 2023 7:43 PM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/3446



9 Comments & 0 Trackbacks

p-n junctions

I think p-n junctions would be the tenth type. Not confident though. https://en.wikipedia.org/wiki/P%E2%80%93n_junction

Posted by: Steve Huntsman on January 24, 2023 1:32 PM | Permalink | Reply to this

Re: p-n junctions

This is a good example to think about. If I had to guess, I’d guess this system has both TT and CC symmetry separately, not just the combined symmetry where we switch electrons and holes and reverse the direction of time. And since electrons are spin-1/2 particles I’d guess T 2=−1T^2 = -1: that’s how it usually goes, since the antiunitaries that commute with the SU(2)SU(2) action on ℂ 2\mathbb{C}^2 all square to −1-1. I can’t even guess about C 2C^2. But surely someone must know!

Posted by: John Baez on January 27, 2023 1:29 AM | Permalink | Reply to this

Re: Question on Condensed Matter Physics

See table II of

for a list of realizations, as of 2010, in either experimental systems or in realistic models, of different symmetry classes in physical systems in 1,2, or 3 spatial dimensions. Only nontrivial realizations are given, no realization is given if the given symmetry class is trivial in the given dimension.

Posted by: matt on January 30, 2023 8:52 PM | Permalink | Reply to this

Re: Question on Condensed Matter Physics

Great, thanks! I’ve been desperate for some information like this.

Let me go through a few examples. The ten kinds of types of systems are listed here, using the Altland–Zinbauer classification:

Systems of type “BDI” have charge conjugation (CC) and time reversal (TT) symmetry with C 2=T 2=1C^2 = T^2 = 1. The paper above writes:

An example of the BDI class is a graphene ribbon, or equivalently a carbon nanotube with a zigzag edge.

This is in d=1d = 1, i.e. effectively one-dimensional space.

Posted by: John Baez on January 31, 2023 1:28 AM | Permalink | Reply to this

Re: Question on Condensed Matter Physics

I don’t know why the paper says

In this notation, systems with no symmetry are in class D

since I think systems of type D have CC symmetry with C 2=1C^2 = 1 but no TT symmetry. Systems with no symmetry should be of type A. Anyway, the paper says:

In one dimension, generic superconductors (class D) are classified by ℤ/2\mathbb{Z}/2, of which the nontrivial example is a p-wave superconductor with a single Majorana zero mode on the edge.

Posted by: John Baez on January 31, 2023 1:37 AM | Permalink | Reply to this

Re: Question on Condensed Matter Physics

Different meanings of “symmetry”. The Altland-Zirnbauer classification says that no symmetry is A because they consider the Hamiltonian to be an arbitrary Hermitian matrix, possibly with extra symmetries imposed. They are writing the Hamiltonian in terms of creation and annihilation operators. Going to class D in this case imposes some symmetries, for example relating the particle block of the matrix to the hole block. On the other hand, in the Kitaev way of discussing this, the most general case is an arbitrary Hermitian antisymmetric Hamiltonian, as the Hamiltonian is written in terms of Majorana operators. Then, “no symmetry” means that there are no operators that anticommute with this matrix, and this is class D. The Freedman et al paper uses the Kitaev notion of symmetries and for that notion “no symmetry” indeed is D.

Posted by: matt on February 2, 2023 11:36 PM | Permalink | Reply to this

Re: Question on Condensed Matter Physics

I believe that the SSH model is a 1D example in the AIII symmetry class. It is used to model trans-polyacetylene. Ryu Schnyder Furusaki and Ludwig discuss polyacetylene in section 2.2.4 of their tenfold way paper. I am not sure about experimental realization, though.

Posted by: Cameron Krulewski on February 2, 2023 9:02 PM | Permalink | Reply to this

Re: Question on Condensed Matter Physics

Thanks very much! Just for my own benefit, the AIII class is the one without CC or TT symmetry separately, just the combined SS symmetry that reverses the direction of time while interchanging particles and holes.

Posted by: John Baez on February 3, 2023 1:48 AM | Permalink | Reply to this

Re: Question on Condensed Matter Physics

This paper:

says

We see that the chiral SSH model belongs to class AIII if it lacks time-reversal and particle hole symmetries but it is in class BDI if it satisfies these symmetries and T 2=1T^2 = 1. The example we considered was in class BDI. To see this recall that our electrons were spinless.

That makes it sound like the more realistic model with spin-1/2 electrons is indeed in class AIII.

Posted by: John Baez on February 3, 2023 10:12 PM | Permalink | Reply to this

Post a New Comment