A Notion of ‘Location’ for Processes in Monoidal Categories
Posted by Emily Riehl
guest post by Ariel Rosenfield and Ariadne Si Suo
One can view a monoidal category as a collection of resources (objects) and processes for transforming resources (morphisms). A central idempotent in a monoidal category is a way to speak about the “location” of a process taking place in , but without referring to points, space, or distance. Under mild conditions on , its set of central idempotents can be viewed as a sort of “topological space internal to ,” which lets us use some tools and intuition from topology while working in .
Our Adjoint School group spent a lot of time the past few months with this paper by Rui Barbosa and Chris Heunen, which outlines a particularly cool application of this idea, namely the representation of “nice enough” monoidal categories (those satisfying the aforementioned mild conditions) as the global sections of certain sheaves. In this post, we’ll take a close look at central idempotents and two related notions, namely the restriction and support of morphisms in .
Preliminaries
People are always asking, “how can we use tools from topology in categories other than the category of spaces?” Since a topology on a space is usually defined in terms of sets of points, we might, toward answering this question, try to look for some pattern of relationships underlying a topology which we can describe without talking about points, which leads to the idea of a frame. Recall that the categories of frames, locales, and complete Heyting algebras all have the same objects, namely partially ordered sets having arbitrary joins and finite meets , and satisfying
for all and all (maybe infinite) families . This should look familiar - if is a topological space and we consider the topology on as a partially ordered set where
joins are set unions, and meets are set intersections, the first two conditions above are exactly the conditions for to constitute a topology - the third is automatically satisfied in the case where and are sets. Thus it makes sense to say that a frame is a type of lattice that captures the behavior of the open sets of a space. The category of locales is opposite to the category of frames, and so we might similarly view a locale as a type of lattice that captures the behavior of the closed sets of a space. Because our definition above makes no mention of elements of , we can find frames (or locales, if you prefer) in categories where we can’t easily speak of “elements of objects,” or speak of them at all.
Central idempotents in monoidal categories
If all that’s the case, and a frame is just the disembodied system of relationships between the open sets of a space, which we’re viewing now as dots in some category, what should serve as our new notion of open set? What should the nameless dots be?
Central idempotents are one answer! A good analogy to keep in mind for the rest of this discussion is “central idempotent open set of a topological space,” and we’ll see an example soon that justifies this analogy more rigorously. They are defined as follows: A central idempotent in a small monoidal category with left unitor and right unitor is a morphism satisfying
(Idempotency 1) ;
(Idempotency 2) the above morphism is invertible;
(Centrality) the object U carries a half-braiding satisfying:
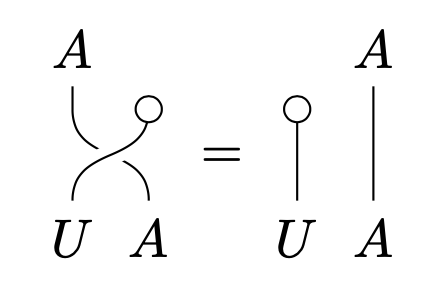
Okay, so that’s cool, but how should you think about these conditions? If you squint a little, you can see that is kind of the “intersection” of two objects of - this makes sense from the perspective on as a collection of resources, where we think of as “all instances of ( and ).” What we’re asking for with the idempotency conditions is thus something like “ for an open .”
Still squinting a little, you can think of the centrality condition as asking for something like “ for opens and .” We’ll skip the definition of a half-braiding - all of the example categories we’ll see are braided, and it’s a fact that braidings coincide with half-braidings when they’re present, so for now, we don’t need to worry about the centrality condition being satisfied.
Examples
Let’s see what central idempotents look like in some familiar categories:
Central idempotents in sheaf categories
Our motivating example is the category of sheaves on a space , whose central idempotents are exactly the open sets of . To see this, we first note that is a cartesian category whose monoidal unit is the sheaf which sends every object of the locale to the single-element set. It turns out that in any cartesian category, an object is the domain of a central idempotent if and only if it is a subobject of the monoidal unit. We know moreover that any locale is isomorphic to the locale of subsheaves of the terminal sheaf, so in particular, is isomorphic as a locale to - but this is just the locale . For purposes of a future example, we’ll note here that open subsets are represented as subsheaves of by sheaves of the form
Central idempotents in module categories
For another example, say is a commutative ring with unity , and consider the monoidal category . To characterize central idempotents in , we want to characterize all morphisms from -modules satisfying the idempotency and centrality conditions in our definition above. Since is braided monoidal, centrality is automatically satisfied. To check the idempotency conditions, recall that the left- and right- unitors in are respectively
so the given equality holds for exactly when
for every . Recall also that isomorphisms in the category of -modules are bijective module homomorphisms, so it’s enough to check that (2.2) is a bijection; i.e. that for every , there exist (say for ) such that
and that whenever , we have .
It turns out that central idempotents in correspond to idempotent ideals of : First, note that (2.3) implies that for a central idempotent in , is always an idempotent ideal of (to see this, use the homomorphism property of !). Conversely, if is an idempotent ideal, the inclusion is a central idempotent as defined above.
If you’re an algebraist, you might be wondering if there’s some connection between central idempotent elements in a ring and the categorical notion. When is assumed to be sufficiently nice, we can say that idempotent elements of correspond to central idempotents: For example, if is Noetherian, a consequence of Nakayama’s lemma from commutative ring theory is that any idempotent ideal has the form for some idempotent element . As above, the inclusion of any such ideal into is a central idempotent in .
Restriction and support of morphisms
With the analogy “central idempotent open set” in mind, we’d hope that whenever a morphism in our category is “defined” on a central idempotent , we can somehow restrict it to , in a similar sense to how a sheaf on a space yields a sheaf on any open set , viewed as a subspace. In a general monoidal category, we say that a morphism restricts to a central idempotent when it factors through , as in the commuting diagram
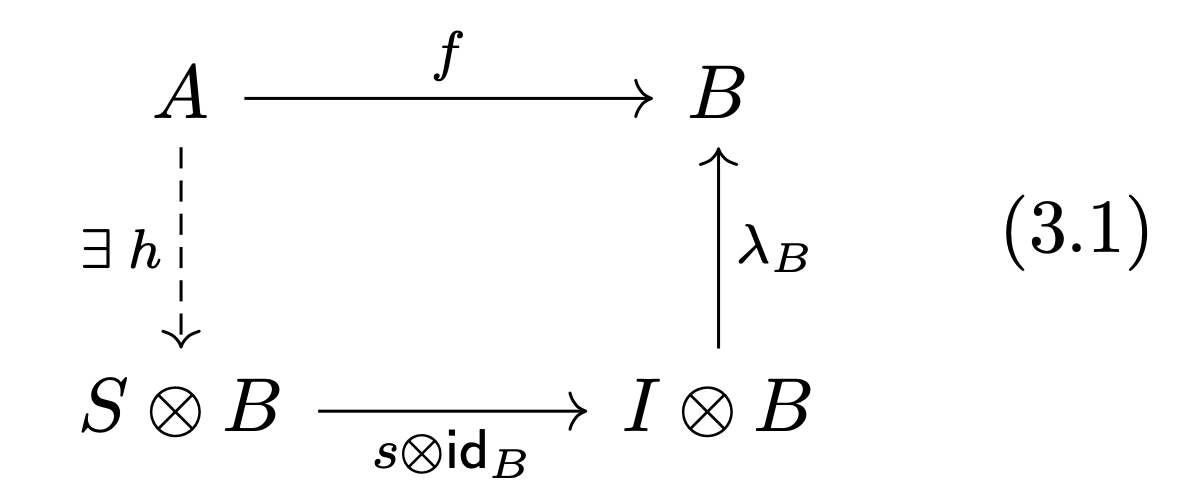
We’d also hope to be able to find the “smallest” central idempotent to which a morphism restricts, and for that we need to talk about support! Recall that the support of a function on a manifold taking values in a vector space is the closed set
where . We often regard this object as the “smallest” closed subset of containing .
Notice that being able to call a closed subset of our topological space requires that the intersection of an arbitrary family of closed sets is itself closed - a property indeed possessed by the locale of closed sets of a topological space! We can realize this notion in the generality of a monoidal category for which is a frame using central idempotents: For a morphism in , define
In this setting, the correct analogue of “a closed set containing ” is a certain morphism called a support datum. We’ll skip the precise definition, but note that for our new definition of support to capture the property of being the “smallest” closed set, we’d want to be universal amongst all support data, and it turns out that it is - any support datum factors through uniquely.
Returning to our example of , and considering an open set , observe that a morphism of sheaves satisfies the diagram (3.1) exactly when there is a natural transformation
where is the sheaf defined in (2.1), which makes (3.1) commute. Such an exists exactly when
If this condition holds, define the -component of by
No such exists if for some , since then , and there can be no map of sets . We see that the support of is just
Lattice-theoretic properties of ; sheaf representation theorems
If central idempotents are supposed to be like open sets, do they satisfy the same system of relationships satisfied by the open sets of a topological space? In other words, do they constitute the elements of a frame? The answer here is “only sometimes.”
We write for the set of central idempotents of , recalling that we take to be small. We identify central idempotents and when for an isomorphism that respects the half-braiding.
can be given the structure of a lattice. For central idempotents and in a monoidal category , we say if for a necessarily unique that respects the half-braiding. This condition is equivalent to either of the following: - is invertible. - is invertible.
Under mild conditions on , has nice lattice-theoretic properties. We’ll now define these conditions on , starting from the weakest one.
A monoidal category is stiff if
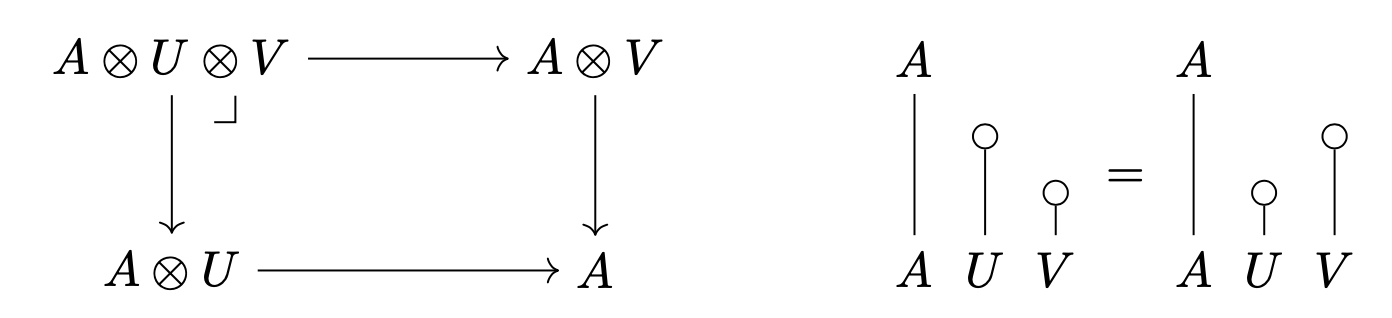
is a pullback for all objects and central idempotents and . Roughly, this says that pullbacks and monoidal products are two ways to take “intersections” of central idempotents, and that they coincide. Stiffness is a very weak condition - almost every monoidal category is stiff (except probably artificially constructed counterexamples)!
A monoidal category has finite universal joins / -joins of central idempotents if - it has an initial object satisfying for all objects - has binary joins such that
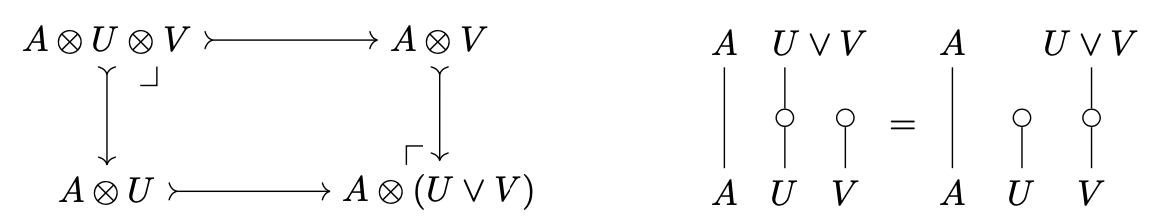
is both a pullback and pushout for all objects and central idempotents and .
This roughly says that the functor preserves joins. If has finite universal joins of central idempotents, then is a distributive lattice with least element .
A monoidal category has universal joins / -joins of central idempotents when has all joins such that the cocone
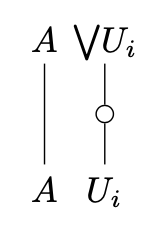
is a colimit of the diagram with morphisms
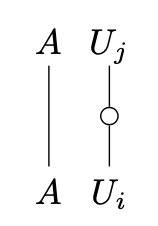
if for any set of central idempotents satisfying . This roughly says that the functor preserves suprema. If has universal joins of central idempotents, then is a frame.
It turns out that any stiff monoidal category can be freely completed with universal (finite) joins of central idempotents.
We just need a few more definitions before stating two of our aformentioned representation theorems. We say a partially ordered set is -local if implies or . A monoidal category is -local if is -local.
We say a partially ordered set is -local if implies that there exists an with . A monoidal category is -local if is -local.
As promised, here are the representation theorems:
Theorem. Any small monoidal category with universal -joins of central idempotents is monoidally equivalent to the category of global sections of a sheaf of -local monoidal categories.
Theorem. Any small monoidal category in which forms a spatial frame is monoidally equivalent to the category of global sections of a sheaf of -local monoidal categories.
Future work
In a way, a morphism restricts to a central idempotent says that “only lives over”. We can think of the support of a morphism as telling us precisely where the morphism lives.
We can extend this intuition to say that an object only lives over a central idempotent if restricts to . This is in fact equivalent to . We can define the support of an object as the support of , which tells us the precise location of .
This gives us a notion of space in a monoidal category. If we think of morphisms in a category as processes, and compositon of morphisms as processes happening one after another, then the monoidal product captures the idea of “processes happening simultaneously.” This is the natural notion of time in a monoidal category.
It seems that monoidal categories provide the perfect setting for concurrency. A classic example is the producer-consumer problem. The producer has a process of making cookies, and the consumer has a process of eating cookies. The consumer can be eating the last batch while the producer is making new ones.
Monoidal categories are perfect for modelling concurrent processes because of their natural notion of simultaneity. With the help of central idempotents and supports, we can now also talk about the space in which the processes take place. What if the producer is making cookies at the bakery, and the consumer is attending the ACT (i.e. processes have different supports)?
This motivated our research problem: What structure can we add to a monoidal category so that concurrent processes supported on disjoint central idempotents can exchange resources?

Re: A Notion of ‘Location’ for Processes in Monoidal Categories
Hmm! By coincidence I just needed this and blogged about it here last week. It’s Lemma 17: I used it to show that if is an finite-dimensional algebra over a field where the short exact sequence
splits as a sequence of -bimodules, then the ideal has the form for some idempotent . This would also work when is a Noetherian commutative ring. (I guess you’re assuming is commutative.)
I’m too scared to try to connect why I cared about this with why you care about it, but they could be related.