The n-Category Café

Two important glitches that afflict tuning systems are the Pythagorean comma and the syntonic comma. If you go up 12 fifths, multiplying the frequency by 3/2 each time, you go up a bit less than 7 octaves. The ratio is the Pythagorean comma:

$$p = 531441/524288 \approx 1.013643$$

And if you go up four fifths, you go up a bit more than 2 octaves and a major third (which ideally has a frequency ratio of 5/4). The ratio is the syntonic comma:

$$\sigma = 81/80 = 1.0125$$

In music it would be very convenient if these two glitches were the same — and sometimes musicians pretend they are. But they’re not! So their ratio shows up as a tiny meta-glitch. It’s called the ‘schisma’:

$$\chi = p/\sigma = 32805/32768 \approx 1.0011298906$$

and it was discovered by an advisor to the Gothic king Theodoric the Great — a guy named Boethius, who was later tortured and executed, presumably for unrelated reasons.

In the most widely used tuning system today, called equal temperament, a fifth is not 3/2 but slightly less: it’s

$$2^{7/12} \approx 1.498307$$

The ratio of 3/2 and this slightly smaller fifth is called the ‘grad’:

$$\gamma = p^{1/12} \approx 1.0011291504$$

Look! The grad is amazingly close to the schisma! They agree to 7 decimal places! Their ratio is a meta-meta-glitch called the Kirnberger kernel:

$$\chi/\gamma \approx 1.0000007394$$

If you unravel the mathematical coincidence that makes this happens, you’ll see it boils down to

$$2^{1/12}\, 5^{1/7} \approx 1.333333192495$$

being very close to 4/3. And this coincidence let Bach’s student Johann Kirnberger invent an amazing tuning system called rational equal temperament. It’s very close to equal temperament, but all the frequency ratios are rational.

To get this tuning system, instead of letting the fifths equal $2^{7/12}$, which is 3/2 divided by the grad, which is irrational, we try to use 3/2 divided by the schisma, which is rational. But this creates a tiny error! We deal with this by taking one of our fifths and further dividing it by the 12th power of the Kirnberger kernel — a rational number called the atom of Kirnberger:

$$\alpha = (\chi/\gamma)^{12} = 2^{161} \cdot 3^{-84} \cdot 5^{-12} \approx 1.0000088728601397$$

Rational equal temperament looks like this, with fifths labeled by their frequency ratios:

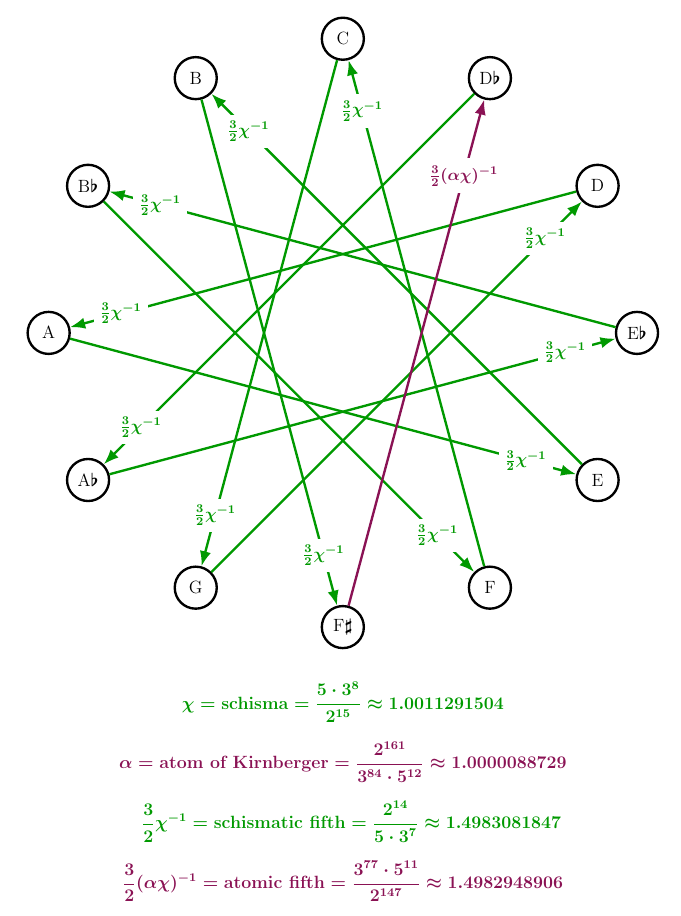
11 of the fifths are ‘schismatic fifths’ with a frequency ratio of $\frac{3}{2}\chi^{-1}$, but one is an ‘atomic fifth’ with a microscopically smaller frequency ratio, $\frac{3}{2}(\alpha \chi)^{-1}$. Both these numbers are rational, and going up 11 schismatic fifths and one atomic fifth is exactly the same as going up 7 octaves.

For comparison, here is equal temperament:

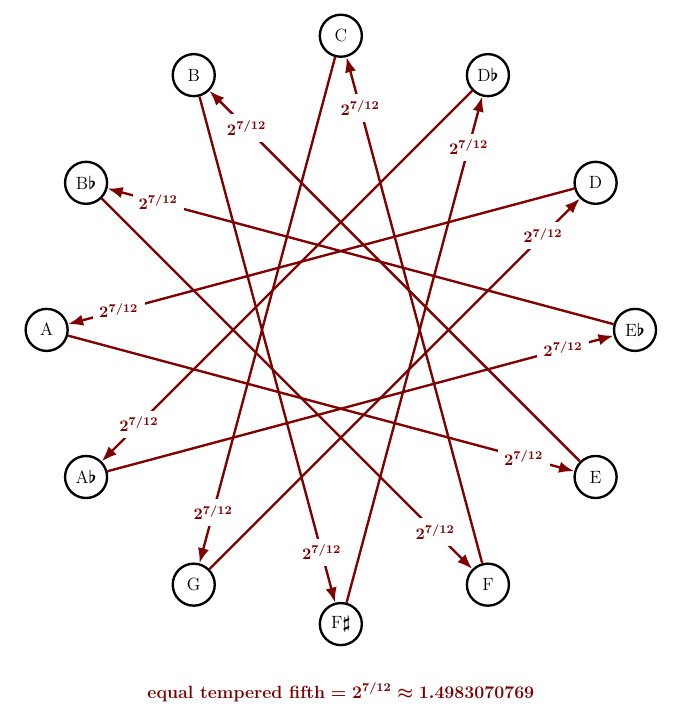
Nobody can hear the difference between rational equal temperament and equal temperament, so Kirnberger’s discovery is of purely theoretical interest. But it’s quite amazing nonetheless.

Much later the physicist Don Page, famous for discovering the ‘Page time’ in black hole physics, became so obsessed with the mathematical coincidence underlying these ideas that he wrote a paper trying to wrestle it down to something where he could do the computations in his head:

• Don N. Page, Why is the Kirnberger kernel so small?

For more details on the music theory see:

• John Baez, Well temperaments (part 3).

which is part of a long series I’m writing on the math and history of tuning systems.