Second Quantization and the Kepler Problem
Posted by John Baez
The poet Blake wrote that you can see a world in a grain of sand. But even better, you can see a universe in an atom!
Bound states of hydrogen atom correspond to states of a massless quantum particle moving at the speed of light around the Einstein universe — a closed, static universe where space is a 3-sphere. We need to use a spin-½ particle to account for the spin of the electron. The states of the massless spin-½ particle where it forms a standing wave then correspond to the orbitals of the hydrogen atom. This explains the secret 4-dimensional rotation symmetry of the hydrogen atom.
In fact, you can develop this idea to the point of getting the periodic table of elements from a quantum field theory on the Einstein universe! I worked that out here:
but you can see a more gentle explanation in the following series of blog articles.
Part 1: a quick overview of Kepler’s work on atoms and the solar system, and more modern developments.
Part 2: why the eccentricity vector is conserved for a particle in an inverse square force, and what it means.
Part 3: why the momentum of a particle in an inverse square force moves around in a circle.
Part 4: why the 4d rotation group acts on bound states of a particle in an attractive inverse square force.
Part 5: quantizing the bound states of a particle in an attractive inverse square force, and getting the Hilbert space for bound states of a hydrogen atom, neglecting the electron’s spin.
Part 6: how the Duflo isomorphism explains quantum corrections to the hydrogen atom Hamiltonian.
Part 7: why the Hilbert space of bound states for a hydrogen atom including the electron’s spin is
Part 8: why is also the Hilbert space for a massless spin-1/2 particle in the Einstein universe.
Part 9: a quaternionic description of the hydrogen atom’s bound states (a digression not needed for later parts).
Part 10: changing the complex structure on to eliminate negative-energy states of the massless spin-1/2 particle, as often done.
Part 11: second quantizing the massless spin-1/2 particle and getting a quantum field theory on the Einstein universe, or alternatively a theory of collections of electrons orbiting a nucleus.
Part 12: obtaining the periodic table of elements from a quantum field theory on the Einstein universe.
I explain how the Hamiltonian of this quantum field theory has to be tweaked a bit to give the ‘Madelung rules’ for the order in which electrons get added as we go along the periodic table:

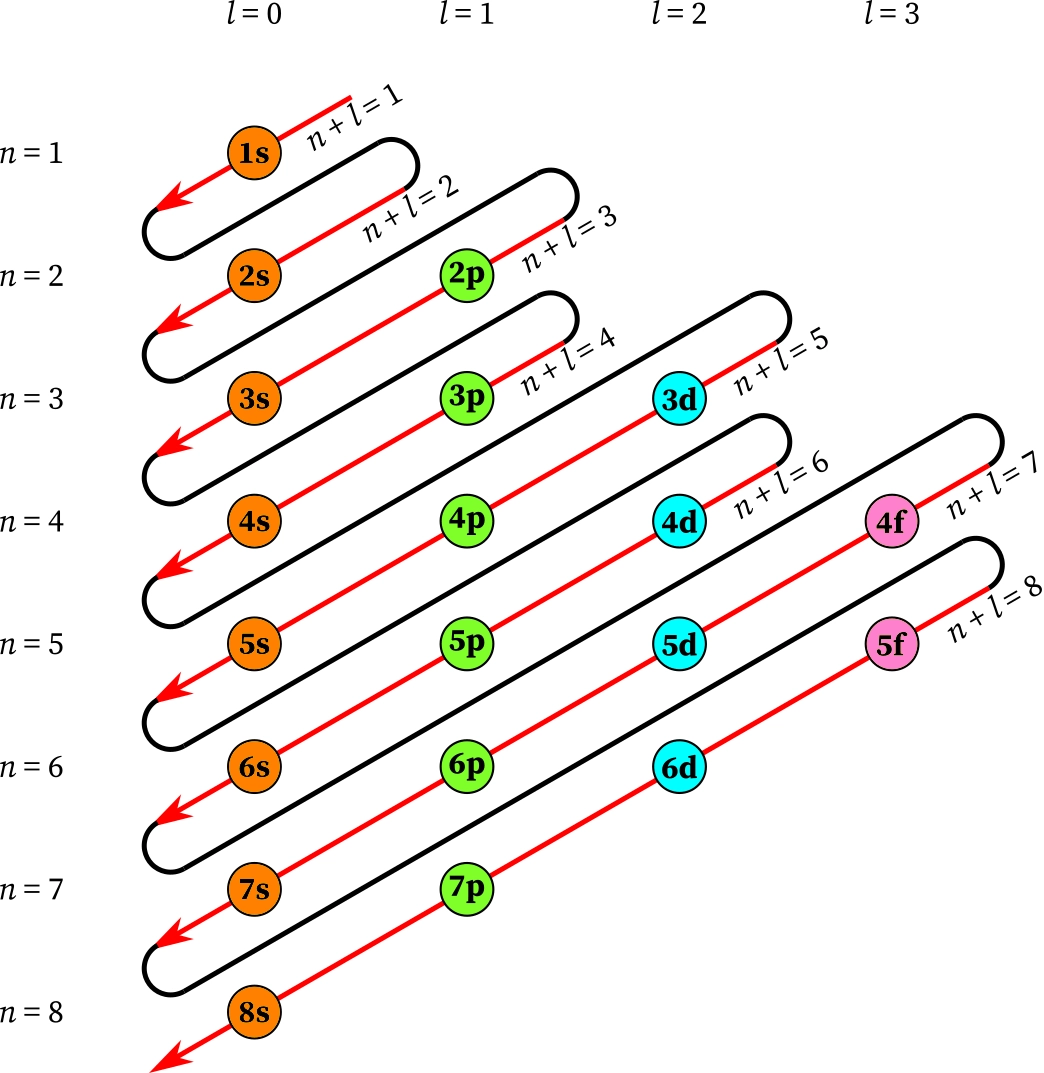
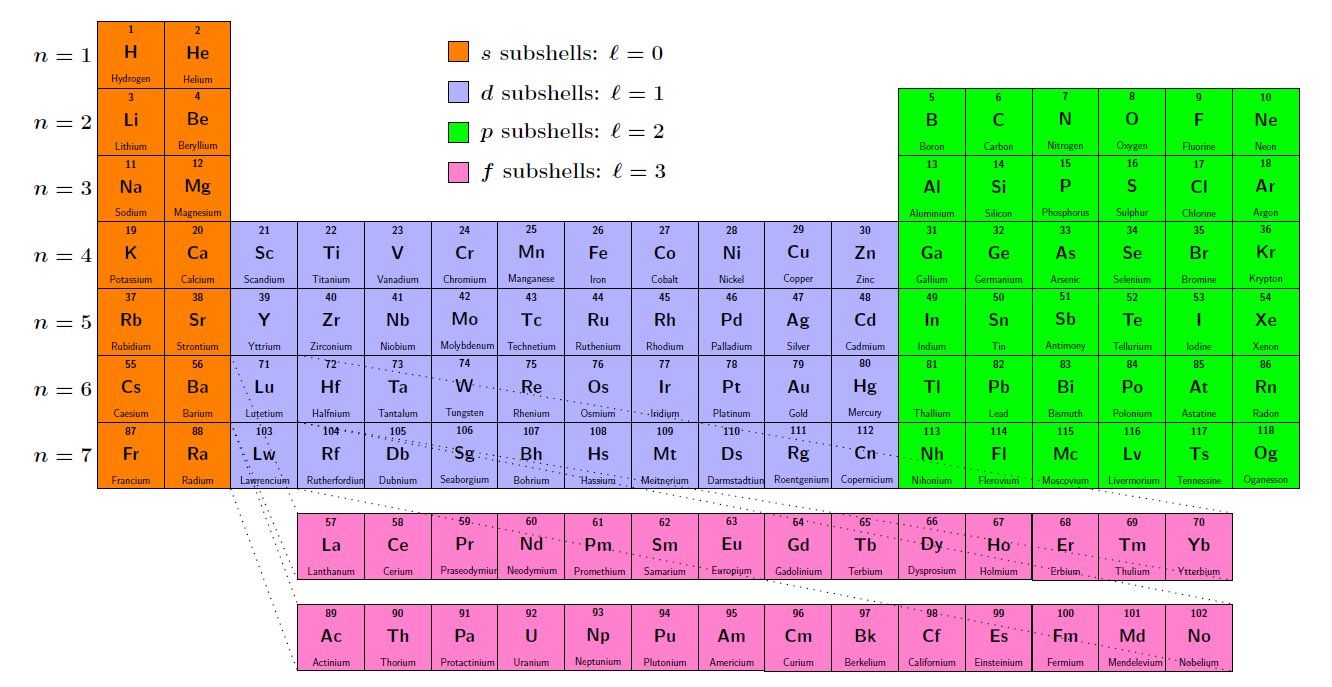
Re: Second Quantization and the Kepler Problem
The correspondence is Fock’s stereographic projection from momentum space. The functor preserves because the hydrogen Hamiltonian commutes with the Runge-Lenz vector. Eigenvalue map: on .