The n-Category Café

Grothendieck’s Galois theory

In 1960 and 1961 Grothendieck developed a new approach to Galois theory in a series of seminars that got written up as SGA1. This is sometimes called Grothendieck’s Galois theory.

His approach was very geometrical. He treated the Galois group of a field $k$ as the fundamental group of a funny sort of ‘space’ associated to that field, called $Spec(k)$. This in turn let him treat sufficiently nice field extensions of $k$ as giving covering spaces of $Spec(k)$.

In short, he was exploiting the duality between commutative algebra and geometry, but pushing it further than ever before! An extension of fields is a map

$$k \to k'$$

from a field $k$ into a bigger field $k'$, but turning around the arrow here, he got a covering space

$$Spec(k') \to Spec(k)$$

Using this idea he was able to generalize Galois theory from fields to commutative rings and even more general things.

In the usual treatment of Grothendieck’s Galois theory the details get technical in ways that may be off-putting to people who aren’t committed to learning algebraic geometry. For example, what sort of ‘space’ is $Spec(k)$? It’s something called a ‘scheme’. How do we define a ‘covering space’ in this context? For that we need to know a bit about ‘Grothendieck topologies’. And so on. It seems we need to either hand-wave or dive into these topics. This is a pity because the underlying ideas are very simple — and among the most beautiful in 20th-century mathematics.

Luckily, a bunch of mathematicians thought about what Grothendieck had done and extracted some of its simple essence. That’s what I want to talk about here! So I won’t talk about algebraic geometry in any serious way, just simpler things.

But to get to these simpler things, it pays to look at a slight glitch in the story I’ve told so far.

I said that nice field extensions of a field $k$ give covering spaces of $Spec(k)$. But they can’t give all the covering spaces of $Spec(k)$, and it’s easy to see why. If we have two covering spaces of some space $X$ we can take their disjoint union and get another covering space. But what does that look like in in the world of algebra? If all covering spaces of $Spec(k)$ came from fields extending $k$, it would mean we could take the product of two fields extending a field $k$ and get another field extending $k$! You see, turning the arrows around in the definition of ‘disjoint union’ we get the definition of ‘product’.

But the product of fields is not usually a field! To include products of fields in our story, we need some more general commutative algebras. So we need to think about these.

They are called ‘commutative separable algebras’. And it turns out that commutative separable algebras over a field $k$ are exactly the same thing as finite products of ‘nice’ field extensions of $k$.

So, to understand Grothendieck’s approach to Galois theory in a simple low-brow way, it’s good to think about commutative separable algebras. But instead of starting by defining them, I want to make you see how inevitable this definition is. And for that, it’s easiest to look at a simpler context where this definition comes up. This will take a while, but it’s very nice math in its own right — and I’ll need it to make sense of the big stew of ideas that’s bubbling away in my brain.

There’s also a conjecture here, that you might help me prove.

Sets versus vector spaces

Every set $X$ gives rise to complex vector space $F(X)$ whose basis is $X$. This is called the free vector space on $X$. Similarly, any function between sets $f \colon X \to Y$ gives a linear map between their free vector spaces, say $F(f) \colon F(X) \to F(Y)$, which sends basis elements to basis elements. We can summarize this, and a bit more, by saying there’s a functor

$$F \colon \mathsf{Set} \to \mathsf{Vect}_{\mathbb{C}}$$

This functor actually embeds the category of sets into the category of complex vector spaces. So it’s very natural to ask: if someone just hands you the category $\mathsf{Vect}_{\mathbb{C}}$, can you find the category $\mathsf{Set}$ sitting inside it?

Since every vector space has a basis, every object of $\mathsf{Vect}_{\mathbb{C}}$ is isomorphic to the free vector space on some set — so there’s nothing much to do there. But not every linear map $\ell \colon V \to W$ comes from a function between sets, no matter how you pick bases for $V$ and $W$. So there really is an interesting question here. It’s the question of how we find set theory lurking inside linear algebra. And this question will lead us inexorably to commutative separable algebras!

Since the category of sets has finite products, every set $X$ comes with a diagonal map

$$\Delta_X \colon X \to X \times X$$

and a unique map to the terminal set

$$!_X \colon X \to 1$$

I like to say that $\Delta_X$ duplicates elements of $X$, while $!_X$ deletes them. If we draw these maps using string diagrams, which we read from the top down, the diagonal $\Delta_X$ looks like this:

$\quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

while $!_X$ looks like this:

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

If you duplicate an element of $X$ you can then duplicate either the first or the second copy, and the result is the same, so

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad$

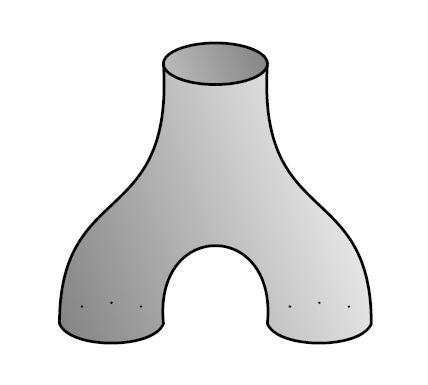
Since this looks like an upside-down version of the associative law, this equation is called the coassociative law. Similarly, if you duplicate an element you can delete either the first or the second copy, and the result is the same as if you’d left that element alone:

$\qquad \qquad \qquad \qquad \qquad \qquad$

These are called the counit laws.

Since all these laws are just the laws for a monoid written upside down, we call $(X,\Delta_X, !_X)$ a comonoid. Following this line of thought, we also call $\Delta_X$ the comultiplication and $!_X$ the counit of this comonoid.

Furthermore, if we duplicate an element of a set and then switch the two copies, it’s the same as if we had just duplicated but not switched:

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

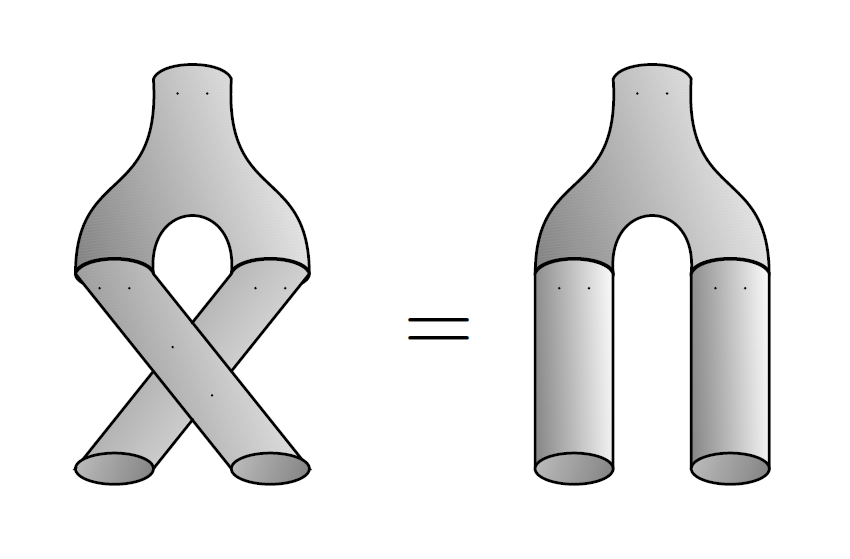
This is called the cocommutative law.

So, all in all, we say every set is a cocommutative comonoid in $(\mathsf{Set}, \times, 1)$.

You can show more: for any category with finite products, every object is a cocommutative comonoid. Even better, it’s a cocommutative comonoid in a unique way! And better still, every morphism between objects is a comonoid homomorphism. That is: if you have a morphism $f \colon X \to Y$, it obeys

$$\Delta_Y \circ f = (f \times f) \circ \Delta_X, \qquad !_Y \circ f = !_X$$

These are fun equations to check if you know category theory. If that’s too hard, at least check them in the category $\mathsf{Set}$. And if that’s too hard, at least draw them in the style of the pictures I’ve been using here.

What does all this have to do with our problem: recognizing when a linear map between vector spaces comes from a function between sets? Well, the functor $F \colon \mathsf{Set} \to \mathsf{Vect}_{\mathbb{C}}$ turns cartesian products into tensor products:

$$F(X \times Y) \cong F(X) \otimes F(Y)$$

so we should expect that it sends any set, which is a cocommutative comonoid in $(\mathsf{Set}, \times, 1)$, to a cocommutative comonoid in $(\mathsf{Vect}_{\mathbb{C}}, \otimes, \mathbb{C})$. And this is indeed true! But we usually call such a thing a cocommutative coalgebra.

Let me say it again a different way. For any set $X$, the vector space $F(X)$ has a basis with one basis vector $e_i$ for each $i \in X$. It becomes a cocommutative coalgebra where the comultiplication

$$\delta \colon V \to V \otimes V$$

just duplicates each basis element:

$$\delta(e_i) = e_i \otimes e_i$$

and the counit

$$\epsilon \colon V \to \mathbb{C}$$

just discards each basis element:

$$\epsilon(e_i) = 1$$

So, our ‘free vector space’ functor $F \colon \mathsf{Set} \to \mathsf{Vect}_{\mathbb{C}}$ sends sets to cocommutative coalgebras. Similarly, it sends functions between sets to coalgebra homomorphisms: linear maps between coalgebras that preserve the comultiplication and counit.

Even better, any coalgebra homomorphism $\alpha \colon F(X) \to F(Y)$ must equal $F(f)$ for some function $f \colon X \to Y$! This is a good thing to check, if you’re sinking under the weight of definitions and want to do something that forces you to understand them.

But there’s a fly in the ointment. Not every cocommutative coalgebra comes from a set in the way I’ve described! There are many others that are not even isomorphic to those coming from sets. For example, if you take any finite-dimensional commutative algebra, its dual vector space is a cocommutative coalgebra.

So, how can we tell which cocommutative coalgebras come from sets? There must be some way to characterize them. And indeed there is!

For starters, if $X$ is a set, we can think of the free vector space $F(X)$ as consisting of functions $f \colon X \to \mathbb{C}$ that are finitely supported: that is, nonzero at just finitely many points. And we can multiply two finitely supported functions in the usual pointwise way, and get another finitely supported function. So, $F(X)$ also has a multiplication

$$m: F(X) \otimes F(X) \to F(X)$$

which we can draw like this:

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

Of course, this multiplication obeys the associative law:

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad$

and the commutative law:

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

It looks like we’re copying all our previous work, only upside-down! But there’s a catch. What about the unit? This should be a map

$$i: \mathbb{C} \to F(X)$$

so we’ll draw it like this:

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

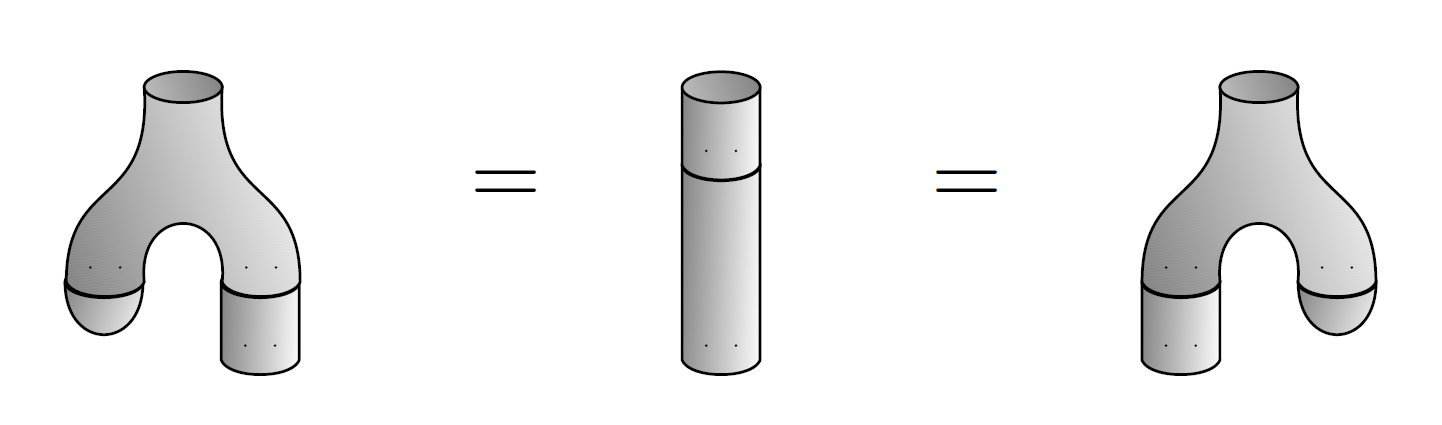
And just as counit obeyed some counit laws, we’d like the unit to obey the unit laws:

$\qquad \qquad \qquad \qquad \qquad \qquad$

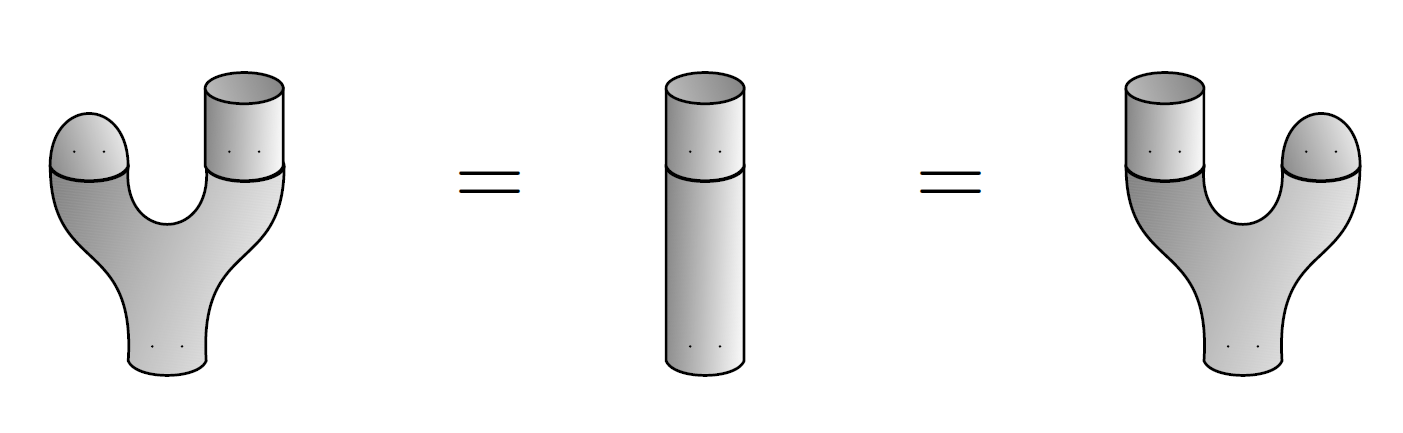
If a vector space has a multiplication and unit obeying the associative, commutative and unit laws, it’s a commutative algebra. You probably knew that, if you’ve survived everything I’ve said so far.

But does such a unit actually exist for our vector space $F(X)$, equipped with the multiplication we gave it? If you think about it, the unit laws force $i(1) \in F(X)$ to be the constant function on $X$ that takes the value $1$ everywhere — since only that function acts as the unit for pointwise multiplication of functions. But remember: in the function picture, $F(X)$ consists of finitely supported functions! So we only get a unit when $X$ is a finite set!

So now we face a choice. We can either pursue our original goal of picking out the category sets and functions as a subcategory of $\mathsf{Vect}_{\mathbb{C}}$, or switch to a new goal: picking out the category of finite sets and functions.

Let’s switch to this new goal for a while. We can do it. And then — it will turn out — we can describe all sets and functions by dropping everything that involves the unit.

So far this is what we’ve seen: if $X$ is a finite set, the vector space $F(X)$ is both a commutative algebra and a cocommutative coalgebra.

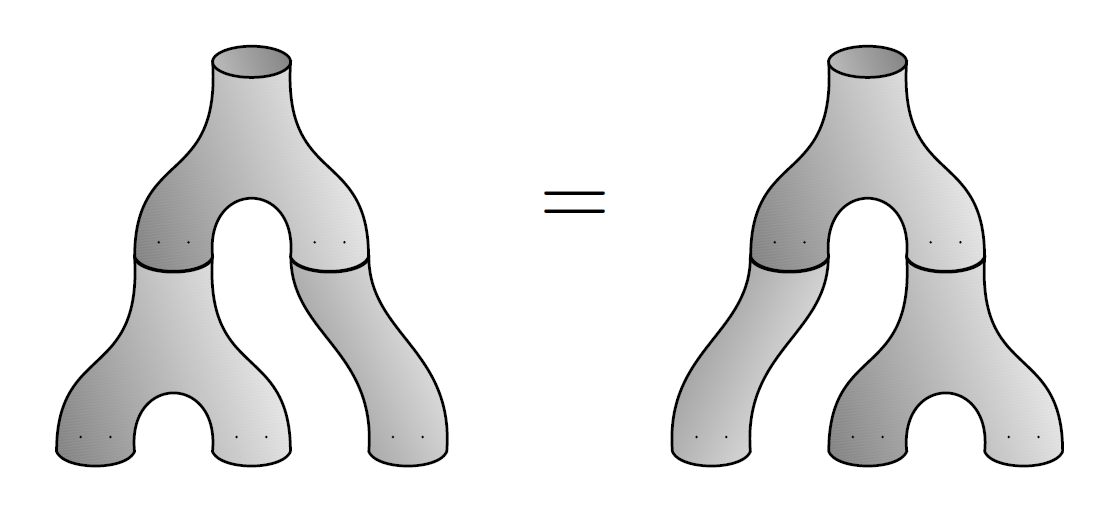
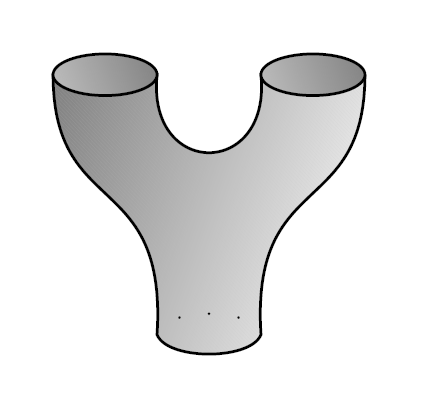
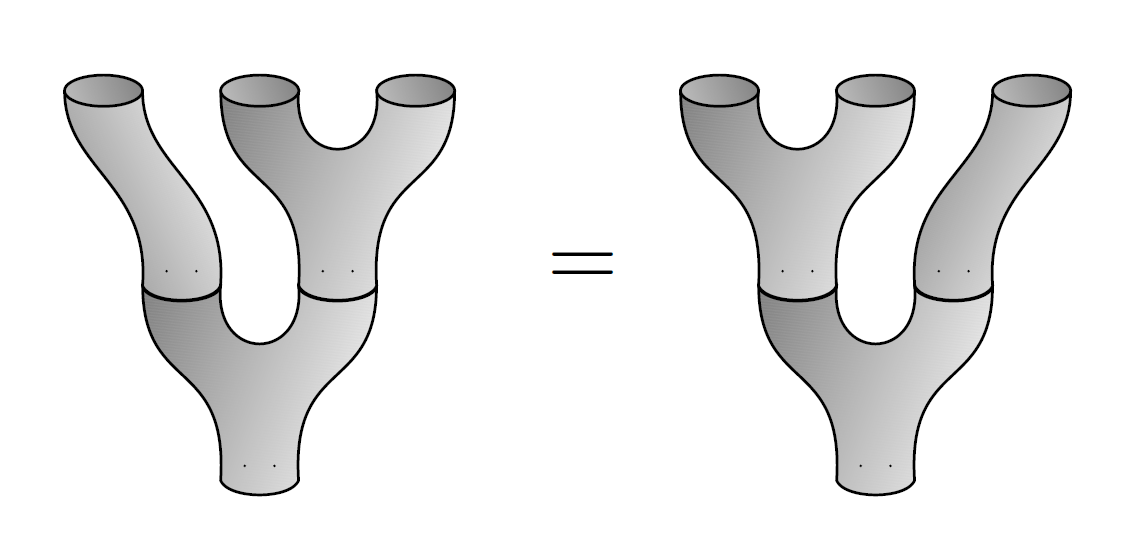
But we’re not done yet, because the multiplication and comultiplication get along. That is, they obey some laws. First, they obey the Frobenius laws:

$\quad \qquad \qquad \qquad \qquad$

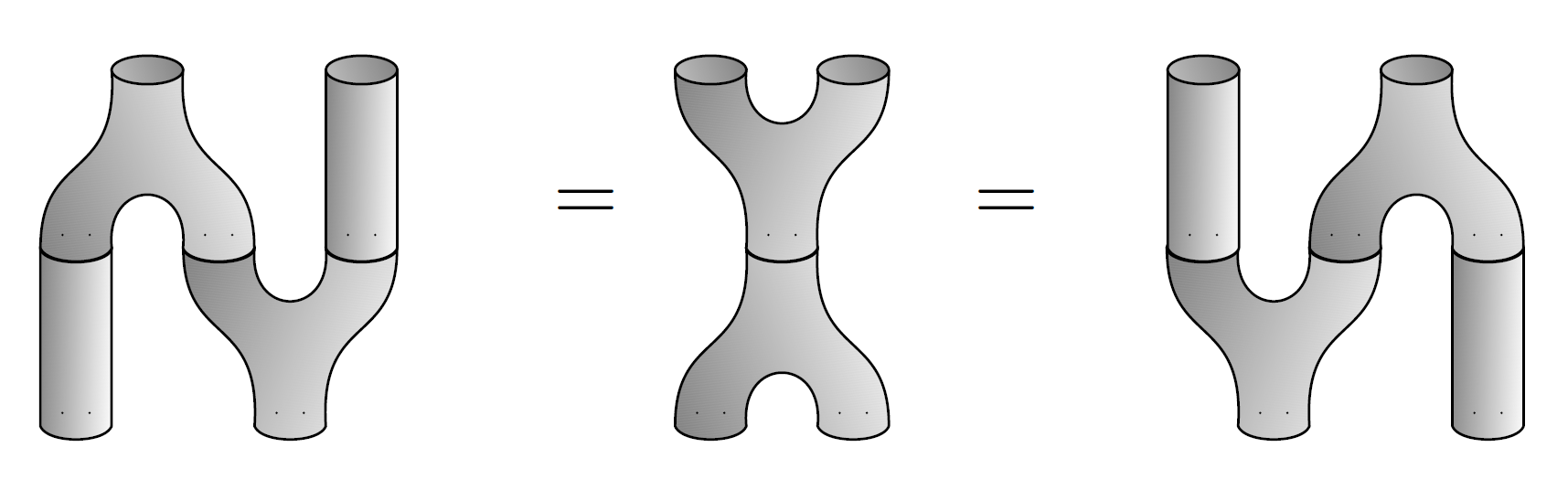
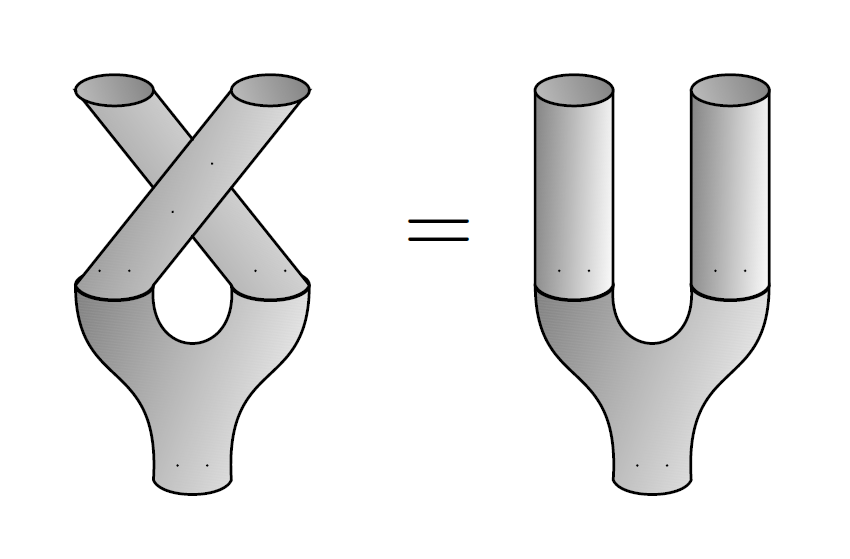
Second, they obey the special law:

$\quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

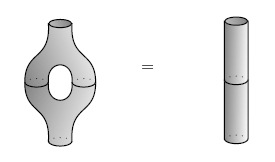
I’ll let you check these things.

A vector space that’s both an algebra and coalgebra and also obeys the Frobenius laws is called a Frobenius algebra. If in addition it obeys the special law, it’s called a special Frobenius algebra. So, we’re seeing that the free vector space on a finite set is a commutative special Frobenius algebra. By the way, a Frobenius algebra is commutative if and only if it is cocommutative — so it’s enough to say “commutative”.

Whew! Are we done yet?

Yes and no. We are done with finding operations and laws. But in fact we’ve gone a bit too far — in a certain very interesting sense. We can define a Frobenius homomorphism of Frobenius algebra to be a map that preserves all the operations: multiplication, unit, comultiplication and counit. So, it’s both an algebra homomorphism and a coalgebra homomorphism. But then something shocking happens: all Frobenius homomorphisms are isomorphisms! There’s a fun proof using string diagrams, which I will let you reinvent.

In fact we can prove this:

Theorem 1. The category of commutative special Frobenius algebras in $\mathsf{Vect}_{\mathbb{C}}$, and Frobenius homomorphisms between them, is equivalent to the category of finite sets and bijections.

We were trying to find the category of sets and functions hiding in the world of linear algebra, but instead we found the category of finite sets and bijections. That’s okay. We just need to back off a bit to drop these restrictions. We can get rid of the bijection constraint like this:

Theorem 2. The category of commutative special Frobenius algebras in $\mathsf{Vect}_{\mathbb{C}}$, and coalgebra homomorphisms between these, is equivalent to the category of finite sets and functions.

To get a feeling for this, think about the unique function from a 2-element set to a 1-element set. Hitting this with our functor $F$ we get a linear map $\mathbb{C}^2 \to \mathbb{C}$. This map is just addition! Check that this map is not an algebra homomorphism, but is a coalgebra homomorphism.

Next let’s get rid of the finiteness constraint. I’ve already hinted at how: drop everything about the unit, since $F(X)$ doesn’t have a unit when $X$ is infinite.

To do this, we need a name for a commutative special Frobenius algebra that could be lacking a unit. Furthermore, to state a result like Theorem 2, we want to think about coalgebra homomorphisms between these things. So we’ll say this:

Definition. A coseparable coalgebra is a coalgebra for which there exists a multiplication that obeys the Frobenius and special laws.

Notice the subtlety: such a multiplication has to exist, but we don’t pick a specific one. So coseparability is a property of a coalgebra, not an extra structure.

All this led me to this guess, but I couldn’t prove it:

Conjecture 3. The category of cocommutative coseparable coalgebras in $\mathsf{Vect}_{\mathbb{C}}$, and coalgebra homomorphisms between these, is equivalent to the category of sets and functions.

Luckily, Theo Johnson–Freyd found a nice proof in the comments below. So we know how set theory sits inside the world of linear algebra! And we’d be done for the day if I were trying to explain coseparable coalgebras. But Grothendieck, like most algebraic geometers, preferred algebras to coalgebras — for good reasons, which I will not explain here.

So, let’s try to dream up an analogue of Conjecture 3 for algebras. Let’s copy our definition of coseparable coalgebra and say this:

Definition. A separable algebra is an algebra for which there exists a comultiplication that obeys the Frobenius and special laws.

This is the definition I’ve been leading up to all this time! And notice: now it’s the comultiplication whose existence is being treated as a mere property, not a structure that needs to be preserved. So, the correct maps between separable algebras are simply algebra homomorphisms.

Now we can state the theorem I’ve been leading up to all this time:

Theorem 4. The category of commutative separable algebras in $\mathsf{Vect}_{\mathbb{C}}$, and algebra homomorphisms between these, is equivalent to the opposite of the category of finite sets and functions.

Hey! Now we just get finite sets again! The reason is that any commutative separable algebra in $\mathsf{Vect}_{\mathbb{C}}$ is isomorphic to $F(X)$ for some set $X$, with the usual pointwise multiplication. But this set must be finite, for the algebra to have its unit.

This could be seen as a flaw if we were aiming to handle infinite sets. But if we want to do that, it seems we should use coalgebras. Grothendieck went with algebras.

Conclusion

I’ve tried to make the theorems here plausible, but they are a bit harder to prove than you might think from what I wrote. In particular, they’re not true if we replace the complex numbers by the real numbers!

In particular, I said that every commutative separable algebra in $\mathsf{Vect}_{\mathbb{C}}$ is isomorphic to the algebra of complex-valued functions on a finite set. But the analogous thing fails in the real case:

Puzzle. Find a commutative separable algebra in $\mathsf{Vect}_{\mathbb{R}}$ that is not isomorphic to the algebra of real-valued functions on a finite set.

Perhaps unsurprisingly, this is connected to Galois theory. I’m talking about Grothendieck’s approach to Galois theory, after all! It turns out that the obvious analogues of Theorems 1, 2, and 4 hold for algebraically closed fields, but not other fields. Next time I’ll talk about what happens for other fields, though you can already guess from what I’ve said so far.

So, what I’ve really been discussing today is Grothendieck’s approach to Galois theory in the degenerate case of algebraically closed fields, where the Galois group is trivial. This is just the tip of the iceberg!

References

Since the theorems I stated are a bit harder than they look, I should give you references to them.

• Aurelio Carboni, Matrices, relations, and group representations, Journal of Algebra 136 (1991), 497–529.

This really digs into the meaning of separable algebras, and I owe a lot of my thoughts to this paper. However, these offer more traditional treatments:

• Frank DeMeyer and E. Ingraham, Separable Algebras Over Commutative Rings, Lecture Notes in Mathematics 181, Springer, Berlin, 1971.

• Timothy J. Ford, Separable Algebras, American Mathematical Society, Providence, Rhode Island, 2017.

To get proofs of what I’m calling Theorems 1, 2 and 4 out of these references, you have to scrabble around a bit. Ultimately it would be much nicer to find clean self-contained proofs, but for now let’s start with Theorem 4.5.7 in Ford’s book, which in my numbering system will be:

Theorem 5. Let $k$ be a field and $A$ a $k$-algebra. Then $A$ is a separable $k$-algebra if and only if $A$ is isomorphic to a finite direct sum of matrix rings $M_{n_i}(D_i)$ where each $D_i$ is a finite dimensional $k$-division algebra such that the center $Z(D_i)$ is a finite separable extension field of $k$.

Since we’re not doing Galois theory yet, let’s see what this says when $k$ is algebraically closed. Then the only division algebra over $k$ is $k$ itself, and the only finite separable extension field of $k$ is $k$ itself, so we get:

Theorem 6. Let $k$ be an algebraically closed field. Then an algebra in $\mathsf{Vect}_k$ is separable if and only if it is isomorphic to a finite product of matrix algebras over $k$.

(A finite product of algebras is the same as what ordinary people call a finite direct sum of algebras, but it is really the product in the category of algebras, not a coproduct.)

We’ll get interested in noncommutative separable algebras later in this series. But in the commutative case things simplify further:

Theorem 7. Let $k$ be an algebraically closed field. Then a commutative algebra in $\mathsf{Vect}_k$ is separable if and only if it is isomorphic to a finite product of copies of $k$.

Any such algebra, let’s call it $k^n$, can be given the structure of a special commutative Frobenius algebra by defining a comultiplication and counit in terms of the standard basis vectors $e_i \in k^n$ as follows:

$$e_i \mapsto e_i \otimes e_i, \qquad e_i \mapsto 1$$

Since any algebra homomorphism $\alpha \colon k^n \to k^m$ must send idempotents in $k^n$ to idempotents in $k^m$, it must send each sum of distinct basis vectors $e_i \in k^n$ to a sum of distinct basis vectors $f_j \in k^m$. It must also send the multiplicative identity of $k^n$, which is the sum of all the $e_i$, to the multiplicative identity in $k^m$, which is the sum of all the $f_j$. Thus we must have

$$\alpha(e_i) = \sum_{j \in f^{-1}(i)} e_j$$

for some function $f \colon \{1,\dots, m\} \to \{1, \dots, n\}$, and any function will do. This shows that the category of commutative separable algebras is equivalent to the opposite of the category of finite sets and functions! We get a slight strengthening of Theorem 4:

Theorem 4$\prime$. Let $k$ be an algebraically closed field. Then the category of commutative separable algebras in $\mathsf{Vect}_k$, and algebra homomorphisms between these, is equivalent to the opposite of the category of finite sets and functions.

We can also state this result in terms of Frobenius algebras, since we have:

Theorem 8. Let $k$ be any field. Then any separable algebra in $\mathsf{Vect}_k$ is finite-dimensional, and can be given a comultiplication and counit making it into a special Frobenius algebra.

The finite-dimensionality follows from Ford’s Theorem 4.5.7 above, and by definition any separable algebra can be given a comultiplication obeying the Frobenius and special laws, so the only news here is that we can then give it a counit obeying the counit laws. This is proved in the first theorem in Section 2 of Carboni’s paper.

This means that the category of (commutative) separable algebras is equivalent to the category of (commutative) special Frobenius algebras and algebra homomorphisms. So, we can restate Theorem 4$\prime$ in this way:

Theorem 4$\prime\prime$. Let $k$ be an algebraically closed field. Then the category of commutative special Frobenius algebras in $\mathsf{Vect}_k$, and algebra homomorphisms between these, is equivalent to the opposite of the category of finite sets and functions.

But it’s not good to say two categories are equivalent without specifying the equivalence, so let’s do that. There’s a functor

$$k^- \colon \mathsf{FinSet}^{\mathrm{op}} \to \mathsf{FinVect}_k$$

where $\mathsf{FinVect}_k$ is the category of finite-dimensional vector spaces over $k$. This functor maps each finite set $X$ to the vector space $k^X$ of $k$-valued functions on $X$. That vector space becomes an algebra with pointwise multiplication and a coalgebra with the comultiplication and counit we’ve seen:

$$e_i \mapsto e_i \otimes e_i, \qquad e_i \mapsto 1$$

and these fit together to form a commutative special Frobenius algebra. Putting everything together we get:

Theorem 4$\prime\prime\prime$. Let $k$ be an algebraically closed field. Then the functor

$$k^- \colon \mathsf{FinSet}^{\mathrm{op}} \to \mathsf{FinVect}_k$$

gives an equivalence between $\mathsf{FinSet}^{\mathrm{op}}$ and the category of commutative special Frobenius algebras and algebra homomorphisms between these.

Note the latter is equivalent to the category of commutative separable algebras.

We can get rid of the ‘opposite’ business using vector space duality: taking duals gives an equivalence between the category of finite-dimensional vector spaces and its opposite. Composing this with the above functor we get a functor

$$(k^-)^\ast \colon \mathsf{FinSet}^{\mathrm{op}} \to \mathsf{FinVect}_k^{\mathrm{op}}$$

sending any finite set $X$ to the dual of the vector space of $k$-valued functions on $X$. But this in turn gives a functor from $\mathsf{FinSet}$ to $\mathsf{FinVect}_k$, and that’s just our old friend the free vector space functor, restricted to finite sets:

$$F \colon \mathsf{FinSet} \to \mathsf{FinVect}_k$$

Taking the dual maps commutative special Frobenius algebras to commutative special Frobenius algebras, switching the multiplication and unit with the comultiplication and counit. Thus we get Theorem 3, which I’ll state more precisely now:

Theorem 3$\prime$. Let $k$ be an algebraically closed field. Then the functor

$$F \colon \mathsf{FinSet} \to \mathsf{FinVect}_k$$

gives an equivalence between $\mathsf{FinSet}$ and the category of commutative special Frobenius algebras and coalgebra homomorphisms between these.

Finally, let’s restrict $F$ to the category $\mathsf{FinBij}$ of finite sets and bijections. Clearly $F$ maps these to isomorphisms. But by my explicit description of all the algebra homomorphisms $\alpha \colon k^n \to k^m$, we see every isomorphism of these comes from a bijection $f \colon \{1,\dots, m\} \to \{1, \dots, n\}$. So, we get this more precise version of Theorem 1:

Theorem 1$\prime$. Let $k$ be an algebraically closed field. Then the functor

$$F \colon \mathsf{FinSet} \to \mathsf{FinVect}_k$$

gives an equivalence between $\mathsf{FinSet}$ and the category of commutative special Frobenius algebras and Frobenius algebra homomorphisms between these (which are all isomorphisms).

The fact that all homomorphisms of Frobenius algebras are isomorphisms is Lemma 2.4.5 here:

• Joachim Kock, Frobenius Algebras and 2D Topological Quantum Field Theories, Cambridge University Press, Cambridge 2004.