Lie oo-Connections and their Application to String- and Chern-Simons n-Transport
Posted by Urs Schreiber
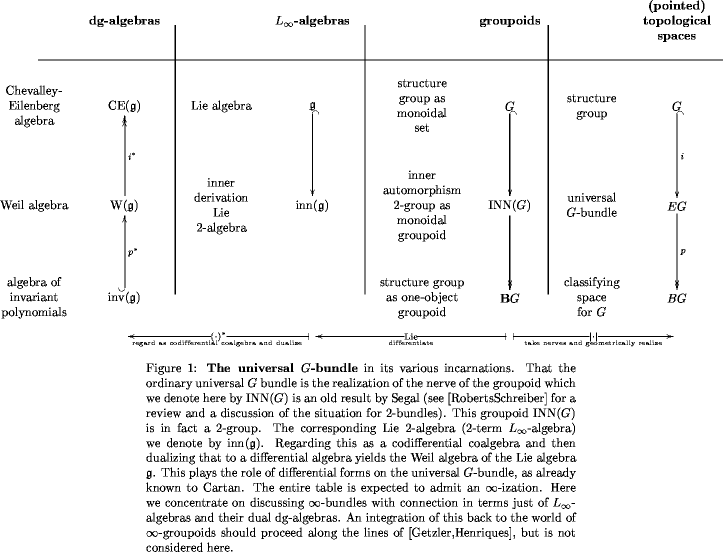
Hisham Sati, Jim Stasheff and myself are working on writing up some ideas on Lie -algebra cohomology and its application to String- and Chern-Simons -Transport, further exploring the second edge of the cube.
We would like to share this document:
H. Sati, J. Stasheff, U. S.
-algebra connections and applications to String- and Chern-Simons -Transport
arXiv:http://arxiv.org/abs/0801.3480
(pdf of the latest version)
This consists of three parts:
Part A : Overview and physical applications
Part B: Lie -algebras, their cohomology and their String-like extensions
Part C: Categorified Cartan-Ehresmann connections and lifts through String-like extensions.
This can be thought of as providing details to the discussion provided in my slide show String- and Chern-Simons -Transport. -Café regulars will recognize a certain synthesis of topics I used to discuss here, like inner automorphism -groups, String and Chern-Simons Lie -algebras, -Curvature , obstruction theory and other things. To some extent, the main idea here found its final form after John posed a nice problem in Higher Gauge Theory and Elliptic Cohomology.
Much progress on the relation of the general formalism to (heterotic) string theory and supergravity/M-theory occurred when I visited Hisham Sati in Yale. The full implications are only briefly indicated here.
We’d be grateful for whatever comment you might have.
Math abstract. We give a generalization of the notion of a Cartan-Ehresmann connection from Lie algebras to -algebras and use it to study the obstruction theory of lifts through higher String-like extensions of Lie algebras.
Physics abstract. It is known that over a D-brane the Kalb-Ramond field restricts to a 2-bundle with connection (a gerbe) which can be seen as the obstruction to lifting the -bundle on the D-brane to a -bundle. We discuss how this phenomenon generalizes from the ordinary central extension to higher categorical central extensions, like the String-extension . Here the obstruction to the lift is a 3-bundle with connection (a 2-gerbe): the Chern-Simons 3-bundle classified by the first Pontrjagin class. For this obstructs the existence of a String-structure. We discuss how to describe this obstruction problem in terms of Lie -algebras and their corresponding categorified Cartan-Ehresmann connections. Generalizations even beyond String-extensions are then straightforward. For the next step is “Fivebrane structures” whose existence is obstructed by certain generalized Chern-Simons 7-bundles classified by the second Pontrjagin class.
Statement of the main results
We define, for any -algebra and any smooth space , a notion of
-descent objects over ;
and an extension of these to
-connection descent objects over .
These descent objects are to be thought of as the data obtained from locally trivializing an -bundle (with connection) whose structure -group has the Lie -algebra .
We define for each -algebra a dg-algebra of invariant polynomials on .
We show that every -connection descent object gives rise to a collection of deRham classes on : its characteristic classes. These are images of the cohomology of .
Two descent objects are taken to be equivalent if they are concordant in a natural sense.
Our first main result is
Theorem. Characteristic classes indeed characterize -descent objects in the following sense:
- Concordant -connection descent objects agree in cohomology and have the same characteristic classes.
- Two -descent objects with the same characteristic classes agree in cohomology.
- If two -descent objects differ in cohomology, they are not concordant and cannot have the same characteristic classes.
Remark. We expect that this result can be strengthened. Currently our characteristic classes are just in deRham cohomology. One would expect that these are images of classes in integral cohomology which completely characterize equivalent -descent objects. While we do not attempt here to discuss integral characteristic classes in general, we discuss some aspects of this for the case of abelian Lie -algebra by relating -descent objects to Deligne cohomology.
We define String-like extensions of -algebras coming
from any -algebra cocycle : a closed element in the
Chevalley-Eilenberg dg-algebra corresponding to : .
These generalize the String Lie 2-algebra which governs the dynamics
of (heterotic) superstrings.
Then we do this and that and arrive at our second main result:
Theorem. For any degree -cocycle that transgresses via to an invariant polynomial , the obstruction to lifting a -descent object to a -descent object is a -descent object whose single characteristic class is the class corresponding to of the original -descent object.
We discuss the following applications.
- For an ordinary semisimple Lie algebra and its canonical 3-cocycle, this says the obstruction to lifting a -bundle to a String 2-bundle is a Chern-Simons 3-bundle. The vanishing of this obstruction is known as a String structure.
- This result generalizes to all String-like extensions. Using the 7-cocycle on we obtain lifts through extensions by a Lie 6-algebra, which we call the Fivebrane Lie 6-algebra. Accordingly, fivebrane structures are obstructed by the second Pontrjagin class and are related to higher twists in string theory.
- This pattern continues and one would expect our obstruction theory for lifts through string-like extensions with respect to the 11-cocycle on to correspond to Ninebrane structure.
The issue of -brane structures for higher was discussed before in [MickelssonPercacci]. In contrast to the discussion there, we here see -brane structures only for , corresponding to the list of invariant polynomials and cocycles for .
- We discuss how the action functional of the topological field theory known as BF-theory arises from the invariant polynomial on a strict Lie 2-algebra, in a generalization of the integrated Pontrjagin 4-form of the topological term in Yang-Mills theory.
This is similar to but different from the Lie 2-algebraic interpretation of BF theory indicated in [GirelliPfeifferPopescu], where the “cosmological” bilinear in the connection 2-form is not considered and a constraint on the admissable strict Lie 2-algebras is imposed.
- We discuss the parallel transport induced by a -connection, relate it to the -functorial parallel transport and point out how this leads to -model actions in terms of dg-algebra morphisms. This makes contact with the corresponding BV-formalism, though the details of that are not discussed here.

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport
Does this work tell us anything about all those dualities (S, T, U, etc.) between string theories?